
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б.а.о. и их св-ва (коммут-ть, ассоц-ть, нейтральный эл-т, симметричный эл-т).Стр 1 из 5Следующая ⇒
Б.а.о. и их св-ва (коммут-ть, ассоц-ть, нейтральный эл-т, симметричный эл-т). Пусть G-непустое мн-во. Бинарной алгебраической операцией наз. некоторое отображение из дек. отображения f:GxG->G. Обозн.g1og2. Форма записи б.а.о. аддитивная и мультипликативная. При аддитивной ф.з. – операция сложения (g1+g2). При мультипликативной – умножение (g1*g2). Пример. R: +,*,- б.а.о.; / не явл.б.а.о. на R. N: +,*; -,/ не явл.б.а.о. на N. R*=R\{0}: / б.а.о. V3: +,-,* P(A) – мн-во всех подмн-в мн-ва А: U,∩,\. Если на мн-ве определена б.а.о. (общий знак o), то обозн. <A, o> и говорят, что композиция определяет на А алгебраическую стр-ру, или что <A, o> - алгебр.стр-ра (алгебр. с-ма). Б.а.о. на мн-ве А наз. ассоциативной, если для Замечание. Св-ва ассоц-ти и коммут-ти независимы: · на мн-ве матриц (АВ)С = А(ВС), но АВ ≠ ВА. · Z: n*k = -n-k, k*n = -k-n, (1*2)*3 = -(-1-2)-3 = 0, 1*(2*3) = -1-(-2-3) = 4. Эл-т е?A наз. нейтральным относительно б.а.о. o на А, если Замечание. Если задана мультипликативная стр-ра, то нейтр.эл-т наз. единицей, если аддитивная, то нулем. Св-во1: Если в алгебр.стр-ре есть нейтр.эл-т, то он единственный. Д-во: (от противного) Пусть ᴲе1,е2: е1 oе2 =е1, е1o е2 =е2 => е1=е2. Эл-т b?A наз. симметричным эл-ту а?A, если a o b = b o а=е. Замечание. 1)Если b сим-ный к а, то а сим-ный к b. 2)Если алгебр.стр-ра аддитивная, то сим-ный эл-т наз. противоположным, если мультипликативная – обратным. Св-во2: Пусть <A, o> ассоц. алгебр. стр-ра с нейтр.эл-том е, тогда Д-во: Пусть b1,b2 – 2 сим-ных эл-та к а. тогда (b1 o a) o b2 = e o b2 = b2 ð b1=b2 b1 o (a o b2) = b1 o e = b1
Теорема о независимости результата ассоциативной б.а.о. от расстановки скобок. Теорема. Если б.а.о. на А ассоц-на, то рез-т ее последовательного применения к n эл-там мн-ва А не зависит от расстановки скобок. Д-во: ММИ по n. Если n=1 д-ть нечего. n=2 - д-ть нечего. n=3 => из св-ва ассоц-ти. … n=k – предположим, что вып-ся. n=k+1: · (a1 o а2 o … o аk) o аk+1 · (a1 o … o аm) o ((am+1 o … o аk) o ak+1) a1 o … o аm o am+1 o … o аk o ak+1
Степень элемента и ее свойства. Таблица Кэли. Определение группы и ее свойства. Если на множестве А определена ассоциативная операция умножения, то можно определить степени эл-та а
Свойства: Пусть <А, 1. 2. Если А={
4.Подгруппа: определение и примеры. Критерий подгруппы. Не пустое множество G с определенной на нем б.а.о. называется группой, если: 1. 2. 3. Примеры. <R, +>- группа; <R,×>-не группа, нет обратного; Если операция в группе коммутативна, то группа наз. коммутативной или абелевой. Замечание. Если операция на группе задается как произведение, то группа наз. мультипликативной, элемент е наз. 1; симметрический эл-т к а называется обратным к а, а элемент наз. обратимым. (+)-аддитивная, e - нуль, симметрический - противоположным. Свойства: Если G - мультипликативная группа, то 1. в G существует единственная единица; 2. каждый эл-т а?G имеет единственный обратный [ 3. уравнение ах=b,где Пусть H Замечание. Тривиальные подгруппы G и {e}. Критерий подгруппы. Подмножество H мультипликативной группы G является подгруппой т.и.т.т. когда выполняются следующие условия: 1. 2. 3. Примеры групп. <Z[x], +>; <Q[x], +>; < 5. Гомоморфизм групп: определение и примеры. Ядро гомоморфизма и его свойства. Изоморфизм групп, определение и примеры. Даны две группы <G1, ʘ>, <G2, *>. Отображение f:G1→G2 наз. гомоморфизмом, если это отображение сохраняет операцию, т.е. f(aʘb)=f(a)*f(b), Примеры: 1. Рассм. f: <R*;*> -> <{±1}; *>: a→ Ker f ={a 2. Рассм. g:GLn(R)→R*:A→det A. g(AB)=det(AB)=detAdetB=g(A)g(B) Ker g = SLn(R) Прообраз 1 при гомоморфизме f:G1→G2 наз. ядром гомоморфизма и обозн. Ker f. Свойства гомоморфизма: 1. Если f:G1→G2 - гомоморфизм, то f(G1)<f(G2) = Im G1 = Im G1 2. Если f:G1→G2 гомоморфизм, то f(e1)=e2, f(a-1)=f(a)-1 Отображение f:G1→G2 наз. изоморфизмом, если f – биекция (взаимно однозначное отображение), f – гомоморфизм.
Пример. f:<Z;+>→<2Z;+>:a→2a.
6. Кольцо: определение, примеры, простейшие свойства. Делители нуля и обратимые элементы в кольце: определение, примеры. Кольцом наз. мн-во К с двумя заданными на нём б.а.о.: сложением и умножением, удовлетворяющими след. св-вам: 1. <K; +> - абелева группа (коммутативная); 2. a(bc)=(ab)c, 3. законы сложения и умножения связаны законом дистрибутивности: a(b+c)=ab+ac, (a+b)c=ac+bc, Примеры: 1. Числовые кольца: <Z;+;*> < <Q;+;*> < <R;+;*> < <C;+;*> 2. Полиномиальные кольца: <Z[x];+;*> < <Q[x];+;*> < <R[x];+;*> < <C[x];+;*> 3. <Z[x1];+;*> < <Z[x1, х2];+;*> < …. 4. <Z[x1, х2, …, хn];+;*> < <Q[x1, х2, …, xn];+;*> … 5. Кольцо симметрических полиномов: Sn[x1, …, xn] 6. Матричные кольца: <Mm×n(Z); +;*> < < Mm×n(Q); +;*> Простейшие свойства колец: 1) a(b1+b2+…+bn)=ab1+ab2+…+abn 2) (a1+a2+…+an)b=a1b+a2b+…+anb 3) a(b-c)=ab-ac 4) (a-b)c=ac-bc 5) 6) a*0=0*a=0 7) (-a)b=a(-b)=-ab Делителями нуля наз. такие элементы a, b Примеры: 1. <Z;+;*> -- без делителей нуля. 2. <M2×2(Z);+;*> -- с делителями нуля
Замечание. Обратимый элемент кольца не может быть делителями нуля.
7. Группа К* обратимых элементов кольца К. Утверждение. Если К кольцо с 1, то множество К* с обратимым элементом кольца К является мультипликативной группой. Док-во: Проверим сначала, что операция «*» -есть отображение с операцией на множестве К*,т.е. для любых элементов a,b Рассмотрим а-1b-1 элементов К обратимых b и а:
Доказано!
8. Подкольцо: определение, примеры, критерий подкольца. Пусть К2cК1. К2 – наз. подкольцом, если К2 является кольцом относительно операций, заданных на К1. Теорема(критерий подкольца). Подмножество К2 кольца К1 является подкольцом ó когда вып-ся след.: 1. К2 2. Если a,b 3. Если a,b 9.Гомоморфизмы и изоморфизмы колец: определение, примеры. Ядро гомоморфизма как идеал кольца. Важнейший пример гомоморфизма колец Отображение 1) f(a+b)=f(a) 2) f(a+b)=f(a) Изоморфизм – это такой гомоморфизм, который является биекцией. Пусть К и К’- кольца. Отображение
Если - биекция, то Пример1: Пример2: Пример3: Опр. Пусть
Теорема. Ядро гомоморфизма Теорема (важнейший пример гомоморфизма). Пусть К-кольцо, I-идеал кольца К, тогда отображение Замечание: Идеалы кольца – это ядро его гомоморфизма. Теорема: Если
10. Поле: определение, примеры и простейшие свойства (нет делителей 0, уравнение Коммутативное кольцо с 1, в котором не меньше 2-х элементов называется полем, если любой не нулевой элемент в нем обратим. Не пустое подмножество P1 поля P называется подполем поля P, если оно является полем относительно операций «+» и «*» поля P. Теорема (критерий подполя). Не пустое подмножество P1 поля P, в котором не меньше двух элементов является подполем поля P ó выполняются следующие условия:
1) 2) Пример1:
Док-во. 1*1=1 Пример3: Док-во. · Ком.умнож следует из ком. R; Ед.:
Пример4: Какое из множеств является полем относительно «+» и «*»? 1) mZ –множество целых чисел, кратных m нет 2) 3) 4) 5) 6) 7) Замечание: Поле-это кольцо в котором не нулевые элементы образуют группу. Это группа называется мультипликативной группой поля. Пример. Замечание: Поле P изоморфно Имеет ли смысл говорить о гомоморфизме полей? Замечание: В поле нет делителей нуля. Для Свойства полей: Пусть P-поле, 1) 2) 3) 4) 5) 6) 7)
11. Поле дробей области целостности: построение, примеры, теорема. Пусть К – коммутратвное кольцо с единицей без делителей нуля. На мн-ве пар
Д-во: Рефлексивность, симметричность очевидна. Транзитивность:
Введённое отношение явл. отношением эквивалентности. Класс эквивалентности, который содержит пару Определим операции сложения и умножения дробей по правилу:
Введённые операции над дробями определены корректно, т.е. не зависят от выбора представителей класса эквивалентности. Теорема. Q(K) относительно введённых операций явл. полем. Это поле называется полем дробей области целостности К. Д-во: <Q(K), +> -- абелева группа, асс., ком.,
Дистрибутивность Ед.: Обр. эл.
Примеры: 1) Поле дробей кольца Z целых чисел - есть поле Q рациональных чисел. 2) Поле дробей кольца полиномов P[x] над полем Р от одной переменной наз. полем рац. функций над полем Р и обозначается P[x]
3) Поле дробей над кольцом полиномов от n переменных над полем Р наз. полем рациональных функций от n переменных над полем Р и обозначается P[x1, x2, …,xn ]. 12. Левые и правые смежные классы группы по подгруппе: определение, примеры и свойства (утверждения 1 – 3). Пусть H подгруппа группы G,
Каждый эл-т смежного класса наз. представителем этого класса. Примеры. 1. Левые смежные классы GLn(R) по подгруппе SLn(R) состоят из матриц [|B*A|=|B|*|A|=|B|,
2. Левые смежные классы аддитивной группы Z по подгруппе mZ ( Утверждение 1. Семейство левых (правых) смежных классов группы G по подгруппе H образует разбиение группы G. Утверждение 2. Пусть H подгруппа группы G, 1) Элементы a и b принадлежат одному смежному классу группы G по подгруппе H. 2) aH=bH 3) 4) Утверждение 3. Пусть H подгруппа группы G, тогда соответствие
13. Индекс подгруппы: определение, примеры. Теорема Лагранжа. Нормальные подгруппы: определение, примеры и простейшие свойства. Мощность (число) различных левых смежных классов гр. G по подгруппе Н наз. индексом подгр. Н гр. G и обозначается |G:H|. Пример. |Z: mZ|=m Теорема Лагранжа. Пусть n - порядок гр. G [|G|=n], k порядок подгруппы Н [|H|=k], j индекс H в G [j=|G:H|], тогда n=k*j. Следствие. Если группа G конечная, то порядок подгруппы конечной группы явл. делителем порядка группы. Подгруппа Н группы G наз. нормальной подгруппой (нормальным делителем), если Примеры. 1. Тривиальные нормальные подгруппы группы G: G, {e} 2. S Ln(ℝ) Утверждение. Следующие условия эквивалентны: 1. Н ⊲ G 2. a-1Ha = H Утверждение. Пусть Н ⊲G, пусть a,b 1)aH * bH = (ab)H 2)aH*H = H*aH = H 3)a-1H*aH = aH* a-1H = H Опр. Множество смежных классов группы G по нормальной подгруппе Н будет обозначаться Утверждение. Множество смежных классов
14.Фактор-группа: определение и примеры. Основная теорема о гомомрфизмах групп ( f:G -> G/H ). Канонический гомоморфизм: определение и примеры. Группа G явл. фактор-группой группы G по нормальной подгруппе Н. Пример. Фактор-группа Z/mZ={ 0+mz 1+mz m-1+mz Теорема. Пусть Н - норм.подгр. гр.G и Этот гомоморфизм наз. естественным (каноническим). Замечание. Т.обр., в каждой нормальной подгр. Н гр. G соотв-т гомоморфизм f, ядром которого явл. эта норм.подгр. Пример. Z -> Z/mZ: m->
Замечание. 1) Примерами полей положительной хар-ки явл. все конечные поля, т.е. поля которые состоят из конечного числа эл-ов. Но существуют и бесконечные поля,которые имеют положительную характеристику. 2) Теорема. Если поле Р имеет хар-ку р>0,то р-простое число. Док-во. (от противного) Из рав-ва р=s*t,где s<p, t<p⇒ (s*1)(t*1)=st*1=p*1=0,но в поле нет делителей 0,поэтому s*1=0 или t*1=0.Противоречие. Свойства 1. а) если хар-ка поля Р=р, то б) если р=0, то а) char P=p, пусть n=p* б) char P=0, то из n*a=(n*1)* char P=0⇒n=0-противоречие. 2. Если char P=p, то
Док-во. ММИ по n. n=1:
Значит, Пусть утверждение верно при n=k-1. n=k: Следствие. Если характеристика Р=р, то
20. Пересечение подполей как подполе поля. Простое поле: определение, примеры, Изоморфизм простого подполя Св-во 1. Если Р поле, Р1,Р2 – подполя поля Р, тогда Р1∩ Р2 – подполе поля Р. ►1) 0 и 1 поля Р содержаться и в Р1 и в Р2 (по определению подполя)⇒0 и 1 2.) а) Рассмотрим 2 этапа a и b b) Следствие. Пересечение Рi (i Опр. Поле в котором нет не одного собственного подполя, наз простым. Св-во 2. Q, Zp- простые поля. Теорема. В произвольно поле Р содержится ровно 1 или ровно одно подполе Р: 1) если char P=0, то Р0 изоморфно Q. 2)если char P=р, то Р0 От противного если бы
u(x) Возьмем x=a: u(a) u(a)
t=h(a)
29. Теорема об избавлении от иррациональности в знаменателе дроби: единственность. Построение поля Теорема: Пусть Д-во: единственность Пусть t=h(a) t= deg h(x) deg тогда а - корень полинома h(a)- возможны два случая: если [ Противоречие: т.к. а – алгебраический элемент степени n над F и степень полинома наименьшей степени над F корнем которого является а= n] Следствие 1: Пусть E [то есть степень ровна степени min полинома элемента а надF,другими словами векторы 1,а,…, Д-во: Т. обр. каждый элемент из F(a) имеет вид:
=> - Допустим Это значит, что a- корень полинома f(x)= f(a)=0,но f(x) Конец док-ва. Д-во. n=2 Утверждение верно по следствию 3. Допустим, что это утверждение верно для n-1.
Доказано! Шаги построения. 1) Построить прямоугольный треугольник с катетами 1 и 2, его гипотенуза = 2) Уменьшить на 1 гипотенузу этого треугольника. Получим 3) Поделим полученный отрезок на 4 части. 4) Рисуем окружность единичного радиуса. 5) От начала координат отложить на оси Ох отрезок 6) Строим перпендикуляр 7) Находим ещё 3 оставшиеся вершины с помощью циркуля отлаживая получившуюся дугу окружности. Б.а.о. и их св-ва (коммут-ть, ассоц-ть, нейтральный эл-т, симметричный эл-т). Пусть G-непустое мн-во. Бинарной алгебраической операцией наз. некоторое отображение из дек. отображения f:GxG->G. Обозн.g1og2. Форма записи б.а.о. аддитивная и мультипликативная. При аддитивной ф.з. – операция сложения (g1+g2). При мультипликативной – умножение (g1*g2). Пример. R: +,*,- б.а.о.; / не явл.б.а.о. на R. N: +,*; -,/ не явл.б.а.о. на N. R*=R\{0}: / б.а.о. V3: +,-,* P(A) – мн-во всех подмн-в мн-ва А: U,∩,\. Если на мн-ве определена б.а.о. (общий знак o), то обозн. <A, o> и говорят, что композиция определяет на А алгебраическую стр-ру, или что <A, o> - алгебр.стр-ра (алгебр. с-ма). Б.а.о. на мн-ве А наз. ассоциативной, если для Замечание. Св-ва ассоц-ти и коммут-ти независимы: · на мн-ве матриц (АВ)С = А(ВС), но АВ ≠ ВА. · Z: n*k = -n-k, k*n = -k-n, (1*2)*3 = -(-1-2)-3 = 0, 1*(2*3) = -1-(-2-3) = 4. Эл-т е?A наз. нейтральным относительно б.а.о. o на А, если Замечание. Если задана мультипликативная стр-ра, то нейтр.эл-т наз. единицей, если аддитивная, то нулем. Св-во1: Если в алгебр.стр-ре есть нейтр.эл-т, то он единственный. Д-во: (от противного) Пусть ᴲе1,е2: е1 oе2 =е1, е1o е2 =е2 => е1=е2. Эл-т b?A наз. симметричным эл-ту а?A, если a o b = b o а=е. Замечание. 1)Если b сим-ный к а, то а сим-ный к b. 2)Если алгебр.стр-ра аддитивная, то сим-ный эл-т наз. противоположным, если мультипликативная – обратным. Св-во2: Пусть <A, o> ассоц. алгебр. стр-ра с нейтр.эл-том е, тогда Д-во: Пусть b1,b2 – 2 сим-ных эл-та к а. тогда (b1 o a) o b2 = e o b2 = b2 ð b1=b2 b1 o (a o b2) = b1 o e = b1
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 258; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.82.167 (0.232 с.) |
 a,b,c?A (a o b) o c = a o (b o c). Б.а.о. наз. коммутативной, если
a,b,c?A (a o b) o c = a o (b o c). Б.а.о. наз. коммутативной, если  А
А  =а
=а  (n раз) n
(n раз) n  > ассоциативная алгебраическая структура, тогда для
> ассоциативная алгебраическая структура, тогда для  а
а  ;
; ;
;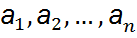 } – конечное мн-во, то б.а.о.
} – конечное мн-во, то б.а.о.  на А можно задать с помощью таблицы Кэли
на А можно задать с помощью таблицы Кэли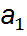


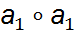





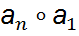




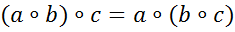 ассоциативность;
ассоциативность;
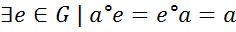 нейтральный элемент;
нейтральный элемент;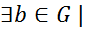 a°b=b°a=e обратимый элемент;
a°b=b°a=e обратимый элемент; ];
];
 ]
] , если H является группой относительно операций, определенных в G (рассматриваются ограничения операции в G на H), то H наз. подгруппой G.
, если H является группой относительно операций, определенных в G (рассматриваются ограничения операции в G на H), то H наз. подгруппой G.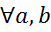
 ab
ab 


 >; GLn(Q)={A
>; GLn(Q)={A  }; SLn(Q)={A
}; SLn(Q)={A  }
} G1
G1
 } – группа
} – группа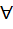 a, b, c
a, b, c 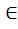 K (ассоц.)
K (ассоц.) N a*nb=na*b=n(ab)
N a*nb=na*b=n(ab)
 К*: ab
К*: ab 

 a – b
a – b 
 наз. гомоморфизмом, если:
наз. гомоморфизмом, если: 
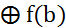
 – если выполняются эти условия
– если выполняются эти условия называется гомоморфизмом, если:
называется гомоморфизмом, если:

 называется изоморфизмом.
называется изоморфизмом.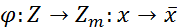 ,
,  - сюрьекция, но не является инъекцией.
- сюрьекция, но не является инъекцией. – это изоморфизм
– это изоморфизм
 гомоморфизм колец,
гомоморфизм колец,  - нуль кольца К’. Прообраз элемента
- нуль кольца К’. Прообраз элемента 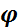 .
.
 является сурьективным гомоморфизмом, его ядро совпадает с I.
является сурьективным гомоморфизмом, его ядро совпадает с I. произв. гомоморфизм, то
произв. гомоморфизм, то 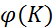 – изоморфно.
– изоморфно.
 имеет единственное решение). Критерий подполя. Мультипликативная группа поля.
имеет единственное решение). Критерий подполя. Мультипликативная группа поля.

 . Z – не поле, т.к обратный элемент ±1 – это не достаточно
. Z – не поле, т.к обратный элемент ±1 – это не достаточно
 Пример2: Поле из 2-х элементов
Пример2: Поле из 2-х элементов 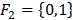 , на каждом «+» и «*» задается таблиц.:
, на каждом «+» и «*» задается таблиц.: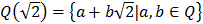
 -кольцо
-кольцо ;
; 
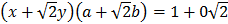

 да
да нет
нет да
да да
да
 да
да нет
нет ,
, 
 , если они изоморфны как кольца.
, если они изоморфны как кольца.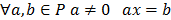 имеет единственное решение:
имеет единственное решение: 
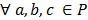






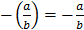
 введём отношение эквивалентности.
введём отношение эквивалентности. 

 =>
=> 
 . Множество всех дробей обозначим Q(K).
. Множество всех дробей обозначим Q(K).

 - нуль
- нуль

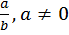


 , (a – фиксированный эл-т из G) мн-во
, (a – фиксированный эл-т из G) мн-во  наз. левым смежным классом группы G по подгруппе H.
наз. левым смежным классом группы G по подгруппе H. – правый смежный класс.
– правый смежный класс. ]. Смежные классы в этом случае состоят из матриц с одинаковыми делителями и детерминантом.
]. Смежные классы в этом случае состоят из матриц с одинаковыми делителями и детерминантом. ) состоят из чисел, которые при делении на m дают одинаковые остатки.
) состоят из чисел, которые при делении на m дают одинаковые остатки. , тогда следующие условия эквивалентны:
, тогда следующие условия эквивалентны:

 является взаимно однозначным соответствием между мн-вом левых смежных классов G по Н и мн-вом правых смежных классов G по Н, т.е. мощность мн-ва левых смежных классов G по Н совпадают с мощностью правых смежных классов G по Н.
является взаимно однозначным соответствием между мн-вом левых смежных классов G по Н и мн-вом правых смежных классов G по Н, т.е. мощность мн-ва левых смежных классов G по Н совпадают с мощностью правых смежных классов G по Н. . [Н ⊲ G]
. [Н ⊲ G] n(ℝ)
n(ℝ) G, тогда:
G, тогда: ,
,  =aH.
=aH. с операцией умножения подмножеств является группой.
с операцией умножения подмножеств является группой. }
} =G/H, тогда отображение f:G -> G/H: a ->
=G/H, тогда отображение f:G -> G/H: a ->  явл. гомоморфизмом. Ядро этого гомоморфизма Ker f = H.
явл. гомоморфизмом. Ядро этого гомоморфизма Ker f = H. .
. не явл. числовым полем, его эл-ты явл. классы эквивалентности по модулю.
не явл. числовым полем, его эл-ты явл. классы эквивалентности по модулю. а
а  Р,
Р,  /n
/n  p имеет место n*a=0.
p имеет место n*a=0. и
и  n*a
n*a  0
0 , тогда n*a=
, тогда n*a= 
 =0⇒n*1=0.
=0⇒n*1=0. то верно рав-но
то верно рав-но  .
.



 .
.

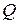 или
или  .
. Р1∩ Р2.
Р1∩ Р2. подполей поля Р,является подполем поля Р.
подполей поля Р,является подполем поля Р. Zp
Zp
 Значит НОД
Значит НОД  u(x),v(x)
u(x),v(x) 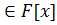
 v(x)p(x)=1
v(x)p(x)=1 v(a)
v(a) 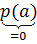 =1
=1
 =
= 
 разделим с остатком на
разделим с остатком на 


 , deg h(x)
, deg h(x)  n-1
n-1 для алгебраического элемента
для алгебраического элемента 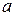 (следствие 1).
(следствие 1). -расширение полей,
-расширение полей,  - алгебраический элемент степени n под F, тогда каждый элемент
- алгебраический элемент степени n под F, тогда каждый элемент  (а) (из простого расширения F(a)), можно представить в виде t=h(a),где h(x) – полином над полем F
(а) (из простого расширения F(a)), можно представить в виде t=h(a),где h(x) – полином над полем F  степень которого deg h(x)
степень которого deg h(x)  такое представление единственное.
такое представление единственное. , где t=h(a), t=
, где t=h(a), t= 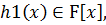
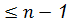



 , то это полином степени
, то это полином степени  над F корнем которого является а.?!
над F корнем которого является а.?! F -расширение полей, а
F -расширение полей, а  Е-алгеброический элемент степени n над F, тогда F(a)=
Е-алгеброический элемент степени n над F, тогда F(a)=  и степень[F(a):F]=n
и степень[F(a):F]=n базис F(a)над F]
базис F(a)над F] F(a) можно записать в виде t=h(a), где h(x)
F(a) можно записать в виде t=h(a), где h(x)  F[x], deg h(x)
F[x], deg h(x)  n-1
n-1



 , f(x)
, f(x)  deg p(x)=n?!
deg p(x)=n?! – конечное расширение поля F.
– конечное расширение поля F. )Ↄ
)Ↄ  ) ↃF.
) ↃF. .
.




