
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные принципы и св-ва эл. цепей.Содержание книги Поиск на нашем сайте
Основ. принципами линейных эл.цепейявл. линейные соотношения м/у элек-ми величинами. В любой эл.цепи состоящей из линейных активных и пассивных эл-ов при изменении 1ой из величин (R,J,U,E) ток в любой ветви m линейно зависит от тока n
Включаем в схему Е’1 и только его 1 рассчитываем по принципу суперпозиции(2):
J1=J3
6.Эквивалентные преобразования пассивных участков электрических цепей. Существует 4 основные вида соединения элементов:1.последовательное соединение.
т.A,B,C-соединены треугольником. Существ.правило, если соединены треугольником, можно соединить звездой: В 1сл. цепь образует треугольник, вершинами которого явл. узлы ABC, а сторонами сопротивления
в обеих схемах токи получаем (3): Для перехода звезды в треугольник используется след.соотношение (4):
Метод контурных токов. Введя понятие о контурных токах можно уменьшить кол-во уров-ий, на их величину равную состав-ых по 1му з-ну Киргофа. Под контурными токами понимаем условные или расчётные токи замыкающиеся в соответс-их контурах. Выберем положительное направление на схеме. Определим сколько на данной схеме независимых контуров(3) и выберем положительное направление обхода каждого контура(обычно для всех контуров одинаково -по часовой стрелке). Для
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.90.57 (0.005 с.) |

 или линейно зависит от напряжения
или линейно зависит от напряжения  . Аналогич. соотношение можно записать и для напряжения на любом элементе какой либо ветви при изменении тока или напряжения в др.ветви. Для решения з-ч использ. принцип суперпозиции, конпенсации и взаимности. Принцип суперпозиции или наложения отражает св-ва независимости действия возбуждающих сил в линейных цепях. В линейных цепях, воздействие нескольких источников эл. энергии на данный эл-нт цепи, можно рассмотр. как результат воздействия на этот элем-т каждого из источ-ов в отдельности. На практике примин-ся след.образом (1):
. Аналогич. соотношение можно записать и для напряжения на любом элементе какой либо ветви при изменении тока или напряжения в др.ветви. Для решения з-ч использ. принцип суперпозиции, конпенсации и взаимности. Принцип суперпозиции или наложения отражает св-ва независимости действия возбуждающих сил в линейных цепях. В линейных цепях, воздействие нескольких источников эл. энергии на данный эл-нт цепи, можно рассмотр. как результат воздействия на этот элем-т каждого из источ-ов в отдельности. На практике примин-ся след.образом (1):
 Принцип суперпозиции.
Принцип суперпозиции. Применение принципа суперпозиции целесообразно, когда состояние цепи определено для каких либо источников ЭДС и токов, и требуется проанализировать электр-ое состояние цепи при изменении напряжений и тока одного из источников. В этом случае нет необходимо вновь рассчитывать значение токов и напряжений от действия всех источников, а достаточно опред-ть лишь частично токи и напряжения от действия дополнительной ЭДС.
Применение принципа суперпозиции целесообразно, когда состояние цепи определено для каких либо источников ЭДС и токов, и требуется проанализировать электр-ое состояние цепи при изменении напряжений и тока одного из источников. В этом случае нет необходимо вновь рассчитывать значение токов и напряжений от действия всех источников, а достаточно опред-ть лишь частично токи и напряжения от действия дополнительной ЭДС.
 . Знак «-» необходимо выбрать. Следует отметить, что метод суперпозиции не применим для расчета мощностей элемента элек-ой цепи, т.к. их значение пропорционально квадрату токов проходящих ч/з них. Принцип компенсации заключается в том, что любой пассивный участок эл-ой цепи, ветвь или её часть с известным напряжением м.б. заменён источником ЭДС с тем же напряжением, а любая ветвь с известным током-источником тока того же значения. Принцип компенсации в ряде случаев облегчает расчёт и анализ электр. цепи. Принцип взаимности применяется для электр. цепей с 1м источником электрич. энергии, и заключается в том, что если ЭДС ветви М в цепи вызывает ток
. Знак «-» необходимо выбрать. Следует отметить, что метод суперпозиции не применим для расчета мощностей элемента элек-ой цепи, т.к. их значение пропорционально квадрату токов проходящих ч/з них. Принцип компенсации заключается в том, что любой пассивный участок эл-ой цепи, ветвь или её часть с известным напряжением м.б. заменён источником ЭДС с тем же напряжением, а любая ветвь с известным током-источником тока того же значения. Принцип компенсации в ряде случаев облегчает расчёт и анализ электр. цепи. Принцип взаимности применяется для электр. цепей с 1м источником электрич. энергии, и заключается в том, что если ЭДС ветви М в цепи вызывает ток  в К-й ветви, то эта же ЭДС действуя в ветви К вызовет ток ветви М, такое же
в К-й ветви, то эта же ЭДС действуя в ветви К вызовет ток ветви М, такое же  .
.
 . 2.параллельное соединение.
. 2.параллельное соединение.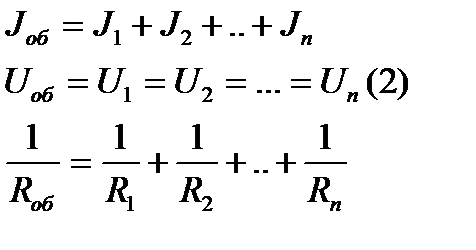
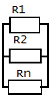 .
. В сложных элект-их цепях встреч.соединения кот. нельзя отнести ни к последовательному, ни к параллельному соединениям. Рассм. для примера цепь.
В сложных элект-их цепях встреч.соединения кот. нельзя отнести ни к последовательному, ни к параллельному соединениям. Рассм. для примера цепь. . Расчет такой цепи удобно производить, используя эквивалентную замену 3 ветвей соединенных треугольником,3мя ветвями соединенными звездой. Определим соотношение эквивалентности м/усопротивлениями обеих схем. Для этого воспольз-ся общим условием эквив-сти, по кот-муU и J в ветвях не подвергнуты преобразованию, должны оставаться без изменения в любых режимах, в том числе при размыкании ветвей, присоед-ых в узлах AB или C.
. Расчет такой цепи удобно производить, используя эквивалентную замену 3 ветвей соединенных треугольником,3мя ветвями соединенными звездой. Определим соотношение эквивалентности м/усопротивлениями обеих схем. Для этого воспольз-ся общим условием эквив-сти, по кот-муU и J в ветвях не подвергнуты преобразованию, должны оставаться без изменения в любых режимах, в том числе при размыкании ветвей, присоед-ых в узлах AB или C.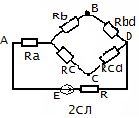 Так при отсоединении резистора Rас от узла С
Так при отсоединении резистора Rас от узла С должны оставаться прежними, и следовательно
должны оставаться прежними, и следовательно  в обеих схемах должно не изменяться, а если это так, то сопротивление участков Rab для 2х схем должно быть = Uab1=Uab2.
в обеих схемах должно не изменяться, а если это так, то сопротивление участков Rab для 2х схем должно быть = Uab1=Uab2. 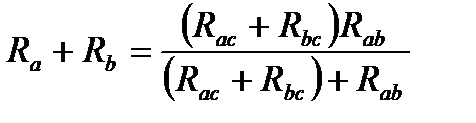 - при условии. что т.С рассоединена с Rcd на 2х схемах. Аналогично, отключаем резисторы от т.АиВ, получаем соотношение(2):
- при условии. что т.С рассоединена с Rcd на 2х схемах. Аналогично, отключаем резисторы от т.АиВ, получаем соотношение(2):  . Решая сис-му относительно
. Решая сис-му относительно 
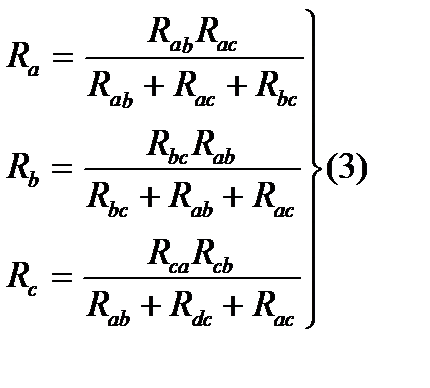 Эквив-оесоот-иепреобр-ниятреуг-ка в звезду.
Эквив-оесоот-иепреобр-ниятреуг-ка в звезду. .
. каждого контура выбираем свой независимый ток, кот-ый совпадает с обходом тока(1).
каждого контура выбираем свой независимый ток, кот-ый совпадает с обходом тока(1). 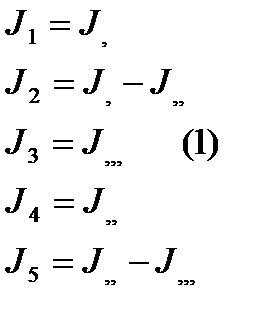 Для определения контурных токов в цепи.составим по 2му з-ну Киргофаур-ние для 3х независимых токов:
Для определения контурных токов в цепи.составим по 2му з-ну Киргофаур-ние для 3х независимых токов:  . Решаем полученную систему Ур-ий относительно неизвестных контурных токов J,/ J,,/J,,,. Определяем их, а затем рассчитываем реальные токи в цепи по полученным ранее формулам.
. Решаем полученную систему Ур-ий относительно неизвестных контурных токов J,/ J,,/J,,,. Определяем их, а затем рассчитываем реальные токи в цепи по полученным ранее формулам.


