
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача на безусловный минимум.Стр 1 из 2Следующая ⇒
Теорема Куна-Таккера. Рассмотрим задачу Опр. Мн-тво планов основной задачи выпуклого программирования регулярно, если существует вектор Усл.(2) наз. условием Слейтера. Геометрич.(2) означает,что у зад.(1) существует такой план Теорема 2. (Куна-Таккера) Для того, чтобы Доказательство. Необходимость. Пусть
1. Доказываем, что множества 2. Докажем, что множества 3. Докажем, что вектор 4. Докажем, что в 5. Докажем, что на Таким образом, пара Ч.т.д Задача на безусловный минимум. Задача имеет вид: Теорема 1. Если Теорема 2 (Необходимое условие оптимальности второго порядка). Если Опр. Точка Теор.3 (Достат. условие оптимальности). Если Замечание. При проверке условий (3) и (5) применяются критерии Сильвестра неотрицательности и положительности квадратных матриц. Схема исследования задач типа (1) 1) Проверяем условие существования решения задачи (1), при этом применяется критерий существования решения 2) Составляем систему (4) и находим стационарные точки функции
3) Для каждой стационарной точки проверяем выполнение или невыполнение условий (3)-(5). Пусть а) б) в)Не выполн. ни а)ни б).Тогда эту точку исключают из дальнейшего рассмотр-я. 4) Делаем вывод: среди точек, оказавшихся либо локально-оптимал. планами, либо подозрительных на решение, находим лучшую, т.е. подставляем точки в целевую ф-цию и лучшей будет точка с наименьшим значением ф-ции. Если док-но существование реш-я и построены все стационарные точки, то лучшая точка будет оптимал. планом. В общем случае, из-за сложности функции
3часть______________________________________________________ Метод равномерного поиска Выбираем некоторое Если Замечание. Можно сразу подобрать
Теорема Куна-Таккера. Рассмотрим задачу
Опр. Мн-тво планов основной задачи выпуклого программирования регулярно, если существует вектор Усл.(2) наз. условием Слейтера. Геометрич.(2) означает,что у зад.(1) существует такой план Теорема 2. (Куна-Таккера) Для того, чтобы Доказательство. Необходимость. Пусть
1. Доказываем, что множества 2. Докажем, что множества 3. Докажем, что вектор 4. Докажем, что в 5. Докажем, что на Таким образом, пара Ч.т.д Задача на безусловный минимум. Задача имеет вид: Теорема 1. Если Теорема 2 (Необходимое условие оптимальности второго порядка). Если Опр. Точка Теор.3 (Достат. условие оптимальности). Если Замечание. При проверке условий (3) и (5) применяются критерии Сильвестра неотрицательности и положительности квадратных матриц.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.24 (0.018 с.) |
 (1), в которой
(1), в которой  – вектор-функция, ф-ции
– вектор-функция, ф-ции 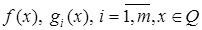 – выпуклые ф-ции;
– выпуклые ф-ции; 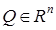 – выпуклое мн-ство простой структуры, т.е. подмн-тво, кот. задается с помощью простейших ограничений на одну переменную (
– выпуклое мн-ство простой структуры, т.е. подмн-тво, кот. задается с помощью простейших ограничений на одну переменную (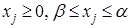 ). Задача наз. основной задачей выпуклого программирования.
). Задача наз. основной задачей выпуклого программирования.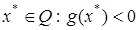 (2)
(2)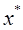 , кот. явл. внутренней точкой по основным ограничениям.
, кот. явл. внутренней точкой по основным ограничениям.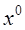 был оптимальный план основной задачи выпуклого программирования, для которой выполняется условие регулярности (2), необходимо и достаточно, чтобы существовал такой вектор
был оптимальный план основной задачи выпуклого программирования, для которой выполняется условие регулярности (2), необходимо и достаточно, чтобы существовал такой вектор  такой, что пара
такой, что пара  является седловой точкой функции Лагранжа и при этом выполн. условие дополняющей не жесткости:
является седловой точкой функции Лагранжа и при этом выполн. условие дополняющей не жесткости:  .
.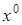 – оптимал. план (1) и выполняется
– оптимал. план (1) и выполняется  . Тогда по нему и параметрам зад.(1) построим три подмножества:
. Тогда по нему и параметрам зад.(1) построим три подмножества: 
 . Ясно, что мн-тво
. Ясно, что мн-тво  явл. границей мн-тва
явл. границей мн-тва  , т.е.
, т.е. 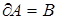

 и
и  выпуклые.
выпуклые. не пересекаются.
не пересекаются. .
. , а так как
, а так как  .
. .
.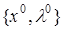 удовлетворяет (3) и, следовательно, является седловой точкой функции Лагранжа.
удовлетворяет (3) и, следовательно, является седловой точкой функции Лагранжа.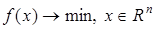 (1), то есть
(1), то есть  .
. (2)
(2) (3)
(3)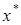 наз. стационарной точкой функции
наз. стационарной точкой функции 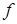 , если она является решением системы
, если она является решением системы 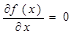 (4)
(4)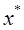 – стационарная точка ф-ции
– стационарная точка ф-ции 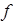 и
и  , (5) то
, (5) то 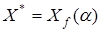 . В общем случае, при
. В общем случае, при 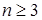 , вызывает трудности проверка условий существования решения, так как в редких случаях можно представить (построить) множество уровня.
, вызывает трудности проверка условий существования решения, так как в редких случаях можно представить (построить) множество уровня.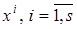 – все стационарные точки функции
– все стационарные точки функции 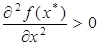 . Тогда, согласно теореме 3
. Тогда, согласно теореме 3 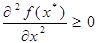 . Тогда для нее выполн. условия теор.2, но не выполн. условия теор.3. Тем не менее, она остается подозрительной на решение зад.(1) (т.е. она может оказаться и оптимальным планом и локально-оптимальным планом).
. Тогда для нее выполн. условия теор.2, но не выполн. условия теор.3. Тем не менее, она остается подозрительной на решение зад.(1) (т.е. она может оказаться и оптимальным планом и локально-оптимальным планом).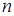 и разбиваем исходный отрезок [
и разбиваем исходный отрезок [ 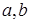 ] на
] на 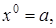
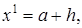
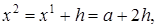 …,
…, 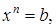 где
где 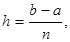 и поочерёдно начиная с
и поочерёдно начиная с 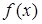 . В силу унимодальности будут выполняться неравенства
. В силу унимодальности будут выполняться неравенства  . Тогда ясно, что
. Тогда ясно, что 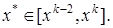
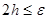 , то задача локализации решена. В противном случае выбираем
, то задача локализации решена. В противном случае выбираем 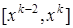 и разбиваем его на некоторое количество частей и операцию поиска повторяем. В конце концов, задача (1) будет решена.
и разбиваем его на некоторое количество частей и операцию поиска повторяем. В конце концов, задача (1) будет решена. таким образом, чтобы выполнялось
таким образом, чтобы выполнялось 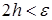 , но это не рационально, так как количество точек перебора будет очень большим. Лучше на 1-ом этапе исходный отрезок разбить на количество частей
, но это не рационально, так как количество точек перебора будет очень большим. Лучше на 1-ом этапе исходный отрезок разбить на количество частей 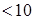 , потом количество точек увеличить.
, потом количество точек увеличить.


