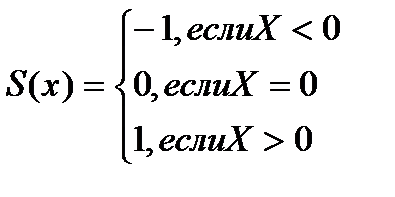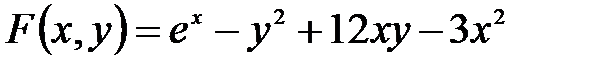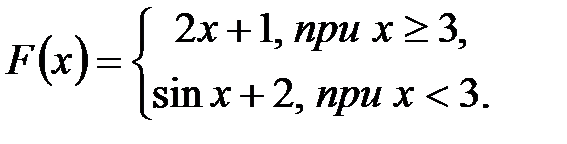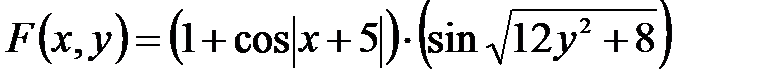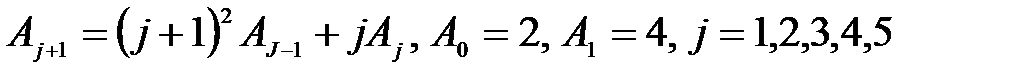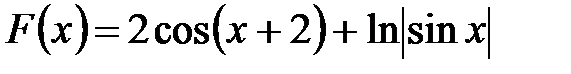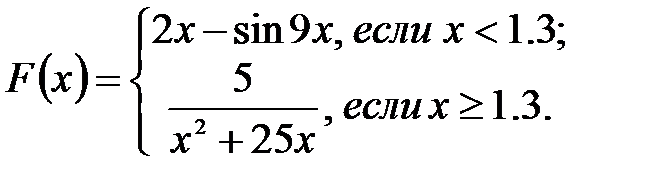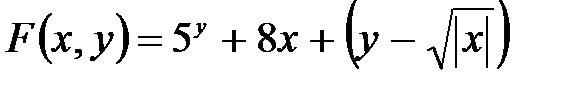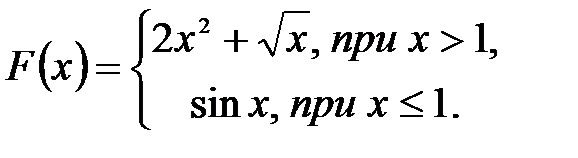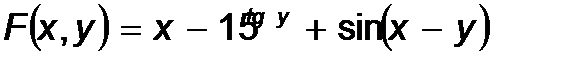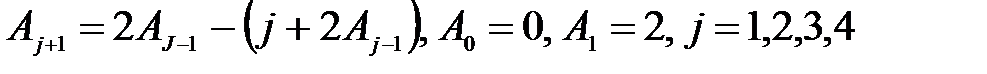Правила выполнения практических/лабораторных работ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для проведения практических/лабораторных работ

 

по дисциплине Информатика и ИКТ (1 курс)

 

для студентов специальности

151901 Технология машиностроения

230115 Программирование в компьютерных системах

190631 Техническое обслуживание и ремонт автомобильного транспорта

140448 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)

080114 Экономика и бухгалтерский учет (по отраслям)

 

 

2012

Методические указания для проведения практических/лабораторных работ

по дисциплине Информатика и информационно-коммуникационные технологии (далее – ИКТ) (1 курс) для студентов специальности:

151901 Технология машиностроения;

230115 Программирование в компьютерных системах;

190631 Техническое обслуживание и ремонт автомобильного транспорта;

140448 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям);

080114 Экономика и бухгалтерский учет (по отраслям)

 

 

Составитель: Тимофеева Е.В., преподаватель специальных дисциплин

Майер Ю.В., преподаватель специальных дисциплин

Палкина Г.И., преподаватель специальных дисциплин

Рекомендовано к использованию решением методического советаГБОУ СПО (ССУЗ) «Златоустовский индустриальный колледж им.П.П. Аносова» (протокол № ____ от ____ ________ 20____г.)

СОДЕРЖАНИЕ

 

ПРЕДИСЛОВИЕ. 5

ПРАВИЛА ВЫПОЛНЕНИЯ ПРАКТИЧЕСКИХ/ЛАБОРАТОРНЫХ РАБОТ. 6

ПРАКТИЧЕСКАЯ РАБОТА №1 Системы счисления. 7

ПРАКТИЧЕСКАЯ РАБОТА №2 Основы алгоритмизации. 17

ЛАБОРАТОРНАЯ РАБОТА №3 Операционная система Windows. 29

ЛАБОРАТОРНАЯ РАБОТА №4 Файловый менеджер FreeCommander 37

ЛАБОРАТОРНАЯ РАБОТА №5 MICROSOFT OFFICE WORD 2007. Создание, форматирование текстового документа. 43

ЛАБОРАТОРНАЯ РАБОТА №6 MICROSOFT OFFICE WORD 2007. Работа с таблицами 51

ЛАБОРАТОРНАЯ РАБОТА №7 MICROSOFT OFFICE WORD 2007. Работа с графическими объектами. 59

ЛАБОРАТОРНАЯ РАБОТА №8 MICROSOFT OFFICE WORD 2007. Создание комплексных текстовых документов. 66

ЛАБОРАТОРНАЯ РАБОТА №9 MICROSOFT OFFICE EXCEL 2007. Создание, форматирование электронных таблиц. 70

ЛАБОРАТОРНАЯ РАБОТА №10 MICROSOFT OFFICE EXCEL 2007. Работа с мастером функций. 79

ЛАБОРАТОРНАЯ РАБОТА №11 MICROSOFT OFFICE EXCEL 2007. Статистическая обработка данных. 87

ЛАБОРАТОРНАЯ РАБОТА №12 MICROSOFT OFFICE EXCEL 2007. Расчет заработной платы и расходов на командировку. 93

ЛАБОРАТОРНАЯ РАБОТА №13 MICROSOFT OFFICE ACCESS 2007. Создание и связывание таблиц. 99

ЛАБОРАТОРНАЯ РАБОТА №14 MICROSOFT OFFICE ACCESS 2007. Создание запросов. 109

ЛАБОРАТОРНАЯ РАБОТА №15 MICROSOFT OFFICE ACCESS 2007. Создание форм 118

ЛАБОРАТОРНАЯ РАБОТА №16 MICROSOFT OFFICE ACCESS 2007. Создание отчетов. 128

ЛАБОРАТОРНАЯ РАБОТА №17 MICROSOFT OFFICE POWERPOINT 2007. Создание слайда с текстом. 138

ЛАБОРАТОРНАЯ РАБОТА №18 MICROSOFT OFFICE POWERPOINT 2007. Работа с рисунками, анимацией, видео. 144

ЛАБОРАТОРНАЯ РАБОТА №19 MICROSOFT OFFICE POWERPOINT 2007. Работа с гиперссылкой, таблицами, диаграммами. 155

ЛАБОРАТОРНАЯ РАБОТА №20 INTERNET. Знакомство с Википедией. 164

 

 

ПРЕДИСЛОВИЕ

Методические указания составлены для студентов среднего специального учебного заведения в соответствии с требованиями Федерального государственного образовательного стандарта. Сборник должен оказать действенную помощь в усвоении важнейших понятий, определений и способствовать эффективному использованию учебного времени при овладении дисциплины Информатика и информационно-коммуникационные технологии (далее – ИКТ) (1 курс).

Цель данной методической разработки - помочь студентам овладеть базовыми знаниями, необходимыми для работы пользователю на персональном компьютере.

Методические указания способствуют овладению:

− основными понятиями систем счисления, основ алгоритмизации;

− способами эффективной работы в операционной системе Windows, глобальной сети Internet;

− навыками практической деятельности при создании текстовых документов в Microsoft Office Word 2007, электронных таблиц в Microsoft Office Excel 2007, баз данных в Microsoft Office Access 2007, презентаций в Microsoft Office PowerPoint 2007.

Приводятся методические указания к проведению практических/лабораторных работ и соответствующие практические/лабораторные задания. Работы выполняются в рамках дисциплины Информатика и ИКТ и ориентированы на изучение основных дидактических единиц. Материал методических указаний может быть использован как для самостоятельного изучения, так и для обучения в группах.

ПРАВИЛА ВЫПОЛНЕНИЯ ПРАКТИЧЕСКИХ/ЛАБОРАТОРНЫХ РАБОТ

Практические/лабораторные работы выполняются каждым студентом самостоятельно в полном объеме и согласно содержанию методических указаний.

Перед выполнением работы студент должен отчитаться перед преподавателем за выполнение предыдущей работы (сдать отчет).

Студент должен на уровне понимания и воспроизведения предварительно усвоить необходимую для выполнения лабораторных работ теоретическую и практическую информацию.

Студент, получивший положительную оценку и сдавший отчет по предыдущей работе, допускается к выполнению следующей.

Студент, пропустивший практическую/лабораторную работу по уважительной либо неуважительной причине, закрывает задолженность в процессе выполнения последующих работ.

ПРАКТИЧЕСКАЯ РАБОТА №1

Системы счисления

Цели работы:

- изучить понятие системы счисления;

- изучить алгоритмы перевода чисел из одной позиционной системы счисления в другую;

- получить представление об арифметических действиях с числами в любой позиционной системе счисления.

В результате выполнения практической работы студент должен:

знать:

- понятие системы счисления;

- понятие позиционной системы счисления;

- понятие непозиционной системы счисления;

уметь:

- переводить числа из одной системы счисления в другую;

- выполнять основные арифметические операции в любой системе счисления при помощи стандартного приложения Windows Калькулятор.

Пояснения к работе

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления.

Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.

Все системы счисления делятся на две большие группы:

− позиционные

− непозиционные.

Система называется непозиционной, если значение каждой цифры (ее вес) НЕ изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Используется 7 знаков: I – 1, V – 5, X – 10, L – 50, C – 100, D – 500, M – 1000.

Например, римское число XXI, в котором X=10, I=1 (10+10+1=21).

Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.

Например, арабское число 424 означает, что левая «4» - это четыре сотни (400), «2» - это два десятка, а правая «4» - это четыре единицы.

Для записи чисел в различных системах счисления используется некоторое количество отличных друг от друга знаков. Число таких знаков в позиционной системе счисления называется основанием системы счисления. Если количество таких цифр равно P, то система счисления называется P -ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.

В настоящее время люди для счета в основном используют десятичную систему счисления, в которой десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Для представления информации в компьютерах используется двоичная позиционная система счисления, так как компьютеры могут распознавать и сохранять не более двух различных состояний (цифр):

− устройство подключено – не подключено;

− участок поверхности лазерного диска отражает – не отражает и т.д.

В двоичной системе счисления используют две цифры - 0 и 1.

Запись произвольного числа x в P -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена

x = a_nPⁿ + a_{n -1} P^{n -1} +... + a ₁ P ¹ + a ₀ P ⁰ + a _-1 P ^-1 +... + a_-nP^-n

Примеры: (индексы внизу указывает основание системы счисления)

23,43(₁₀) = 2*10¹ + 3*10° + 4*10^-1 + 3*10^-2

(в данном примере «3» в одном случае означает число единиц, а в другом - число сотых долей единицы);

692(₁₀) = 6* 10² + 9*10¹ + 2

(«Шестьсот девяносто два» с формальной точки зрения представляется в виде «шесть умножить на десять в степени два, плюс девять умножить на десять в степени один, плюс два»).

1101(₂)= 1*2³ + 1*2²+0*2¹+ 1*2°

При переводе чисел из десятичной системы счисления в систему с основанием P>1 обычно используют следующий алгоритм:

1. если переводится целая часть числа, то она делится на P, после чего запоминается остаток от деления. Полученное частное вновь делится на P, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на P выписываются в порядке, обратном их получению;

2. если переводится дробная часть числа, то она умножается на P, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на P и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю. Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием P.

Конкретизируем описанный выше способ в случае перевода чисел из десятичной системы в двоичную (см. табл. 1.1, 1.2). Целая и дробная части переводятся порознь.

 

Таблица 1.1. Перевод целого числа

из десятичной системы в двоичную

Десятичное число / целое частное	Делитель (основание системы)	Остаток
25(10)=11001(2).

 

 

Таблица 1.2. Перевод дробной части числа

из десятичной системы в двоичную

Десятичная дробь / дробная часть произведения	Множитель (основание системы)	Целая часть произведения
0,25
0,50
0,00
0,25(10)=0,01(2).

 

	*2
	*2

 

Для перевода числа из любой системы счисления в десятичную необходимо:

1. пронумеровать цифры целой части справа налево цифрами 0, 1, 2…

2. пронумеровать цифры дробной части слева направо цифрами -1, -2, -3…

3. найти сумму произведений цифр на основание системы счисления в степени, равной порядку этой цифры в данном числе.

435,67 = 4*10² + 3*10¹ + 5*10° + 6*10^-1 + 7*10^-2

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию P системы счисления.

Для выполнения переводов из одной системы счисления в другую или арифметических операций, используется стандартная программа Windows Калькулятор. Для ее запуска необходимо:

1. выполнить команду меню Пуск ® Все программы ® Стандартные ® Калькулятор;

2. затем в меню Вид выбрать Инженерный;

3. для выбора системы счисления используется переключатель с соответствующими значениями (HEX – шестнадцатеричная система счисления, DEC - десятичная система счисления, OCT – восьмеричная система счисления, BIN – двоичная система счисления).

Задание

1. При домашней подготовке студент должен повторить принципы перевода чисел из одной позиционной системы счисления в другую и правила выполнения арифметических операций.

2. Предоставить отчет.

Варианты заданий

Вариант 1

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

110100112

1D,EC816

123,418

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

1011,0012 =?10

35616 =?10

0328 =?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

13410 =?2

13410 =?8

13410 =?16

5. Вычислите значения выражения, используя Калькулятор:

1010₁₀ - 12₈=?₁₆

Вариант 2

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

10213

788

1А16

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

1001,1012 =?10

A1F416 =?10

23,434 =?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

69210 =?8

832,1510 =?2

4586110 =?2

5. Вычислите значения выражения, используя Калькулятор:

1,010₂ + 231₈ + 10A₁₆ =?₂

Вариант 3

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

11012

1779

FF16

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

1010,1112 =?10

110116=?10

1128=?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

341,510 =?2

13410 =?8

457,110 =?2

5. Вычислите значения выражения, используя Калькулятор:

106₁₆ – 1101,1101₂=?₁₀

Вариант 4

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

101111015

1678

9AF216

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

1128 =?10

11012 =?10

341,58 =?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

123,110 =?2

69210=?16

13410 =?8

5. Вычислите значения выражения, используя Калькулятор:

A,B₁₆ + E,F₁₆=?₂

Вариант 5

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

10101012

77518

CDEF16

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

111,0012 =?10

101,1018 =?10

D8,AC16 =?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

23,4310 =?2

435,6710 =?8

13410 =?16

5. Вычислите значения выражения, используя Калькулятор:

625₈ * 712₈=?₂

Вариант 6

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

10002

20,018

AA0C16

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

10110,12 =?10

5D8,A116 =?10

1414,18 =?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

8721,110 =?2

789,11110 =?8

65410 =?16

5. Вычислите значения выражения, используя Калькулятор:

1011,11₂ + 111,1₂=?₈

Вариант 7

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

11102

10,0008

100016

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

0,AAF7316 =?10

0,7518 =?10

0,10112 =?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

8654,510 =?2

0,12110 =?8

43110 =?16

5. Вычислите значения выражения, используя Калькулятор:

101₂ * 1111001₂=?₁₀

Вариант 8

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

10101,12

348

CE816

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

CD,35616 =?10

3F5A616 =?10

356,AA16 =?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

49210 =?2

134,7510 =?8

0,78210 =?16

5. Вычислите значения выражения, используя Калькулятор:

A,B₁₆ * E,F₁₆=?₁₆

Вариант 9

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

001010,012

148

28,116

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

72,2438 =?10

3318 =?10

18D916 =?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

842110 =?2

0,44410 =?8

1,3410 =?16

5. Вычислите значения выражения, используя Калькулятор:

7,5₁₀ + 14,6₈=?₁₆

Вариант 10

1. Запишите дату своего рождения (число, месяц, год) в римской системе счисления.

2. Запишите следующие числа в виде многочлена:

1011012

10003

3000D16

3. Перевести числа в десятичную систему счисления не используя Калькулятор:

0,61648 =?10

AD3,4616 =?10

0,C7416 =?10

4. Перевести числа из десятичной системы счисления не используя Калькулятор:

75110 =?2

0,13410 =?8

130410 =?16

5. Вычислите значения выражения, используя Калькулятор:

1101,001₂ / 10,1₂ =?₈

Работа в лаборатории

1. Выполнить предложенные задания согласно варианту.

2. Сформировать отчет.

Содержание отчета

1. Исходные данные.

2. Результаты вычислений.

Контрольные вопросы

1. Что такое система счисления?

2. Что такое позиционная система счисления? Приведите пример.

3. Что такое непозиционная система счисления? Приведите пример.

4. Особенности двоичной системы счисления.

5. Особенности восьмеричной системы счисления.

6. Особенности шестнадцатеричной системы счисления.

7. Как производится перевод чисел из одной системы счисления в другую?

ПРАКТИЧЕСКАЯ РАБОТА №2

Основы алгоритмизации

Цели работы:

− изучение этапов разработки программы;

− изучение различных способов описания алгоритмов.

В результате выполнения практической работы студент должен:

знать:

− понятие алгоритма;

− требования к алгоритму;

− способы описания алгоритмов;

− основные алгоритмические конструкции;

уметь:

− составлять блок-схемы алгоритмов;

− описывать простые алгоритмы любым способом.

Пояснения к работе

Само слово «алгоритм» происходит от algorithmi - латинской формы написания имени великого математика IX века аль-Хорезми, который сформулировал правила выполнения арифметических действий. Первоначально под алгоритмами и понимали только правила выполнения четырех арифметических действий над многозначными числами.

Алгоритм – система формальных правил (команд), однозначно определяющих процесс решения задач.

Алгоритм – конечная последовательность общепонятных предложений, формальное, не требующее проявления человеческой изобретательности, исполнение которых позволяет за конечное время получить решение некоторой задачи из некоторого класса задачи.

Алгоритм должен удовлетворять определенным требованиям:

1. Наличие ввода исходных данных.

2. Определенность (детерминированность) – свойство, заключающееся в том, что каждое действие, правило алгоритма должно быть точно (однозначно) определено. Для однозначно понимаемой формы записи действий используют языки программирования.

3. Конечность – свойство, заключающееся в том, что работа алгоритма должна заканчиваться после выполнения конечного числа действий (шагов, операций). Типичными действиями алгоритма являются ввод данных, обработка данных, вывод результатов в определенной форме.

4. Массовость – свойство, заключающееся в возможности решения задачи с различными вариантами наборов данных. Наличие этого свойства имеет важное практическое значение, так как обеспечивает возможность получения результатов, используя однажды разработанный алгоритм.

5. Эффективность – для задачи должны использоваться ограниченные ресурсы компьютера (процессорное время процессора, объем оперативной памяти и так далее).

6. Наличие вывода результата выполнения.

Для представления алгоритмов могут использоваться различные формы:

− словесное описание;

− словесно-формульное описание;

− блок-схема (схема программы, схема данных и др.);

− запись на языке программирования и другие.

Словесное описание – представление алгоритма с помощью литературного или профессионального языка. Такое описание используется для изложения общей идеи, метода решения задачи. Это может быть инструкция по обработке документов, технология подготовки отчетов и т.п. документы, в которых излагается последовательность действий, понятных исполнителю.

Например, расчет бухгалтером почасовой заработной платы может быть описан следующим образом:

− получить табели учета рабочего времени сотрудников из подразделения;

− проверить правильность данных (количество часов, отработанных каждым сотрудником не должно превышать количества часов в текущем месяце и др.);

− умножить тарифную ставку сотрудника на количество отработанных часов;

− добавить начисления на зарплату (надбавки за руководство, премиальные и т.д.);

− вычесть удержания из заработной платы (подоходный налог, выплаты на погашение ссуды и др.);

− вычислить суммы по подразделениям, по предприятию;

− оформить ведомости на выдачу заработной платы.

Словесно-формульное описание – описание, в котором используются математические формулы.

Пример: решение квадратного уравнения

− ввести численные значения исходных данных - а, b, c;

− вычисление дискриминанта по формуле - ;

− если , то существует только одно решение ;

− если , то решений не существует;

− если , то существует два решения ;

− вывести результат вычислений.

Блок-схема алгоритма – представление алгоритма в графической форме, в которой действия над данными изображаются в виде геометрических блоков с поясняющими надписями, а последовательность действий указывается соединительными линиями. Эта форма используется для наглядного представления процессов обработки данных, особенно в случаях с большим количеством проверок логических условий и разветвлений процессов (выбора последующих действий в зависимости от результатов предыдущих).

Основные графические символы блок-схем представлены в таблице 2.1:

Таблица 2.1 - Графические символы

 

Символ	Наименование символа	Описание
	Данные	Символ отображает данные, носитель данных не определен

 

Продолжение таблицы 2.1

	Процесс	Символ отображает функцию обработки данных любого вида
	Условие	Символ отображает решение или функцию переключательного типа, имеющую один вход и ряд альтернативных выходов, один и только один из которых может быть активизирован после вычисления условий, определенных внутри этого символа.
	Граница цикла	Символ, состоящий из двух частей, отображает начало и конец, цикла.
	Линия	Символ отображает поток данных или управления
	Терминатор	Символ отображает выход во внешнюю среду и вход из внешней среды (начало или конец схемы программы, внешнее использование и источник или пункт назначения данных)

 

В теории алгоритмов доказывается, что любой алгоритм может быть представлен в виде комбинации трех алгоритмических структур:

1. Следование. Представляет собой последовательное выполнение действий (рис. 2.1).

Рис. 2.1 – Следование

Пример: составить блок-схему вычисления суммы двух чисел А и В

Начало

Ввод А, В

Х:=А+В

Вывод Х

Конец

Рис. 2.2 – Блок-схема следования

2. Ветвление. Применяется в случае, когда в зависимости от истинности некоторого логического условия необходимо выполнить то или иное действие (рис. 2.3).

Рис. 2.3 - Ветвление

Можно записать: ЕСЛИ условие ТО действие 1 ИНАЧЕ действие 2.

Действия 1 и 2 могут, в свою очередь, включать в себя другие алгоритмические структуры.

Пример: составить блок-схему ветвления. Если условие А ≥ В истинно, то выполняется операция X= А * В, в противном случае выполняется X = А + В.

 

Начало

Ввод А, В

Х:=А+В

Вывод Х

Конец

A>B

Х:=А*В

 

Рис. 2.4 – Блок-схема ветвления

3. Цикл. Применяется, когда некоторые действия необходимо выполнить несколько раз. Существуют две разновидности цикла.

3.1. Цикл До. Применяется, когда некоторые операции надо повторять до тех пор, пока некоторое условие не станет ложным (рис. 2.5).

Рис. 2.5 - Цикл До

Под начальными присвоениями подразумеваются операции присваивания исходных значений переменным, используемым в цикле. Многократно повторяемая последовательность действий называется телом цикла.

3.2. Цикл Пока. Применяется, когда некоторые операции надо повторять до тех пор, пока некоторое условие не станет истинным (рис. 2.6).

Рис. 2.6 - Цикл Пока

Пример: составить блок-схему алгоритма вычисления факториала (рис. 2.7). Переменной N!, которая в результате выполнения алгоритма должна получить значение факториала, присваивается первоначальное значение 1. Переменной К также присваивается значение 1. Цикл будет выполняться, пока справедливо условие N ≥ К. Тело Цикла состоит из двух операций N!=N!*K и K=K+1.

Начало

Ввод N

K:=1; N!:=1

K<N

N!:= N! * K K:= K + 1

Вывод N!

Конец

 

 

Рис. 2.7 – Блок-схема цикла Пока

Пример: составить блок-схему алгоритма вычисления функции

Запишем этот алгоритм словами:   Ввод Х ЕСЛИ Х< 0 ТО S=-1 ИНАЧЕ ЕСЛИ X=0 ТО S=0 ИНАЧЕ S = 1 Конец ветвления Вывод S Конец.

Программа на алгоритмическом языке – запись алгоритма с использованием операторов выбранного языка программирования. Текст программы, написанной на языке высокого уровня, понятен человеку (программисту). После преобразования этого текста в программу, состоящую из команд ЭВМ, можно выполнить решение задачи по разработанному алгоритму на ЭВМ. Для составления программ на каком-либо языке программирования следует изучить этот язык (алфавит, операторы), приемы использования для решения типовых задач.

Задание

1. При домашней подготовке составить алгоритмы согласно предложенным вариантам (см. варианты заданий).

2. Предоставить отчет.

Варианты заданий

Вариант 1

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Вариант 2

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Вариант 3

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Вариант 4

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Вариант 5

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Вариант 6

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Вариант 7

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Вариант 8

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Вариант 9

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Вариант 10

1. Словесным описанием составить алгоритм перехода дороги по сигналу светофора.

2. Составить блок-схему

3. Словесно-формульным описанием записать алгоритм вычисления функции

4. Составить блок-схему

Работа в лаборатории

1. Выполнить предложенные задания согласно варианту.

2. Создать отчет.

Содержание отчета

1. Выполненные блок-схемы.

Контрольные вопросы

1. Что такое алгоритм?

2. Какие требования предъявляются к алгоритмам?

3. В каких формах может быть представлен алгоритм? Примеры.

4. Какие графические символы используются в схемах программ?

5. Какие виды алгоритмов существуют?

ЛАБОРАТОРНАЯ РАБОТА №3

ЛАБОРАТОРНАЯ РАБОТА №4

ЛАБОРАТОРНАЯ РАБОТА №5

ЛАБОРАТОРНАЯ РАБОТА №6

MICROSOFT OFFICE WORD 2007. Работа с таблицами

Цель работы:

- научиться создавать таблицы;

- научиться производить вычисления в таблицах;

- научиться работать со встроенными функциями;

- научиться добавлять формулы с помощью Редактора формул.

В результате выполнения лабораторной работы студент должен:

знать:

- функциональные возможности Word;

уметь:

- создавать таблицы;

- вводить информацию;

- форматировать информацию;

- производить расчеты по формулам;

- работать со встроенными функциями;

- добавлять формулы с помощью Редактора формул.

Пояснения к работе