Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема про зміну кількості рухуСодержание книги Поиск на нашем сайте
Загальні теореми динаміки
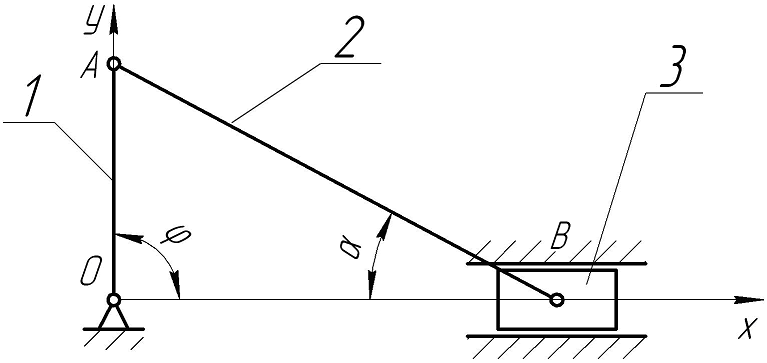
2.2 Теорема про рух центра мас 2.2.1 Визначити абсцису Хс центра мас кривошипно-повзунного механізму при кутах j =900 і a = 300, якщо маса кривошипа 1 дорівнює 4 кг, а маса шатуна 2 дорівнює 8 кг. Шатун 2 довжиною 0,8 м вважати однорідним стрижнем. Масою повзуна 3 нехтуємо.
2.2.2 Визначити координату Yс центра мас кривошипно-повзунного механізму при кутах j =900 і a = 300, якщо маса кривошипа 1 дорівнює 4 кг, а маса шатуна 2 дорівнює 8 кг. Шатун 2 довжиною 0,8 м та кривошип 1 вважати однорідними стрижнями. Масою повзуна 3 нехтуємо.
2.2.3 Визначити абсцису Хс центра мас кривошипно-повзунного механізму при кутах j =900 і a = 300, якщо маса кривошипа 1 дорівнює 6 кг, а маса шатуна 2 дорівнює 10 кг. Шатун 2 довжиною 1 м та кривошип 1 вважати однорідними стрижнями. Маса повзуна зосереджена в т. В і дорівнює 2кг.
Теорема про зміну кількості руху Імпульс сили. Кількість руху 2.3.1.1. Постійна за напрямом сила діє на тіло на протязі 10 с. Визначити модуль її імпульсу за цей час, якщо проекції сили на осі координат Fx=3H; Fy=4H.
2.3.1.4. На матеріальну точку М діє сила
2.3.1.5. На матеріальну точку М діє сила
2.3.1.6. На матеріальну точку М діє сила
2.3.1.7. Матеріальна точка масою m=1 кг рухається по прямій з постійним пришвидшенням а=5 м/с2. Визначити імпульс рівнодійної прикладених до точки сил за проміжок часу τ = t2-t1 , де t2 =4с. t1 =2c.
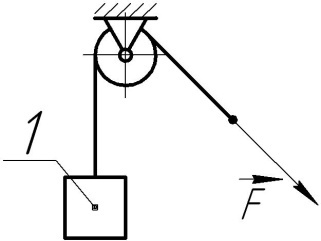
2.3.1.9. Шків 1 радіусом R=0,4 м, що обертається з кутовою швидкістю ω=2,5 рад/с, піднімає вантаж 2 масою m=10 кг. Визначити модуль кількості руху вантажу.
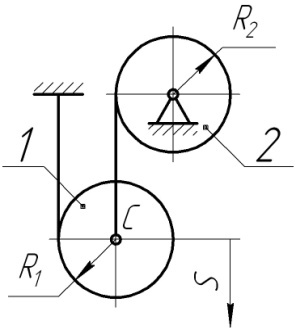
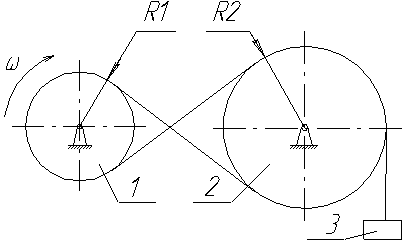
2.3.1.10. Шків 1 радіусом R1=0,2м, що обертається з кутовою швидкістю ω=2,4 рад/с, через колесо 2 радіусом R2=0,4м піднімає вантаж 3 масою m=10 кг. Визначити модуль кількості руху вантажу.
Теорема про зміну кількості руху 2.3.2.1 Матеріальна точка масою 0,5кг рухається по прямій. Визначити модуль імпульсу рівнодійної всіх сил, що діють на точку за перші 2с, якщо вона рухається за законом в) 24 Н·с
2.3.2.13 Поїзд рухається по прямій горизонтальній ділянці шляху зі швидкістю V=20м/с. При гальмуванні розвивається сила опору, рівна 0,2 вазі поїзда. Через який час поїзд зупиниться? г)» 10,19 с
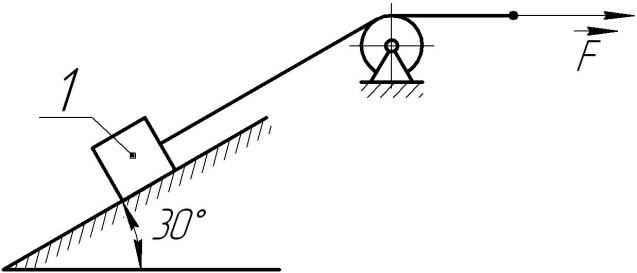
2.3.2.14 Тілу, що ковзає по гладким похилим напрямним, надана початкова швидкість
2.3.2.15 Тіло, якому надали початкову швидкість
2.3.2.16 Тіло, якому надали початкову швидкість
2.3.2.17 Тіло, якому надали початкову швидкість
2.3.2.19 По горизонтальній ділянці шляху рухаються два вагони з масами відповідно
Теорема про зміну кінетичного моменту Момент кількості руху 2.4.24 Однорідний диск 1 радіусом r = 0.5 м та масою m
2.4.25 Циліндр 1 обертається з кутовою швидкістю
2.4.26 На барабан 2, момент інерції якого відносно осі обертання
Теорема про зміну кінетичної енергії Робота і потужність сили 2.5.1.1 Пружину, коефіцієнт жорсткості якої С=100Н/м, розтягнули на 0,02м. Визначити роботу сили пружності пружини.
Кінетична і потенціальна енергіЇ Матеріальної точки 2.5.2.1 Матеріальна точка масою m=1кг рухається по колу зі швидкістю V=1м/с. Яка кінетична енергія цієї точки?
2.5.2.2 Точка масою m=4кг рухається прямолінійно згідно з рівнянням S=4t+2t²(м). Визначити кінетичну енергію точки в момент часу t=2с.
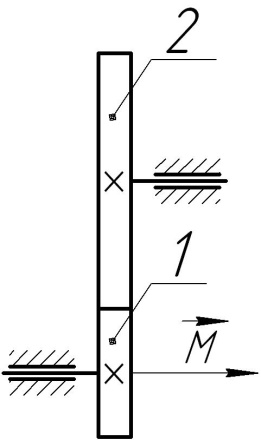
2.5.2.8 Трубка 1 рівномірно обертається з кутовою швидкістю ω=2 рад/с навколо осі АВ. В середині трубки рухається кулька 2 з відносною швидкістю Vr =0,2 м/с та масою m2 =0,5 кг. Визначити кінетичну енергію кульки в момент, коли вона знаходиться на відстані l =0,5м від осі.
Хокеїст, що знаходиться на відстані 10м від воріт, ключкою надає шайбі, яка знаходиться на льоду, швидкість 8м/с. Шайба, ковзаючи по льоді, влітає у ворота зі швидкістю 7,7м/с. Визначити коефіцієнт тертя ковзання між шайбою і поверхнею льоду.
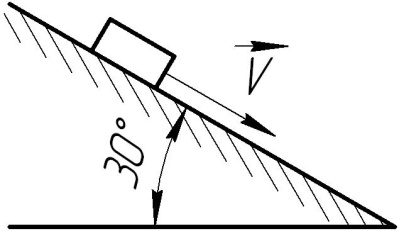
2.5.5.13 По похилій площині опускається без початкової швидкості тіло масою
2.5.5.14 По похилій площині опускається без початкової швидкості вантаж. Яку швидкість
Однорідний диск радіусом 0,4м може обертатися навколо горизонтальної осі, що перпендикулярна до площини диска і проходить через точку, яка знаходиться на його ободі. Яку початкову кутову швидкість необхідно надати диску, щоб він повернувся на чверть оберту?
2.5.6.2 Яку початкову кутову швидкість
2.5.6.3 Тілу, що має вертикальну нерухому вісь обертання надана кутова швидкість
2.5.6.4 Ротору масою
2.5.6.5 До вала АВ жорстко прикріплений горизонтальний однорідний стрижень довжиною
2.5.6.6 Математичний маятник 1 масою
2.5.6.8 Однорідний диск масою т радіусом
2.5.6.10 Стовбур зрізаного дерева радіусом
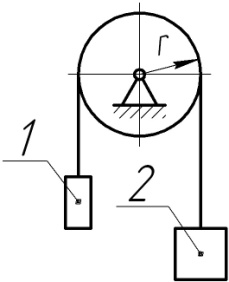
Механічної системи 2.5.7.1 Через нерухомий блок перекинута нитка до кінців якої підвішені вантажі масою
2.5.7.2 Вантажі 1 і 2 масою
2.5.7.3 Вантажі 1 і 2 однакової маси
2.5.7.4 Однакові зубчасті колеса 1 і 2 масою 2кг кожний приводяться в рух зі стану спокою постійною парою сил з моментом
2.5.7.5 Пасова передача починає рух зі стану спокою під дією постійного моменту пари сил
2.5.7.6 Момент інерції зубчастого колеса 1 відносно горизонтальної осі обертання дорівнює 0,1кг×м2, а радіус колеса
2.5.7.7 Однорідні циліндричні котки 1 і 2 масою 20кг і радіусом
2.5.7.8 Зі стану спокою пасова передача починає рух під дією постійного моменту
2.5.7.9 Блоки 1 і 2 з однаковими масами та радіусами, тобто
2.5.7.10 Блоки 1 і 2 з однаковими масами та радіусами, тобто
Динаміка твердого тіла ПРИНЦИП ДАЛАМБЕРА Загальне рівняння динаміки 6.1 Застосування загального рівняння динаміки для опису руху системи сил 6.1.1 Вантажі 1 і 2, маси яких m2 = 2m1, прикріплені до троса, що перекинутий через блок радіусом r. Нехтуючи масою блока, визначити пришвидшення вантажів.
6.1.2 Вантажі 1 і 2, маси яких m2=2m1, прикріплені до троса, що перекинутий через блок радіусом r. Визначити пришвидшення вантажів, враховуючи, що маса блока m3 = m2 рівномірно розподілена по об’єму.
6.1.3 Два вантажа, маси яких m1 = m3 = 2 кг, з’єднані між собою ниткою, перекинутою через блок 2, масою якого можна знехтувати. Визначити пришвидшення вантажів, якщо коефіцієнт тертя ковзання між вантажем 1 і площиною f =0,1.
6.1.4 Два вантажі, маси яких m3 = 2m1 = 6 кг, з’єднані між собою ниткою, перекинутою через блок 2, маса якого m2 = 4кг рівномірно розподілена по ободу радіусом r. Визначити пришвидшення вантажів, якщо коефіцієнт тертя ковзання між вантажем 1 і площиною f =0,12.
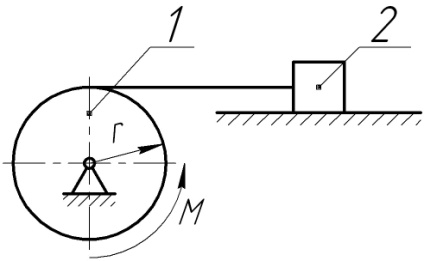
6.1.7 На барабан 1 радіусом r = 0,1 м намотана нитка, до якої приєднано тіло 2 масою m = 1 кг. До барабана прикладена пара сил з моментом М = 2 Н·м, під дією якої тіло 2 пересувається по шорсткій поверхні. Визначити пришвидшення тіла 1, якщо момент інерції барабана 1 відносно осі обертання J1 = 0,1 кг·м2, а коефіцієнт тертя ковзання f =0,1.
6.1.8 Визначити кутове пришвидшення e1 шківа 1, якщо задані радіуси шківів r1 =0,05 м, r2 =0,1 м, моменти інерції відносно осей обертання J1 =0,01кг·м2, J2 =0,02кг·м2, момент пари сил М = 0,15 Н·м.
6.1.9 Визначити кутове пришвидшення e1 зубчастого колеса 1, якщо радіуси коліс r1 =0,1 м, r2 =0,2 м, моменти інерції відносно осей обертання J1 = 0,02 кг·м2, J2 = 0,04 кг·м2, момент пари сил М = 0,3 Н·м.
6.1.10 Визначити кутове пришвидшення e2 зубчаcтого колеса 2, якщо радіуси коліс r1 =0,15 м, r2 =0,3 м, моменти інерції відносно осей обертання J1 =0,03 кг·м2, J2 =0,06 кг·м2, момент пари сил пришвидшення колеса 1 - М1 =0,4Н·м, а момент пари сил опору колеса 2 - М2 =0,08Н·м.
6.1.19 Визначити пришвидшення, з яким піднімається тіло 1 масою 10 кг під дією сили F, модуль якої 110 Н. При обчисленні приймати пришвидшення вільного падіння тіла g = 10 м/с2.
6.1.20 Визначити пришвидшення тіла 1 масою 1 кг, що піднімається по шорсткій похилій поверхні під дією сили F, модуль якої дорівнює 6,75 Н. Коефіцієнт тертя ковзання f = 0,1. в)» 1,0 м/с2; 6.1.25 З яким пришвидшенням підніматиметься тіло 1 під дією пари сил з сталим моментом М = 4,52 Н·м, якщо маси тіл m1 = m2 = 2 кг, радіус барабана r =0,2 м, який можна вважати однорідним циліндром. в)» 1,0 м/с2; 6.1.27 Визначити пришвидшення тіла 1 масою m1 =1кг, що рухається під дією моменту пари сил з модулем М = 5 Н·м. Момент інерції барабана 2 відносно осі обертання J2 = 1,0 кг·м2, радіус r = 0,5 м. д) 2,0 м/с2. Загальні теореми динаміки
2.2 Теорема про рух центра мас 2.2.1 Визначити абсцису Хс центра мас кривошипно-повзунного механізму при кутах j =900 і a = 300, якщо маса кривошипа 1 дорівнює 4 кг, а маса шатуна 2 дорівнює 8 кг. Шатун 2 довжиною 0,8 м вважати однорідним стрижнем. Масою повзуна 3 нехтуємо.
2.2.2 Визначити координату Yс центра мас кривошипно-повзунного механізму при кутах j =900 і a = 300, якщо маса кривошипа 1 дорівнює 4 кг, а маса шатуна 2 дорівнює 8 кг. Шатун 2 довжиною 0,8 м та кривошип 1 вважати однорідними стрижнями. Масою повзуна 3 нехтуємо.
2.2.3 Визначити абсцису Хс центра мас кривошипно-повзунного механізму при кутах j =900 і a = 300, якщо маса кривошипа 1 дорівнює 6 кг, а маса шатуна 2 дорівнює 10 кг. Шатун 2 довжиною 1 м та кривошип 1 вважати однорідними стрижнями. Маса повзуна зосереджена в т. В і дорівнює 2кг.
Теорема про зміну кількості руху
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.228.162 (0.011 с.) |


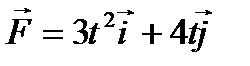 (Н). Визначити проекцію імпульсу сили на вісь ОХ за проміжок часу від 0 до 2 с.
(Н). Визначити проекцію імпульсу сили на вісь ОХ за проміжок часу від 0 до 2 с.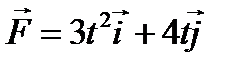 (Н). Визначити проекцію імпульсу сили на вісь ОУ за проміжок часу від 0 до 2с.
(Н). Визначити проекцію імпульсу сили на вісь ОУ за проміжок часу від 0 до 2с.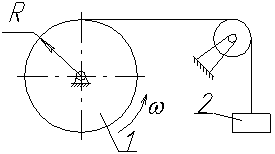
 м.
м.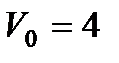 м/с. Визначити, через який час тіло досягне максимальної висоти підйому.
м/с. Визначити, через який час тіло досягне максимальної висоти підйому.
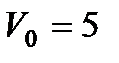 м/с, опускається по гладким похилим напрямним. Визначити, через який час швидкість цього тіла досягне величини 9,81м/с.
м/с, опускається по гладким похилим напрямним. Визначити, через який час швидкість цього тіла досягне величини 9,81м/с.
 м/с, ковзає по шорсткій горизонтальній площині і зупиняється через 1с. Визначити коефіцієнт тертя ковзання.
м/с, ковзає по шорсткій горизонтальній площині і зупиняється через 1с. Визначити коефіцієнт тертя ковзання.
 м/с піднімалось по шорсткій похилій площині і зупинилось. Визначити час руху до зупинки, якщо коефіцієнт тертя ковзання f =0,1.
м/с піднімалось по шорсткій похилій площині і зупинилось. Визначити час руху до зупинки, якщо коефіцієнт тертя ковзання f =0,1.
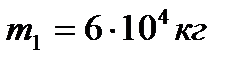 ,
, 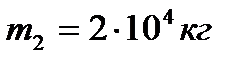 і швидкостями
і швидкостями  м/с;
м/с; 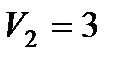 м/с. Другий вагон наздоганяє перший і зчіпляється з ним. Нехтуючи опором руху, визначити швидкість вагонів після зчеплення.
м/с. Другий вагон наздоганяє перший і зчіпляється з ним. Нехтуючи опором руху, визначити швидкість вагонів після зчеплення.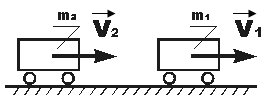
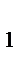 = 10кг обертається з кутовою швидкістю w = 20 рад/с. Вантаж 2 має масу m
= 10кг обертається з кутовою швидкістю w = 20 рад/с. Вантаж 2 має масу m 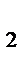 = 5кг. Визначити кінетичний момент механічної системи відносно осі обертання.
= 5кг. Визначити кінетичний момент механічної системи відносно осі обертання.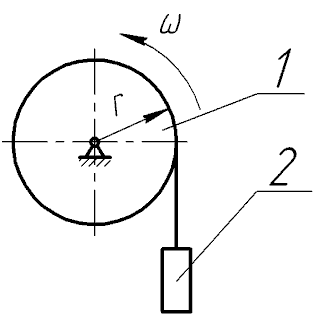
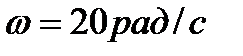 . Його момент інерції відносно осі обертання
. Його момент інерції відносно осі обертання 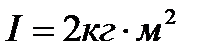 , радіус
, радіус 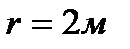 . Вантаж 2 має масу
. Вантаж 2 має масу 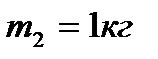 . Визначити кінетичний момент механічної системи відносно осі обертання.
. Визначити кінетичний момент механічної системи відносно осі обертання.
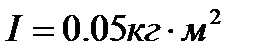 , намотані нитки, до яких прикріплені вантажі 1 і 3 масами
, намотані нитки, до яких прикріплені вантажі 1 і 3 масами  . Визначити кінетичний момент механічної системи відносно осі обертання, якщо кутова швидкість
. Визначити кінетичний момент механічної системи відносно осі обертання, якщо кутова швидкість 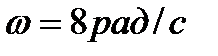 , радіуси
, радіуси 


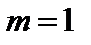 кг. Визначити кінетичну енергію тіла в момент часу, коли воно пройшло шлях
кг. Визначити кінетичну енергію тіла в момент часу, коли воно пройшло шлях  м, якщо коефіцієнт тертя ковзання між тілом і похилою площиною
м, якщо коефіцієнт тертя ковзання між тілом і похилою площиною 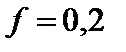 .
.
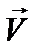 матиме вантаж, коли від початку руху пройде шлях
матиме вантаж, коли від початку руху пройде шлях 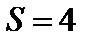 м. Коефіцієнт тертя ковзання між вантажем і похилою площиною
м. Коефіцієнт тертя ковзання між вантажем і похилою площиною 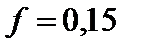 .
.
 необхідно надати однорідному стрижню довжиною
необхідно надати однорідному стрижню довжиною  м, щоб він обертаючись навколо горизонтальної осі О здійснив півоберта?
м, щоб він обертаючись навколо горизонтальної осі О здійснив півоберта?
 рад/с. Момент інерції тіла відносно осі обертання
рад/с. Момент інерції тіла відносно осі обертання  кг×м2. На який кут повернеться тіло до зупинки під дією постійного моменту тертя в підшипниках
кг×м2. На який кут повернеться тіло до зупинки під дією постійного моменту тертя в підшипниках 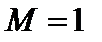 Н×м.
Н×м.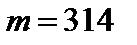 кг і радіусом інерції відносно осі обертання рівним 1м, надана кутова швидкість
кг і радіусом інерції відносно осі обертання рівним 1м, надана кутова швидкість 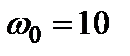 рад/с. Представлений самому собі, він зупинився через 100 обертів. Визначити момент тертя в підшипниках, вважаючи його постійним.
рад/с. Представлений самому собі, він зупинився через 100 обертів. Визначити момент тертя в підшипниках, вважаючи його постійним. м і масою
м і масою 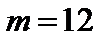 кг. Валу надана кутова швидкість
кг. Валу надана кутова швидкість  рад/с. Представлений самому собі, він зупинився через 20 обертів. Визначити момент тертя в підшипниках, вважаючи його постійним.
рад/с. Представлений самому собі, він зупинився через 20 обертів. Визначити момент тертя в підшипниках, вважаючи його постійним.
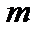 і довжиною
і довжиною  та однорідний стрижень 2 масою
та однорідний стрижень 2 масою  і довжиною
і довжиною 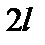 відпускають без початкової швидкості із заданих на рисунку положень. Швидкість центра мас якого тіла буде більша в нижньому положенні?
відпускають без початкової швидкості із заданих на рисунку положень. Швидкість центра мас якого тіла буде більша в нижньому положенні?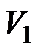 ;
;
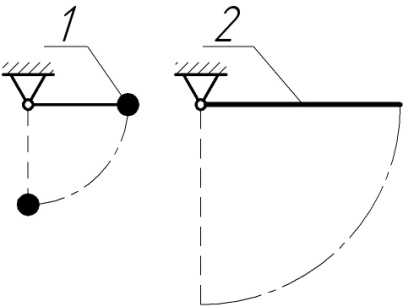
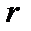 вкочується вгору без ковзання на похилу площину з початковою швидкістю центра диска
вкочується вгору без ковзання на похилу площину з початковою швидкістю центра диска 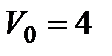 м/с. Визначити шлях, який пройде центр диска до зупинки.
м/с. Визначити шлях, який пройде центр диска до зупинки.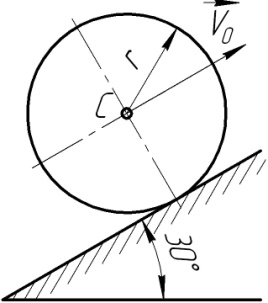
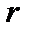 і масою
і масою  , який можна прийняти за суцільний однорідний циліндр, скотили з пагорба висотою
, який можна прийняти за суцільний однорідний циліндр, скотили з пагорба висотою 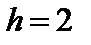 м з положення І. Визначити швидкість центра мас стовбура С в положенні ІІ, якщо швидкість точки С в положенні І дорівнювала нулю.
м з положення І. Визначити швидкість центра мас стовбура С в положенні ІІ, якщо швидкість точки С в положенні І дорівнювала нулю.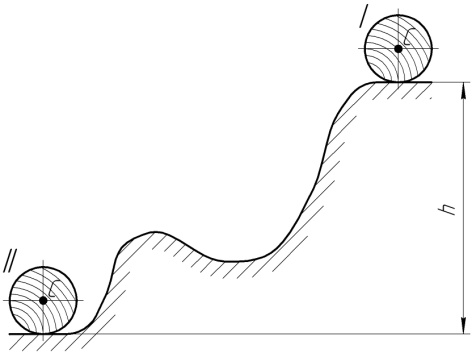
 і
і 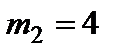 кг. Визначити пришвидшення вантажів.
кг. Визначити пришвидшення вантажів.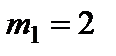 кг і
кг і  кг підвішені до кінців гнучкої нитки, перекинутої через блок. Визначити швидкість вантажу 1 в момент часу, коли він опускається на висоту
кг підвішені до кінців гнучкої нитки, перекинутої через блок. Визначити швидкість вантажу 1 в момент часу, коли він опускається на висоту  м. Рух вантажів починається зі стану спокою.
м. Рух вантажів починається зі стану спокою.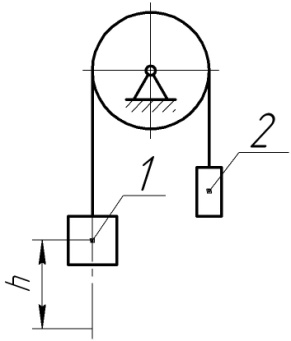
 з’єднані між собою гнучкою ниткою, рухаються по горизонтальній площині маючи початкову швидкість
з’єднані між собою гнучкою ниткою, рухаються по горизонтальній площині маючи початкову швидкість 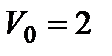 м/с. Визначити коефіцієнт тертя ковзання, якщо тіла зупиняться, пройшовши шлях 4м.
м/с. Визначити коефіцієнт тертя ковзання, якщо тіла зупиняться, пройшовши шлях 4м.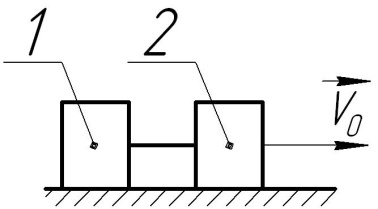
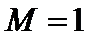 Н×м. Визначити кутову швидкість коліс після того, як вони здійснять два оберти. Радіуси інерції кожного колеса відносно осі обертання дорівнюють 0,2м.
Н×м. Визначити кутову швидкість коліс після того, як вони здійснять два оберти. Радіуси інерції кожного колеса відносно осі обертання дорівнюють 0,2м.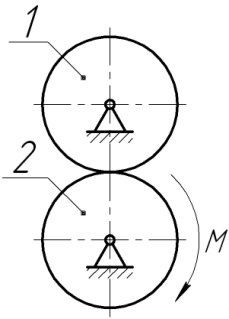
 Н×м. Моменти інерції шківів відносно їхніх осей обертання
Н×м. Моменти інерції шківів відносно їхніх осей обертання 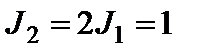 кг×м2. Визначити кутову швидкість шківа 1 після трьох обертів, якщо радіуси шківів
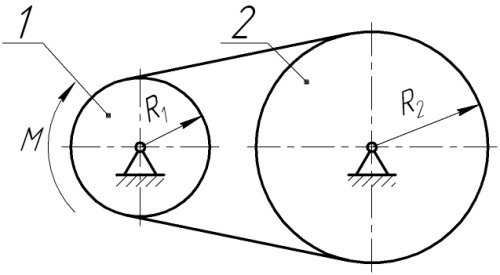
кг×м2. Визначити кутову швидкість шківа 1 після трьох обертів, якщо радіуси шківів 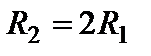 .
.
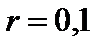 м. Загальна маса рейки 2 і вантажу 3 дорівнює 100кг. Визначити швидкість рейки при її переміщенні на віддаль
м. Загальна маса рейки 2 і вантажу 3 дорівнює 100кг. Визначити швидкість рейки при її переміщенні на віддаль  м, якщо в початковий момент система знаходилася в стані спокою.
м, якщо в початковий момент система знаходилася в стані спокою.
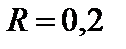 м кожний приводяться в рух зі стану спокою моментом пари сил
м кожний приводяться в рух зі стану спокою моментом пари сил 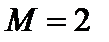 Н×м. Визначити швидкість осей котків в момент часу, коли їхні переміщення відповідають відстані 3м.
Н×м. Визначити швидкість осей котків в момент часу, коли їхні переміщення відповідають відстані 3м.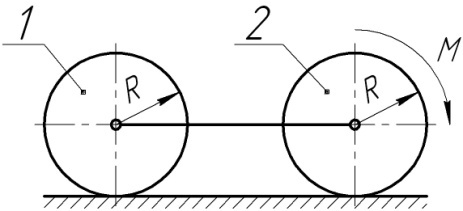
 Н×м. Після трьох обертів шківи 1 і 2 мають кутову швидкість
Н×м. Після трьох обертів шківи 1 і 2 мають кутову швидкість 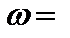 2 рад/с. Визначити момент інерції одного із шківів, коли їхні радіуси і маси одинакові.
2 рад/с. Визначити момент інерції одного із шківів, коли їхні радіуси і маси одинакові.
 ,
, 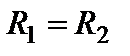 , є однорідними дисками і починають рух зі стану спокою під дією сили ваги блока 1. Визначити швидкість центра С блока 1 після того, як він опуститься вниз на відстань
, є однорідними дисками і починають рух зі стану спокою під дією сили ваги блока 1. Визначити швидкість центра С блока 1 після того, як він опуститься вниз на відстань  м.
м.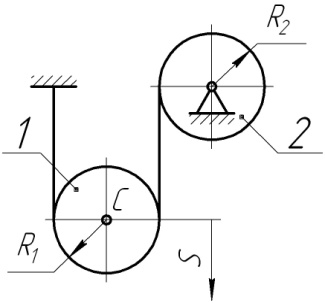
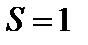 м.
м.