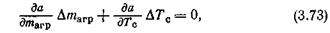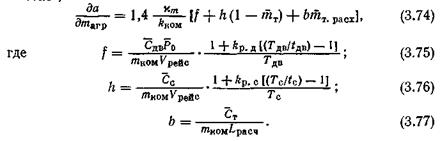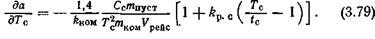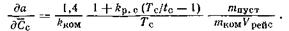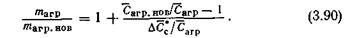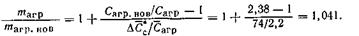Весовая и экономическая оценка проектных и конструкторских решений

Как и прежде, при использовании метода градиентов взлетной массы самолета принимаем (L, m_ц.н, V_кpeйc) = const, что позволяет упростить оценку проектных и конструкторских решений. В основе такой оценки лежит понятие о весовых эквивалентах различных величин.

Весовые эквиваленты и условия целесообразности проектных и конструкторских решений. Известно, что улучшение одних характеристик проектируемого самолета (например, аэродинамического качества, удельного часового расхода топлива, ресурса и т.п.) нередко достигается лишь ценою ухудшения других (например, весовых характеристик, стоимости и т.п.). В этом случае в процессе проектирования требуется найти границу целесообразности улучшения одних параметров за счет ухудшения других.

Две величины будем считать эквивалентными, если одновременное их изменение приводит к равному по величине, но противоположному по знаку изменению критерия оценки самолета (т.е. не приводит к изменению критерия оценки). Аналитически эквивалентность величин можно выразить так:

(3.52)

где а – критерий оценки самолета; i – число параметров.

Рассмотрим весовые эквиваленты следующих наиболее характерных параметров самолета:

– аэродинамического качества;

– силы лобового сопротивления;

– коэффициента лобового сопротивления С_х0;

– стоимости самолета;

– ресурса самолета.

Условия получения перечисленных весовых эквивалентов, вытекающие из формулы (3.52), следующие (в том же порядке):

Dа_m + Δa_Κ = 0; (3.53)

Dа_m + Δа_Χ0 = 0; (3.54)

Dа_m + Δа_Сχ0 = 0; (3.55)

Dа_m + Δа_Сс, = 0; (3.56)

Dа_m + Δа_Тс = 0. (3.57)

Очевидно, что проектно-конструкторское решение целесообразно, если оно приводит к улучшению критерия оценки самолета.

Ради простоты будем считать, что для осуществления того или иного конструкторского решения не требуются или требуются весьма малые затраты в виде дополнительных капиталовложений.

Рассмотрим, как определяются приведенные выше весовые эквиваленты основных характеристик самолета.

Весовые эквиваленты аэродинамического качества. Противоречия между массой и аэродинамическим качеством, массой и сопротивлением воздуха не новы. Они возникли вместе с первыми самолетами. Сущность противоречий состоит в том, что уменьшение сопротивления агрегатов и деталей самолета, находящихся в потоке, может быть достигнуто, как правило, лишь за счет увеличения массы. Поэтому логичным является вопрос: на какое увеличение массы следует идти для определенного увеличения аэродинамического качества или уменьшения сопротивления?

Задача нахождения весового эквивалента аэродинамического качества самолета формулируется следующим образом. Допустим, что для увеличения аэродинамического качества самолета требуется увеличить массу детали, узла или агрегата. Найти рациональный предел увеличения массы частей самолета для увеличения аэродинамического качества (Здесь имеется в виду среднее за полет аэродинамическое качество самолета. Заметим, что возможна и обратная формулировка: с помощью какого уменьшения массы детали, узла или агрегата можно компенсировать уменьшение аэродинамического качества самолета?), при котором величина критерия оценки самолета остается неизменной.

Если для простоты считать, что изменения массы и аэродинамических характеристик не влияют на стоимость и ресурс какого-либо узла или агрегата, то при (L, m_ц.н, V_крейс) = const критерием оценки проектных решений будет величина изменения взлетной массы.

В этом случае весовой эквивалент аэродинамического качества выражается так:

(Dm₀)_m + (Dm₀)_К = 0. (3.58)

Здесь (Dm₀)_m – прирост взлетной массы самолета в связи с изменением массы узла или детали; (Dm₀)_К – прирост взлетной массы в связи с изменением аэродинамического качества самолета. Если учесть, что

(Dm₀)_m = c_mDm_доп; (Dm₀)_К = c_К DК,

то из (3.58) получим, что весовой эквивалент среднего за время полета аэродинамического качества самолета

Dm_доп = –(c_К/c_m) ΔΚ. (3.59)

Когда требуется получить прирост среднего аэродинамического качества (+DК), то по формуле (3.59) получаем +Dm_доп так как производная c_К всегда отрицательна.

При решении обратной задачи, когда требуется найти, насколько следует снизить массу детали, узла или агрегата для компенсации уменьшения качества (–DК), формула (3.59) дает рациональный минимум снижения массы со знаком минус (–Dm_доп).

Если формулу (3.59) записать в виде неравенства

Dm_доп >< –(c_К/c_m)DК, (3.60)

то получим условие целесообразности проектно-конструкторского решения. Знак «меньше» соответствует прямой задаче (+DК), а знак «больше» – обратной задаче (–DК). Из неравенства (3.60) следует, что если увеличение среднего аэродинамического качества связано с увеличением массы детали, узла или агрегата, то величина Dm_доп должна быть меньше, чем (çc_Кú/c_m)DК Аналогичное рассуждение можно провести и в отношении обратной задачи.

При сравнении нескольких вариантов решения критерием их выгодности будет величина снижения взлетной массы самолета

Dm₀ = c_mDm_доп + c_КDК. (3.61)

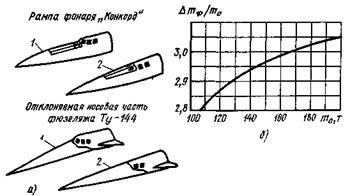
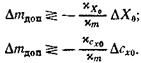
Рис. 3.3. Варианты изменяемой геометрии носовой части фюзеляжа:

а – схемы изменения геометрии носовой части фюзеляжа (1 – при Μ < 1; 2 – при Μ > 1);

б – зависимость наибольших допустимых потерь массы фюзеляжа, связанных с изменением геометрии его носовой части (М_расч = 2,2; m_ком = 13,5т; DК = 0,64),от m₀.

Здесь Dm_доп и DК – фактические приращения массы агрегата и среднего аэродинамического качества самолета.

Сумма (3.61) является отрицательной, так как производная c_К всегда отрицательна, а |c_КDК| > |c_mDm_доп| (в прямой задаче +DК, +Dm_доп). В обратной задаче сумма (3.61) также отрицательна, потому что Dm_доп и DК имеют знак минус, а |c_mDm_доп| > |c_КDК|.

Решение будет наивыгоднейшим при (–Dm₀)_max.

Пример. Продувками установлено, что аэродинамическое качество сверхзвукового пассажирского самолета (СПС) при конфигурации носовой части фюзеляжа 2 (рис. 3.3) на 0,64 единицы выше в крейсерском полете, чем при конфигурации 1, соответствующей взлету – посадке. Устройство специальной рампы, закрывающей фонарь при М> 1, или механизмов для отклонения носовой части фюзеляжа (для улучшения обзора) требует определенных весовых затрат.

Необходимо определить максимально допустимую дополнительную массу фюзеляжа, компенсируемую увеличением аэродинамического качества СПС. Иначе говоря, требуется определить весовой эквивалент увеличения аэродинамического качества СПС на 0,64 единицы.

Будем считать, что средний за полет прирост качества также равен 0,64 единицы.

Решим пример, касающийся СПС с М_расч = 2,2.

Чтобы получить весовой эквивалент прироста качества на 0,64 единицы, воспользуемся формулой (3.59) и данными табл. 3.2 и 3.3. В результате получим максимально допустимый прирост массы фюзеляжа Δm_ф = Dm_агр = Dm_доп при устройстве рампы или системы поворота носовой части фюзеляжа. Относительная масса (Dm_ф/Dm₀)_{mах доп} составляет около 3 %. По приближенной оценке потребное увеличение массы фюзеляжа СПС не превысит 0,5...0,7 % от взлетной массы СПС. Поэтому уже на стадии эскизного проектирования, не производя сложных вычислений, можно сделать вывод о целесообразности рассмотренного конструктивно-проектировочного решения.

Весовые эквиваленты лобового сопротивления и коэффициента С_х0 самолета, Задача формулируется так: насколько можно увеличить массу агрегата, узла или детали для уменьшения силы лобового сопротивления самолета или коэффициента С_х0 с тем, чтобы величина критерия оценки самолета не изменилась?

В этой формулировке задачу условно назовем прямой, в отличие от обратной, которая формулируется иначе: насколько надо уменьшить массу агрегата, узла или детали, чтобы компенсировать увеличение силы лобового сопротивления самолета или ее коэффициента С_х0?

Здесь средние за полет значения силы лобового сопротивления Х₀ и коэффициента лобового сопротивления С_х0 можно найти по следующим формулам:

Эти формулы применяются в основном для сверхзвуковых самолетов, у которых Х₀ и С_х0 существенно отличаются при Μ < 1 и Μ > 1. Что касается дозвуковых неманевренных самолетов, то без ущерба для точности определения весовых эквивалентов можно принимать (Х₀)_ср = (Х₀)_крейс, а также (С_х0)_ср = (С_х0)_крейс, так как полет этих самолетов от взлета до посадки ведется практически на режиме q» const. В дальнейшем ради краткости записи индексы «ср» и «крейс» опускаются.

Как и прежде, будем считать, что (L, m_ц.н, V) = const. Тогда условия (3.54) и (3.55) для получения весовых эквивалентов силы Х₀ и коэффициента С_х0 будут иметь вид

(Dm₀)_m + (Dm₀)_X0 = 0; (3.64)

(Dm₀)_m + (Dm₀)_Cх0 = 0, (3.65)

или, по аналогии с предыдущим,

cDm_доп + χ_Х0ΔΧ₀ = 0; (3.66)

cDm_доп + χ_Сх0ΔС_Χ0 = 0. (3.67)

Из уравнений (3.66) и (3.67) получим искомые весовые эквиваленты:

– весовой эквивалент силы Х₀

Dm_доп = –(χ_Х0/χ_m)DХ₀; (3.68)

– весовой эквивалент коэффициента С_х0

Dm_доп = –(χ_Сх0/χ_m)DC_Х0 (3.69)

При решении прямой задачи DХ₀ и DС_х0 берутся со знаком минус, а Dm_доп по формулам (3.68) и (3.69) получается со знаком плюс, так как χ_Х0, χ_Сх0 и χ_m всегда положительны. При решении обратной задачи (уменьшение массы при увеличении сопротивления) имеем (+ΔΧ₀), (+ΔС_Х0) и соответственно (–Δm_доп).

Если (3.68) и (3.69) записать в виде неравенств, то получим условия целесообразности проектно-конструкторских решений:

Знак «меньше» соответствует прямой задаче (–ΔХ₀), а знак «больше» – обратной задаче (+ΔХ₀).

Приращение ΔХ₀ равно [(ΔС_Х0) S_i]q, где S_i – характерная площадь, к которой отнесено приращение ΔС_Х0. Так как (ΔС_Х0)S_i = const и q = const, то численное значение ΔХ₀ не изменится от того, отнесено ΔХ₀ к агрегату, узлу, детали или к самолету в целом (т.е. к площади крыла).

В формуле (3.71) принято

ΔС_Х0 = ±(С_Х0)_iS_i/S,

где (С_Х0)_i – добавочный коэффициент вредного аэродинамического сопротивления агрегата, узла или детали, отнесенный к характерной площади S_i, S – площадь крыла.

При сравнении нескольких вариантов решений наилучшим будет вариант, который дает наибольшее снижение взлетной массы:

Δm₀ = (c_mΔm_доп + c_Х0ΔХ₀)_mах. (3.72)

Здесь сумма c_mΔm_доп + c_Х0ΔХ₀ всегда отрицательна при целесообразных вариантах и положительна – при нецелесообразных; Δm_доп – наибольший допустимый прирост массы агрегата, узла или детали (в кг), оправдываемый уменьшением силы Х₀ на 1 даН.

В табл. 3.4 даны значения весовых эквивалентов силы вредного аэродинамического сопротивления некоторых типов самолетов.

Таблица 3.4 Весовые эквиваленты Δm_доп силы лобового сопротивления.

Условие	Основные исходные данные
m0, кг Vкрейс, км/ч Lрасч, км
(р0, 0) = const	Δmдоп, кг	1,03	1,20	5,25	6,3	2,6
(S, Р0) = const	0,97	1,06	4,60	4,8	—

Из табл. 3.4 видно, что только на легком самолете изменение массы узла или детали на 1 кг влияет на взлетную массу самолета примерно так же, как изменение на 1 даН силы лобового сопротивления (Δm_агр/ΔХ₀» 1). На тяжелых дозвуковых самолетах изменение на 1 даН силы лобового сопротивления эквивалентно изменению массы агрегата, узла или детали на 4... 6 кг, т.е. Δm_агр/ΔХ₀ = 4... 6.

Весовые эквиваленты ресурса конструкции самолета. Определим наибольшее допустимое (по соображениям себестоимости перевозок) увеличение ресурса конструкции транспортного самолета, когда оно связано с приростом массы (например, в результате создания резервных силовых элементов, ограничителей распространения трещин, местных усилений, снижения действующих напряжений для увеличения усталостной прочности и т.п.), т.е. найдем весовой эквивалент ресурса конструкции.

Для упрощения решения полагаем, что исходная удельная стоимость самолета `С<sub>с</sub> не зависит от исходного ресурса самолета Т<sub>с</sub>, т.е. д `С_с/ д Т_с = 0.

Из условия (3.57) имеем

где а – себестоимость тонна-километра.

Производная д а/ д m_агр = д а/ д m_доп определяется следующим образом.

На ранней стадии проектирования, когда для сохранения заданных значений скорости и дальности принимается (р₀, `Р₀) = const.

Значения коэффициентов, входящих в формулы (3.75)... (3.77), указаны в разд. 3.1, размерность f, h и b – коп/(т²×км).

На более поздней стадии проектирования, когда (S, Р₀) = const

Производную д а/ д Т_с, входящую в (3.73), можно определить по формуле

Здесь С_с в коп/т; Т_с в ч; m_пуст и m_ком в т.

Подставляя значения д а/ д m_агр и д а/ д Т_с в (3.73), после преобразований получим весовые эквиваленты ресурса конструкции самолета:

при (р₀, `Ρ₀) = const

В (3.75) `С<sub>дв</sub> и в (3.76) `С_с – стоимость двигателей, отнесенная к взлетной тяге, и стоимость самолета без двигателей, отнесенная к массе пустого самолета без двигателей (в коп/т); `С_т = 5200 коп/т – удельная стоимость топлива; Т_с – исходный ресурс конструкции самолета (в ч).

Сравнив фактические затраты массы для увеличения ресурса на заданную величину DТ_с (в ч) с наибольшими допустимыми затратами, определяемыми по формулам (3.80) и (3.81), можно сделать вывод о целесообразности данного проектно-конструкторского решения.

В табл. 3.5 даны весовые эквиваленты увеличения ресурса гражданских самолетов на 1000 ч при исходном ресурсе 40000 ч. Из таблицы видно, что наибольший допустимый прирост массы конструкции агрегата с целью увеличения его ресурса при (S, Р₀) = const примерно вдвое больше, чем при (р₀, `Р₀) = const. Это объясняется меньшим влиянием массы конструкции агрегатов на себестоимость 1 т×км при (S, P₀) = const.

Таблица 3.5

Наибольший прирост массы конструкции самолета д m_агр (кг), оправдываемый увеличением ее ресурса на 1000 ч (Т_с.исх = 40000 ч)

Условие	Основные исходные данные
m0, кг Vкрейс, км/ч Lрасч, км
(р0, `Р0) = const	Dmarp, кг	10,3	24,5	42,5
(S, Р0) = const	20,3	44,5	75,0

Весовые эквиваленты стоимости конструкции самолета. При проектировании самолетов нередко приходится решать, при каких условиях целесообразно применить более легкую, но более дорогую конструкцию агрегата, узла или детали (Возможна и обратная задача, которая ставится следующим образом: при каких условиях целесообразно применить более тяжелую, но более дешевую конструкцию?). Известно, например, что монолитные фрезерованные конструкции, конструкции из титана или стеклопластиков в настоящее время значительно дороже, чем аналогичные сборные узлы, узлы из алюминиевых сплавов или стали. Однако монолитные детали, детали из дорогостоящих материалов могут дать значительную экономию массы. Это противоречие массы и стоимости приводит к необходимости определить весовой эквивалент стоимости, найти границу, разделяющую целесообразные варианты решений от нецелесообразных.

При решении данной задачи принимаем, как и раньше, (L, m_ц.н, V) = const. Считаем также, что изменение стоимости самолета не приводит к изменению ресурса его конструкции, т.е. считаем Т_с = const.

Из условия (3.56) имеем

где Dm_агр – изменение массы агрегата, узла или детали; D`С_c – изменение удельной стоимости самолета.

Производная д а/ д m_агр = д а/ д m_доп применительно к самолетам гражданской авиации определяется по формуле (3.74) при (р₀, `Р₀) = const или по формуле (3.78) при (S, Р₀) = const. Производная д а/ д С₀ определяется по формуле

Подставим значения производных в (3.56). Тогда получим абсолютное значение отношения DС_с/Dm_агр (руб./кг) при условии, что

DС_с = D_сm_пуст.

Полагая (р₀, ₀) = const, получим

В формулах (3.83) и (3.84) m_ком в т, а многочлен в квадратных скобках (в числителе) имеет размерность коп./(т²×км).

Стоимость конструкции самолета составляет по статистике 65...75 % от стоимости пустого самолета с оборудованием. Поэтому при определении дополнительной стоимости конструкции самолета, оправдываемой уменьшением ее массы на 1 кг, значения |DС_с/Dm_агр|, определяемые по формулам (3.83) и (3.84), надо умножить на коэффициент β = С_кон/С_с = 0,65...0,75. В примерах расчета будем принимать β = 0,7. Обозначим

D^*_c = |DC_c/Dm_arp|×β, (3.85)

где _агр – стоимость 1 кг исходного агрегата, узла или детали; m_агр – масса исходного агрегата, узла или детали; _{агр.нов}, m_{агр.нов} – стоимость 1 кг и масса нового агрегата, узла или детали (взамен исходных).

Рассмотрим для определенности случай, когда m_{агр.нов} <m_агр, а _{агр.нов} > _агр. Стоимость (руб.) исходной конструкции агрегата, узла или детали

C_arp = _агрm_агр (3.86)

Стоимость новой конструкции с меньшей на Dm_агр массой

C_arp.нов = _агр (m_агр – Dm_агр) + D^*_с Dm_arp, (3.87)

где D^*_c – экономия (руб.) от уменьшения массы конструкции на 1 кг.

Разделим левую и правую части (3.87) на произведение

_агрm_агр = C_arp:

Формула (3.88) определяет весовой эквивалент стоимости конструкции агрегатов, узлов или деталей самолета. Из этой формулы следует:

1) если С_{агр.нов}/С_агр > D^*_c/_arp, то снижением массы уже невозможно компенсировать увеличение стоимости агрегата, узла или детали (рис. 3.4);

2) могут быть два случая, когда для компенсации относительного увеличения стоимости новой конструкции требуется такое же по величине относительное снижение ее массы, т.е. когда

m_агр/m_{агр.нов} = C_{агр.нов}/C_агр

Кроме тривиального случая, когда

m_агр/m_{агр.нов} = C_{агр.нов}/C_агр = 1,

возможен еще такой, когда

m_агр/m_{агр.нов} = C_arp.нов/С_агр = D^*_c/_агр – 1. (3.89)

Если известны не абсолютные стоимости С_агр и С_{агр.нов}, а относительные: _агр = С_агр/m_агр и _{агр.нов} = С_{агр.нов}/m_{агр.нов}, то формула (3.88) принимает вид

Записывая формулу (3.88) в виде неравенства

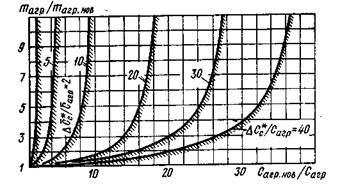
получим условие целесообразности проектно-конструкторского решения. В формуле (3.91) m_aгp/m_aгp.нов – отношение фактических значений масс новой и исходной конструкции. Зоны целесообразных решений видны из рис. 3.4.

Рис. 3.4. Зоны целесообразности применения более дорогой, но более легкой конструкции
(агрегата, детали): I – зона целесообразности конструктивного решения; II – зона нецелесообразности конструктивного решения

При решении данной задачи экономию (руб./кг) от уменьшения массы конструкции на 1 кг можно найти по следующей формуле:

D^*_c = c_m [26ξ₀ + 0,53_с (1 – m_т) + 400 (C_Р/К)_крейс], (3.92)

где ξ = 1, если (р₀, ₀) = const_; ξ = 0, если (S, Р₀) = const.

Удельная стоимость самолета _с, входящая в (3.92), находится с помощью формулы (3.8) (следует С_с разделить на m_пуст).

Для прикидочных расчетов D^*_c (руб./кг) можно пользоваться следующими простыми зависимостями:

при (р₀, ₀) = const D^*_c» 47c_m;

при (S, Р₀) = const D^*_c» 38c_m.

В заключение рассмотрим примеры, иллюстрирующие метод весовых эквивалентов стоимости конструкции.

Пример 1. Целесообразно ли детали из алюминиевого сплава Д16-Т, работающие в основном на растяжение, заменять деталями из стеклопластиков АГ-4С или ВФТ-2СТ, если последние легче на (17...25)%, но в 2,4...6,4 раза дороже?

Предполагается, что по жесткостным, усталостным и другим характеристикам указанные стеклопластики удовлетворяют требованиям, предъявляемым к конструкции.

Основные данные сравниваемых материалов приведены в табл. 3.6, где ρ – плотность; Ε – модуль упругости; σ_Β – временное сопротивление разрыву; s_0,2 – нормальное напряжение при относительном удлинении 0,2%.

Таблица 3.6 Характеристики материалов и деталей (к примеру 1)

Характеристики	Д16-Т	АГ-4С	ВФТ-2СТ
r, кг/см^3	2,8×10^–^3	1,8×10^–^3	1,9×10^–^3
E, даН/см^2	7,2×10^5	1,2×10^5	4×10^5
sB, даН/см^2	4,5×10^3	4×10^3	6×10^3
Σ0,2, даН/см^2
(σ0,2/r)×10^–^5, даНсм/кг	9,65	11,7	16,9
Стоимость материала, руб./кг	1,0	4,5
Средняя себестоимость деталей, руб./кг	2,2	5,24
Относительная себестоимость деталей, %
Относительная масса, %		82,5	70...75

Рассмотрим задачу применительно к четырем типам дозвуковых пассажирских самолетов, основные данные которых даны в табл. 3.7. Исходная удельная стоимость агрегата, узла или детали С_агр = 2,2 руб./кг (себестоимость изготовления из Д16-Т). Найдем по формуле (3.90) относительный весовой эквивалент стоимости. Например, для материала АГ-4С применительно к самолету № 1 имеем

Фактическое отношение

(m_агр/m_{агр.нов})_факт = 100/82,5 = 1,21.

Таблица 3.7

Экономия от уменьшения массы агрегата, узла или детали на 1 кг для дозвуковых пассажирских самолетов (к примеру 1)

Основные исходные данные	№ самолета
m0, кг Vкрейс, км/ч Lрасч, км
(S, Р0) = const (p0, 0) = const	D^*c, руб./кг	74,0 150,0	72,0 138,5	79,5 150,5	102,5 200,0

Результаты расчетов даны в табл. 3.8, из которой следует, что во всех рассмотренных случаях замена сплава Д16-Т стеклопластиками АГ-4С и ВФТ-2СТ целесообразна.

Если узлы или детали из стеклопластика АГ-4С будут дороже не в 2,38 раза (как в табл. 3.8), а в 8...10 раз, но легче на 17,5 % по сравнению с узлами из Д16-Т, то и в этом случае переход на стеклопластик будет оправдан.

Таблица 3.8 Результаты расчетов (к примеру 1)

Характеристика	Номер самолета
АГ-4С	ВФТ-2СТ	АГ-4С	ВФТ-2СТ
Относительный весовой экви­валент (3.90) ()факт	1,041 1,21	1,159 1,33...1,43	1,042 1,21	1,163 1,33... 1,43
Характеристика	Номер самолета
АГ-4С	ВФТ-2СТ	АГ-4С	ВФТ-2СТ
Относительный весовой эквивалент (3.90) ()факт	1,038 1,21	1,149 1,33...1,43	1,03 1,21	1,15 1,33...1,43

Пример 2. Целесообразно ли заменить болты из стали 30ХГСНА болтами из титана ВТ-14, если стоимость болтов возрастет с 2 руб./кг до 25 руб./кг, а масса их уменьшится на 26 %?

Основные характеристики рассматриваемых материалов при нормальной температуре даны в табл. 3.9.

Таблица 3.9 Характеристики материалов (к примеру 2)

Характеристики материалов	30ХГСНА	ВТ-14
r, кг/см^3 Е, даН/см^2 σΒ, даН/см^2 σ0,2, даН/см^2 (σΒ/ρ)×10^5, даНсм/кг (σ0,2/ρ)×10^–5, даНсм/кг	7,85 21×10^5 22,9 12,1	4,52 11×10^5 28,8

Предполагается, что удельная усталостная прочность титановых болтов не хуже, чем стальных.

Возьмем для примера те же типы дозвуковых самолетов, что и в предыдущем примере (см. табл. 3.7). Тогда _агр = 2 руб./кг; _{агр.нов} =25 руб./кг, m_агр/m_{агр.нов} = 1,35.

Определим далее по формуле (3.88) минимально допустимое отношение массы стальных и титановых болтов (m_с.б/m_т.б)_min

Результаты расчета таковы:

Номер самолета 1 2 3 4

(m_с.б/m_т.б)_min 1,311 1,318 1,290 1,225

Так как фактическое отношение масс в 1,35 раза больше, чем минимально допустимое для всех рассматриваемых типов самолетов, то можно сделать вывод о целесообразности применения титановых болтов, исходя из рассмотрения противоречия масса – стоимость (если D^*_c = 115 руб./кг).

Следует подчеркнуть, что полезный эффект будет тем больше, чем раньше реализуется его внедрение в процессе проектирования.

Применение нелегированного титана (например, ОТ-4-1) в качестве жаропрочного материала вместо стали в несиловых конструкциях (выхлопные трубы, противопожарные перегородки, трубопроводы обогрева и т.п.) еще более оправданно, чем применение силовых титановых конструкций, так как несиловые титановые конструкции, хотя они и значительно дороже, получаются примерно вдвое легче стальных.

Пример 3. Целесообразно ли пол пассажирской кабины из алюминиевого сплава Д-16Т заменять на пол из углепластика, если он будет вдвое легче, но в 10 раз дороже? _

Допустим, что _агр = 5 руб./кг и _{агр.нов} = 50 руб./кг. Проделав те же операции, что и в предыдущем примере, получим ответ: если D^*_c ³ 100 руб./кг, то замена целесообразна.

Пример 4. Целесообразно ли в колесных тормозах тяжелых пассажирских самолетов применять бериллиевый сплав взамен стали, если при этом конструкция будет вдвое легче, но в 65 раз дороже?

Исходные данные: _агр = 2 руб./кг; _{агр.нов} = 130 руб./кг; _{агр.нов}/_агр» С_{агр.нов}/С_агр = 65; D^*_c = 440 руб./кг.

Пользуясь формулой (3.88) получим, что замена стали на бериллий в данном примере оправдана. Однако для самолетов с взлетной массой £ 200т, у которых D^*_c < 250...260 руб./кг, такая замена нецелесообразна (если нет уверенности в снижении стоимости бериллиевого сплава ко времени постройки самолета).