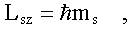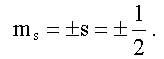Объяснение температурной зависимости теплоемкостей газов

В части 4, лекции N 4 обсуждались графики экспериментальных зависимостей теплоемкости C_V для двух газов: одноатомного аргона (Ar) и двухатомного водорода (H₂). Ход графика для аргона соответствовал предсказаниям классической теории теплоемкости: у одноатомного газа три степени свободы (i = 3), соответственно C_V = (i/2)R = (3/2)R во всем диапазоне температур. Двухатомный водород имеет i = 7 (3 поступательные, 2 вращательные, 2 колебательные степени свободы, см., классическая теория дает для него значение C_V = (7/2)R. Однако, как показывает опыт, водород ведет себя как газ с переменным числом степеней свободы. Они как бы "вымораживаются": при низких температурах i = 3, затем при T > 100K число степеней свободы плавно(!) увеличивается и достигает 5 при T ≈ 400K. Затем до T ≈ 800K число степеней свободы остается постоянным, а дальше опять плавно растет до значения i = 7.

Такое поведение теплоемкости становится понятным если учесть квантование вращательного и колебательного движений молекулы. Поступательное движение не квантуется и его вклад в теплоемкость (i = 3) присутствует всегда. При низких температурах, когда средняя энергия теплового движения молекулы (ε ~ kT) меньше, чем квант энергии вращательного движения (см. схему уровней в предыдущем параграфе), тепловое движение не способно возбудить вращение молекулы и она ведет себя как частица без внутренней структуры с числом степеней свободы i = 3. Затем, с ростом T, у наиболее энергичных молекул начинают возбуждаться вращательные степени свободы, этим объясняется плавный рост теплоемкости, соответствующий появлению нецелых значений числа i. Колебательные степени свободы возбуждаются при более высоких температурах, т.к. расстояние между колебательными уровнями значительно больше, чем расстояние между вращательными.

Итоги лекции N 9

1. Электрон обладает собственным моментом импульса L_S, не связанным с движением в пространстве. Модуль собственного момента импульса определяется спиновым квантовым числом S (см. (9.1)):

2. Проекция спина на ось z L_Sz квантуется (см. (9.2)):

здесь m_s - магнитное спиновое квантовое число, для электрона (см. (9.3)):

3. Квантовое состояние электрона в любом атомезадается четырьмя квантовыми числами:

4. Частицы с полуцелым спином s относятся к фермионам (например - электрон), а частицы с целым спином - к бозонам (например - фотон).

5. Принцип Паули утверждает, что в квантовой системе фермионов две частицы не могут находиться в одном и том же квантовом состоянии.

6. Бозоны не подчиняются принципу Паули, они могут находиться в одинаковом квантовом состоянии в неограниченном количестве.

7. Периодическое повторение химических свойств элементов с ростом зарядового числа Z, открытое Д.И. Менделеевым, объясняется заполнением электронами квантовых состояний в атоме с учетом принципа Паули.

8. В молекулах различают два типа связи: ковалентную и полярную.

9. Ковалентная связь осуществляется за счет обобществления электронов, принадлежащих двум атомам.

10. Ионная связь обусловлена переходом электронов с одного атома на другой с образованием положительных и отрицательных ионов с электростатическим притягиванием между ними.

11. Энергия изолированной молекулы может быть приближенно представлена в виде:

здесь E_эл - электронная энергия, она обусловлена электронной конфигурацией в молекуле; E_кол - энергия колебания ядер относительно центра масс молекулы E_вр - энергия вращения ядер относительно центра масс молекулы.

Порядки величин E_эл, E_кол и E_вр следующие:

E_эл ~ 1 ÷10 эВ;

E_кол ~ 10^-2 ÷10^-1 эВ;

E_вр ~ 10^-5 ÷10^-3 эВ.

12. Квантование колебательной и вращательной энергии молекулы объясняет экспериментально наблюдаемую зависимость теплоемкостей газов от температуры (см. § 4).

 

КВАНТОВАЯ ТЕОРИЯ СВОБОДНЫХ ЭЛЕКТРОНОВ В МЕТАЛЛЕ

 

ЛЕКЦИЯ N 10

Электронный газ в модели одномерной бесконечно глубокой потенциальной ямы. Электронный газ в модели бесконечно глубокой трехмерной потенциальной ямы

Валентные электроны в металле могут довольно свободно перемещаться в пределах объема металлического образца. Потенциальная энергия электрона в пределах образца металла приблизительно постоянна, но для выхода электрона из металла надо совершить работу против сил электростатического притяжения отрицательного электрона к ионному остатку.

Таким образом, валентные электроны металла находятся в потенциальной яме. Глубина этой ямы - работа выхода электронов из металла A - составляет несколько электронвольт. При низких температурах, когда тепловое движение не способно удалить электрон из металла, потенциальную яму можно считать бесконечно глубокой. Мы начнем рассмотрение поведения свободных (валентных) электронов в металле с самой простой модели: модели одномерной бесконечно глубокой потенциальной ямы при T = 0. Затем обобщим результаты на случай более реалистичной модели бесконечно глубокой трехмерной ямы. После чего рассмотрим поведение свободных электронов в металле (электронный газ) при T > 0, для чего нам потребуются элементы квантовой статистики Ферми-Дирака.