Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунково–графічний аналіз результатів експерименту
1. За даними вимірів п.3 визначити активні R, реактивні X та повні опори Z і кути зсуву j, а також комплексні 2. Для електричного кола рис. 6.1 побудувати топографічну діаграму. 3. За даними вимірів п.6 визначити активні G, реактивні B та повні провідності Y і кути зсуву, а також комплексні 4. Для електричних кіл на рис. 6.1, рис. 6.2 побудувати векторні діаграми.
Таблиця 6.4
Таблиця 6.5
5. Для кожного з електричних кіл рис.6.3 та 6.4 побудувати топографічну діаграму напруг, суміщену з векторною діаграмою струмів. 6. Вважаючи відомими параметри елементів (див. таблицю 6.4), розрахувати струми віток електричних кіл (рис. 6.1-6.4) та їхні активні потужності; порівняти результати розрахунків з результатами експериментальних вимірів. 7. Зробити і записати у протоколі звіту висновки по роботі.
Стислі теоретичні відомості
Методичні вказівки
Миттєве значення синусоїдного струму записують так: i = Imsin(wt + yi), де Іm - амплітудне значення струму; (wt + yi) - фаза; yi - початкова фаза (значення фази в момент часу t = 0); w = 2 pf - кутова частота; f = 1/Т - циклічна частота; Т - період. Крім миттєвих та амплітудних значень, часто використовують діючі значення струмів та напруг I=Im/√2; U=Um/√2
Від струму i = Imsin(wt + yi), що тече в електричному колі з послідовним сполученням R, L і С, на окремих ідеальних елементах та вхідних затискачах, створюються напруги: uR = R×i = R×Imsin(wt + yi);
u = uR + uL + uC = Umsin(wt + yu) = Z × Imsin(wt + yu).
Як видно з наведених рівнянь, для кожного елемента і для кола в цілому виконується закон Ома стосовно амплітудних значень:
Розділивши обидві частини кожної з цих формул на √2, одержимо закон Ома для діючих значень
Стосовно миттєвих значень закон Ома дійсний тільки для резистора. Для індуктивності, ємності
(заважає доданок ± π/2 в початковій фазі). Для кола в цілому в загальному випидку Напруга на резисторі uR має таку ж початкову фазу, що і струм. Напруга на індуктивності uL випереджає струм за фазою на кут p/2, а напруга на ємності uc відстає за фазою від струму на кут p/2. Кут зсуву фази визначають як різницю початкових фаз напруги та струму, тобто j = yu - yi. Якщо j > 0, то напруга випереджає струм, що свідчить про індуктивний характер електричного кола. В разі j < 0, струм випереджає напругу, і таке електричне коло має ємнісний характер. Кут зсуву фаз між напругою та струмом на вхідних затискачах електричного кола залежить від параметрів всіх елементів кола, і його визначають за формулою: j = arctg [(XL – XC) / R]. Величину XL = wL називають індуктивним реактивним опором, або індуктивним реактансом, ХС = 1/wC - ємнісним реактивним опором або ємнісним реактансом. Різниця індуктивного та ємнісного реактансів (X = ХL– ХC) називають реактивним опором електричного кола або реактансом кола. На відміну від реактивних опорів індуктивності та ємності опір резистора R називають активним опором. Z – повний опір електричного кола. Зв’язок між активним, реактивним і повним опорами наочно ілюструється трикутником опорів (рис 6.5). З трикутника опорів зокрема видно:
Якщо електричне коло складається з елементів R, L i С, сполучених паралельно, то для його розрахунку користуються поняттям провідності, що є величиною, оберненою відповідному опору. В такому разі розглядають:
сусцептанс);
кола), що є різницею індуктивного та ємнісного сусцептансів.
Кут зсуву фаз між напругою та струмом на вхідних затискачах електричного кола також залежить від параметрів всіх елементів кола і його визначають за формулою:
j = arctg [(BL – BC) / G]
Закон Ома для кожного з елементів (стосовно діючих значень):
IR=U/R=UG; IL=U/XL=UBL; IC=U/XC=UBC.
Закон Ома для кола в цілому: I=U∙Y, де Y – повна провідність (адмітанс) паралельного кола. Зв’язок між активною, реактивною і повною провідностями наочно ілюструється трикутником провідностей (рис.6.6). З трикутника провідностей зокрема видно:
В стислих теоретичних відомостях поки що йшлося про кола, складені з ідеальних елементів R, L, C. Лабораторні стенди містять звичайно не ідеальні, а реальні пристрої – резистор, котушку, конденсатор, які й використовуються для дослідження. Кожний з цих пристроїв, як і будь-який пасивний двополюсник, може бути поданий однією з схем заміщення (рис. 6.7. б, в). Послідовну схему характеризують опорами її елементів R, Х, паралельну – відповідними провідностями G і В. Дві схеми заміщення одного двополюсника звичайно еквівалентні між собою, тому I=U/Z=UY, тобто Y=1/Z. Для послідовної схеми можна побудувати трикутник опорів (рис. 6.5.), для паралельної – трикутник провідностей (рис. 6.6). Оскільки в еквівалентних схемах кути j однакові,
Звідки випливають формули, які пов’язують параметри послідовної та паралельної схем заміщення:
Слід звернути увагу, що в схемах рис. 6.7 б,в в загальному випадку G≠1/R; B≠1/X. При аналізі результатів експерименту за законом Ома визначаються: Z=U/I, Y=I/U=1/Z (6.3) Величини R, X, G, В найпростіше визначити з трикутників опорів та провідностей.
а) б) в)
Рис. 6.7
Далі розглянемо питання про побудову топографічної або векторної потенціальної діаграми напруг, під якою розуміють векторну діаграму напруг електричного кола, на якій вектори напруг окремих елементів електричного кола розташовані у послідовності, що відповідає розташуванню самих елементів на ділянках електричного кола. При цьому вектор проведений з початку координат до будь-якої точки діаграми, визначає потенціал цієї точки в електричному колі. Вектори струмів на цій діаграмі розташовуються довільно і створюють векторну діаграму струмів. Доцільно зображати вектори струмів у тих точках, де є можливість перевірки суми струмів у вузлах на відповідність першому закону Кірхгофа. На рис.6.8 а зображена схема нерозгалуженого електричного кола і для неї побудована топографічна діаграма напруг (рис.6.8 б). Напрямок векторів напруг на цій діаграмі відповідає довільно обраному напрямку вектора струму І. Слід звернути увагу, що напрямки стрілок напруги відносно точок, між якими напруга розглядається, на схемі і топографічній діаграмі протилежні. Наприклад, напругу Uбв на схемі спрямовують від точки б до точки в. На діаграмі вектор
а) б)
Рис.6.8 Напруги на окремих елементах електричного кола визначаються за формулами:
Вектори напруг та струмів на топографічних діаграмах будуються у відповідних масштабах – Топографічна діаграма напруг дозволяє досить просто визначити напругу між будь-якими точками електричного кола: діюче значення й фаза напруги визначаються прямою, що з'єднує відповідні точки на цій діаграмі (наприклад напруга Uбг на рис.6.8 б).
Контрольні запитання: 1. Які величини використовують для характеристики синусоїдних струмів і напруг? 2. Від чого залежить кут зсуву між струмом і напругою на пасивній ділянці електричного кола? 3. Як залежить від частоти опір реактивних елементів? 4. Які співвідношення між активними, реактивними і повними опорами, а також між активними, реактивними і повними провідностями? 5. Для яких цілей використовуються і яким чином будуються векторні діаграми? 6. В чому полягає сутність символічного методу розрахунку електричних кіл синусоїдного струму? 7. Які переваги векторно-топографічних діаграм? 8. Яким фізичним процесам відповідають активна, реактивна і повна потужності? 9. Як складається баланс потужностей?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.114.94 (0.03 с.) |
 опори окремих споживачів і всього кола. Результати розрахунків занести в таблицю 6.4.
опори окремих споживачів і всього кола. Результати розрахунків занести в таблицю 6.4. провідності окремих споживачів і всього кола. Результати розрахунків занести в таблицю 6.5.
провідності окремих споживачів і всього кола. Результати розрахунків занести в таблицю 6.5.

 ;
;  ;
;  ;
; 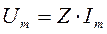 .
. ;
; 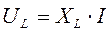 ;
;  ;
;  .
. ;
;  .
. .
. ;
; 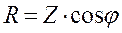 ;
;  ;
; 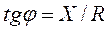 (6.1)
(6.1)
 - активну провідність (кондуктанс);
- активну провідність (кондуктанс); - індуктивну реактивну провідність (індуктивний
- індуктивну реактивну провідність (індуктивний - ємнісну реактивну провідність (ємнісний сусцептанс);
- ємнісну реактивну провідність (ємнісний сусцептанс); - реактивну провідність електричного кола (сусцептанс
- реактивну провідність електричного кола (сусцептанс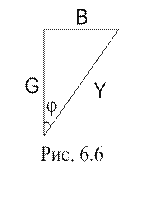
 ;
; 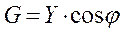 ;
;  ;
;  (6.2)
(6.2) ;
; 
 ;
;  ;
;  ;
;  .
.
 спрямований від точки в до точки б, що відповідає правилу віднімання векторів. Тому напрямок руху при побудові діаграми протилежний додатному напрямку струму і відповідає такій послідовності розташування елементів в електричному колі: С, R2, L, R1.
спрямований від точки в до точки б, що відповідає правилу віднімання векторів. Тому напрямок руху при побудові діаграми протилежний додатному напрямку струму і відповідає такій послідовності розташування елементів в електричному колі: С, R2, L, R1.
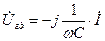 ;
;  ;
;  ;
; 
 ,
,