
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение размеренных цепей методом, обеспечивающим полную взаимозаменяемостьСтр 1 из 4Следующая ⇒
Таблица 7
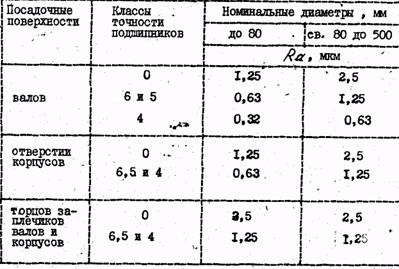
Шероховатость посадочных поверхностей валов и отверстий корпусов под подшипники качения не должны превышать величин, указанных в табл.8 Допускаемые отклонения от правильной геометрической форда посадочных поверхностей под подшипники качения 0 и 6 классов точности составляют 0,5 допуска на диаметр, а для 5 и 4-го классов - 0,25 допуска на диаметр. Допускаемые отклонения от перпендикулярности от посадочной поверхности к торцу могут быть выбраны по табл. 1.98 [7], принимая для подшипников 0 и 6 классов точности -7-8 степени точности, а для подшипников 5 и 4 классов точности - 6 и 5 степени точности. Таблица 8
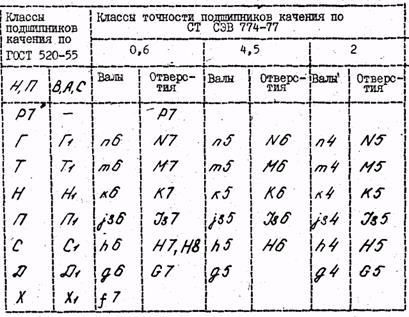
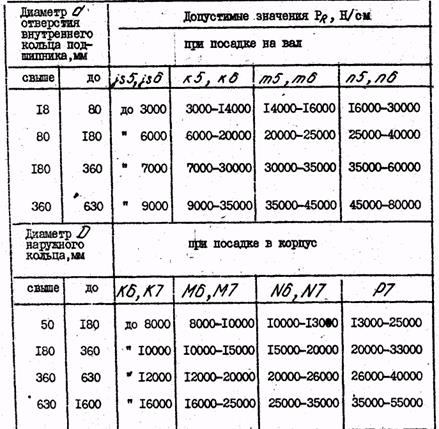
Характер сопряжения подшипника с валом в корпусом зависит от конструкции подшипника, величины, направления и характера нагрузок, действующих на него, а также от условий его эксплуатации и вида нагружения колец подшипника. Характер распределения контактных напряжений внутри подшипника различен для внутреннего и наружного колец, в связи с чем требуется и разливная их посадка на вал и корпус. Условия работы колец зависят так- же и от того, вращается или неподвижно данное кольцо относительно действующей на подшипник нагрузки. Различают три основных вида нагружения колец подшипника: местное, циркуляционное и колебательное, для осуществление соединении с натягом, позволяющие получить небольшую его величину. Используя для валов поля допусков n6, m6, k6, js6, или те же поля 5 и 4-го квалитетов. В табл. 7; даны поля допусков валов и отверстий под подшипники качения всех классов точности и приведено и соответствие посадкам, ранее применяемым по Г0СТ 520-55. Таблица 7
Шероховатость посадочных поверхностей валов и отверстий корпусов под подшипники качения не должны превышать величин, указанных в табл.8 Допускаемые отклонения от правильной геометрической форда посадочных поверхностей под подшипники качения 0 и 6 классов точности составляют 0,5 допуска на диаметр, а для 5 и 4-го классов - 0,25 допуска на диаметр. Допускаемые отклонения от перпендикулярности от посадочной поверхности к торцу могут быть выбраны по табл. 1.98 [7], принимая для подшипников 0 и 6 классов точности -7-8 степени точности, а для подшипников 5 и 4 классов точности - 6 и 5 степени точности.
Таблица 8
Характер сопряжения подшипника с валом в корпусом зависит от конструкции подшипника, величины, направления и характера нагрузок, действующих на него, а также от условий его эксплуатации и вида нагружения колец подшипника. Характер распределения контактных напряжений внутри подшипника различен для внутреннего и наружного колец, в связи с чем требуется и разливная их посадка на вал и корпус. Условия работы колец зависят так- же и от того, вращается или неподвижно данное кольцо относительно действующей на подшипник нагрузки. Различают три основных вида нагружения колец подшипника: местное, циркуляционное и колебательное.
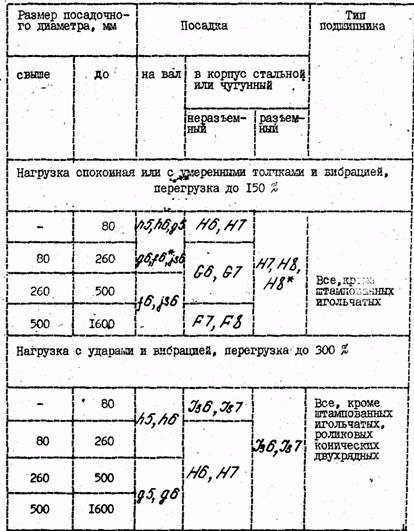
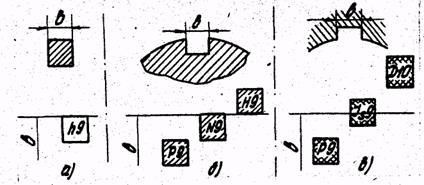
Рис. 9. Схемы нагружения колец подшипников качения Таблица 9 Рекомендуемые посадки для местно-нагруженных колец
* Применять при частоте вращения не более 0,6 nnp ( nnp - предельно допустимая частота вращения подшипников).
Таблица 10 Допустимые интенсивности радиальных нагрузок на посадочной поверхности вала и корпуса схемы нагружения которых представлена на рис. 9. Местное нагружение - кольцо воспринимает постоянную по направлению результирующую радиальную нагрузку Рn (например, силу тяжести конструкции, натяжение приводного ремня) лишь ограниченным участком окружности дорожки качения и передает ее соответствующему участку посадочной поверхности вала или корпуса. Это происходит тогда, когда кольцо подшипника не вращается относительно постоянно действующей нагрузки Pn(риc. 9 а, б) или когда кольцо вращается Кольцо, испытывающее местное нагружение, монтируется с зазором, который необходим для проворачивания его по посадочной поверхности, благодаря чему устраняется заклинивание тел качения, а износ беговой дорожки кольца происходит равномерно по всей окружности кольца. Посадки местно нагруженных колец подшипников могут быть выбраны [9] в соответствии с данными табл.9. циркуляционное нагружение - кольцо воспринимает результирующую постоянную по направлению радиальную нагрузку последовательно всей окружностью дорожки качения и передает ее также последовательно всей посадочной поверхности вала или корпуса. Это имеет место, когда кольцо подшипника вращается относительно постоянно действующей нагрузки Pn(рис. 9, а, б, в) или когда деталь, создающая нагрузку, вращается относительно неподвижного кольца (рис. 9, д, е, ж, з, и, к), а также, когда кольца вращаются с разными скоростями (рис. 9, г) при соблюдении указанных на рис. 9 условий.
Монтаж кольца, испытывающего циркуляционное нагружение, производят с натягом, а вид посадки выбирают по величине PR - интенсивности радиальной нагрузки на посадочной поверхности.
где R - радиальная реакция опоры на подшипник, Н; b - рабочая ширина посадочного места подшипника, см; b=B-2r; /B - ширина подшипника, r - радиус закругления/; K1 - динамический коэффициент посадки, зависящий от характера нагрузки (при перегрузке до 150 %, умеренных толчках и вибрации K1=1; при перегрузке до 300%, сильных ударах и вибрации K1=1.8); K2 - коэффициент, учитывающий степень ослабления посадочного натяга при полом вале или тонкостей ном корпусе (при сплошном вале Ка*I). Значения коэффициента К2 даны в табл. II; K3 - коэффициент неравномерности распределения радиальной нагрузки К. между рядами роликов в двухрядных роликоподшипниках или между сдвоенными шарикоподшипниками при наличии осевой нагрузки A на опору. Значения К3 в зависи-
Таблица 11 Значение коэффициента К2 мости от величины
(Угол Колебательное нагружение - невращающееся кольцо воспринимает действие равнодействующей Рр двух радиальных нагрузок (одна из которых Рn - постоянная по направлению, вторая — Pb, меньшая по величине, вращается) ограниченным участком окружности дорожки качения и передает ее соответствующему ограниченному участку посадочной поверхности вала или корпуса. Равнодействующая этих нагрузок Рp не совершает полного оборота, а колеблется между определенными точками (рис. 9; ж,з). В случае, если Pn < Pb, то кольца являются местно- или циркуляционно нагруженными в зависимости от схемы приложения сил (рис. д, и, к). Выбор посадок для колец, имеющих колебательное нагружение, следует производить согласно данным табл. 22, гл.6 [I].. Посадки колец радиально-упорных шарико- и роликоподшипников, перемещаемых при регулировании осевой игры, выбирают по табл.27, гл.6 [I]. При чисто осевой нагрузке вращающиеся внутренние кольца радиальных и радиально-упорных подшипников устанавливают на вал с посадками: h - при n < 0,6 nnp и is - при n>0.6nnp, где n и nnp - соответственно рабочая и предельная частота вращения подлинника, об/мин. Наружные кольца при этом устанавливают в корпус с зазором
Здесь l1, l2, l3... lk - действительдаеразмеры деталей;
действительных размеров деталей; ni - частота появления одного и того же размера, например, li; N - общее количество деталей в партии
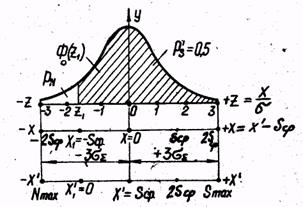
Рис. 10. Кривая нормального распределения и графическое изображение функции Ф0(Z) Кривая плотности вероятности нормального распределения симметрична относительно максимальной ординаты, а поле рассеивания случайной величины соответствует 2.1.Определение вероятного процента деталей в партии, имеющих погрешности, величины которых лежат в каком-либо заданном интервале. Ветви теоретической кривой нормального распределения, ухо-дят в бесконечность, асимпотически приближаясь к оси абсцисс. Площадь, ограниченная кривой и осью абсцисс, равна вероятности того, что случайная величина, например, погрешность размера, лежит в интервале от -
а так как кривая симметрична относительно максимальной ординаты, то
Для подсчета вероятности того, что погрешность находится в тех или иных пределах, пользуются табличным интегралом
значения которого приведены в таблице приложения [8]. Здесь случайная величина x выражена в долях от сигма и величина
Так как площадь, ограниченная кривой Гаусса и осью абсцисс, равна 1, а площадь, лежащая в пределах значении x =
можно утверждать, что случайная величина X не будет выходить за пределы -
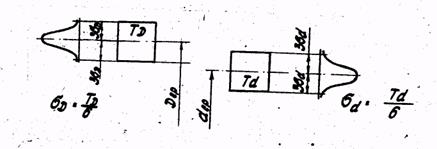
При этом вероятность выхода случайной величины за пределы значении В общем случае относительное количество деталей В% в партии, имеющих погрешность, выходящую за пределы X1 и Х2 (рис. 10), можно определить по формуле: B%=100-[Ф0(Z2)-Ф0(Z1)]100 ( 38) где Z1= 2.2. Определение вероятности получения зазоров и натягов в переходных посадках Рассмотренные выше положения могут быть использованы для определения наиболее вероятного количества сопряжений с зазором или натягом в переходных посадках при условии, что погрешности отверстий и валов случайны и подчиняются закону нормального распределения, а центр их группирования совпадает с серединой поля допуска, т.е. отсутствуют систематические погрешности и величина допуска Т каадой из сопрягаемых деталей соответствует 6 Тогда для переходной посадки, изготовленной в системе отверстия с полями допусков ТDи Tdсопрягаемых деталей, показанными на рис. 11, наиболее вероятный размер отверстия -Dср,вала - dcp, а среднее квадратическое отклонение размеров каждой из деталей, согласно выражению (37)
Рис. 11. Схема расположения полей допусков отверстия (TD) и вала (Td) в случае переходной -посадки Так как появление зазора или натяга в сопряжении является случайным явлением, которое зависит от размеров сопрягаемых валов и отверстии, а появление последних подчиняется закону нормального распределения, то получение зазора или натяга в соединении также подчиняется закону нормального распределения [8]. При этом среднее квадратичное отклонение суммарного распределения, согласно выражению (30), равно
Поскольку наиболее вероятным размером отверстия является-Dcp, а вала - d cp и Dcp>dc p , то наиболее вероятным соединением будет соединение с зазором Sср=Dcp-dcp, величина которого определяет положение центра группирования соединении с зазорами, относительно начала их отсчета (рис. 12), соответст-вующего точке Scp на оси х. На этой оси точка Х1=0 разделяет зазоры от натягов. Для большей наглядности проведем ось X, на которой отметим величины отклонении от центра группирования X=0. Координатой, разделяющей зазоры от натягов, будет Х1= = Scp. Относительно осей Zи Yстроят кривую нормального распределения зазоров и натягов в соединении используя таблицы значении (31), в которых случайная величина выражена через Z=x/
Рис. 12. Кривая нормального распределения зазоров и натягов, при Z1<O
где На рис. 13 изображена кривая распределения зазоров и натягов в соединении и даны соответствующие отметки на осях для случая, если в переходной посадке наиболее вероятным является натяг, тогда вероятность получения соединении с зазором PSи натягом PN Рис. 13. Кривая нормального распределения натягов и зазоров, когда Z1> О
где Наиболее вероятные предельные значения наибольших зазоров и натягов определяются величинами +- 3сигмаE. Фактическое их зна-чение для случая соединении с наиболее вероятным зазаром:
и для соединении с наиболее вероятным натягом:
Их величины обозначены на осях X (рис. 12 и I3). 3. Методы центрирования, точность и характер сопряжения шлицевого соединения с прямобочным профилем. Основными эксплуатационными требованиями и шлицевым соединениям являются передача расчетного крутящего момента и обеспечение центрирования втулки по валу. Шлицевые соединения предназначены как для подвижных (втулка перемещается вдоль вала), так и для неподвижных (втулка неподвижна относительно вала) посадок. Размеры шлицевнх прямобочных соединении регламентйрова- ны стандартом ГОСТ 1139-8О. Для обеспечения концентричности оси втулки относительно оси вала предусматривается центрирующая поверхность, которой могут быть: поверхность наружного диаметра D, поверхность внутреннего диаметра соединения d, а также боковая поверхность профиля зуба по размеру b(рис. 14).
Рис. 14 Способы центрирования втулки с валом для шлицевых соединении с прямобочным профилем Центрирование по Dприменяется, когда втулку термически не обрабатывают или когда твердость её материала после термообработки допускает калибровку протяжкой. Вал в этом случае шлифуется по размеру Dна круглошлифовальном станке. Этот способ центрирования прост, экономичен, его применяют для неподвижных соединении, так как в них отсутствует износ от осевых перемещений, а также для поднижные, воспринимающих небольшие нагрузки. Центрирование по dцелесообразно в том случае, когда втулка термически обработана и её твердость не допускает обработку чистовой протяжкой. Тогда d втулки шлифуют на внут-ришлифовальном станке, а d вала окончательно обрабатывают на шлицешлифовальном станке. Этот способ центрирования, являясь дорогим, обеспечивает, однако, точное центрирование поверхностей и применяется обычно для подвижных соединений. Центрирование по bиспользуется при передаче знакопеременных нагрузок, больших крутящих моментов, а также при реверсивном движении. Этот способ центрирования обеспечивает повышенную прочность соединения вследствие равномерного распределения нагрузки между зубьями, но не гарантирует точность центрирования и поэтому редко применяется. Посадки шлицевых соединении осуществляются в системе отверстия по центрирующей поверхности и по боковой поверхности впадин, т.е. по d и b или по D и b, или только по b. По нецентрирурующим диаметрам предусмотрены значительные гарантированные зазоры, которые в сочетании с предписанным стандартом гарантированным зазором по размеру b, обеспечивают собираемость пищевого соединения и компенсируют погрешности профиля и расположения шлицев вала и втулки. Допуски шлицевых соединениии с прямобочным профилем регламентированы стандартом. Отклонения размеров шлицевых отверстия и вала отсчитываются от соответствующих номинальных размеров D, d, b, которые взяты из ГОСТ 1139 -80. Стандарт ГОСТ 1139 -80 рекомендует посадки в зависимости от способа центрирования и выделяет из них предпочтительные. Поля допусков нецентрирующих диаметров должен соответствовать указанным в табл. 13, взятой из ГОСТ 1139-80. Таблица 13 Поля допусков нецентрирующих диаметров
* Диаметр dне менее диаметра d1по ГОСТ 1139 -80. При обозначении шлщевых соединении, их отверстий и валов указываются: поверхность центрирования (D, d, b), основные размеры соединения (ZxdxDxb) и посадки по каждому из размеров, помещенные после них. Примеры условных обозначении шлицевых соединении при центрировании по d, D и b, соответственно:
При этом обозначение шлицевого отверстия для всех случаев. соответственно:
и шлицевого вала:
При назначении посадки шлицевого соединения для практических целей можно пользоваться данными табл. 14. Таблица 14 3.1 Контроль точности пищевых деталей Для обеспечения собираемости шлицевых соединении необходимо, чтобы размеры параметров деталей соединения, отклонения формы и расположения шлицев находились в заданных пределах. Шлицевые детали в индивидуальным и мелкосерийном производ-ствах контролируют универсальными измерительными инструментами и приборами. В серийном в крупносерийном производствах шлицевые детали контролируют дифференцированно с помощью поэлементных гладких предельных калибров, которыми проверяют D, d и b, при этой для контроля параметров вала применяют скобы, а отверстия - пробки. Кроме того, вал проверяет комплексным шлицевым кольцом, а отверстие втулки - комплексной шлицевой пробкой, которые изготавливаются только проходными и являются прототипами сопрягаемых деталей: ими контролируют правильность взаимного расположения шлицев. Шлицевые валы и отверстия считаются годными, если размеры D, d и b находятся в установленных пределах, а комплекс- ный калибр соединяется с контролируемой деталью. Допуски на изготовление предельных поэлементных калибров определятся по стандартам на допуски предельных гладких калибров для контроля цилиндрических поверхностей в зависимос-ти от посадки контролируемого размера. Допуски и предельные отклонения на комплексные шлицевые калибры задаются стандартом и отсчитываются от соответствующих номинальных размеров. 4. ДОПУСКИ И ПОСАДКИ ШПОНОЧНЫХ СОЕДИНЕНИЙ. Шпоночные сопряжения применяются для соединения втулок, шкивов, зубчатых колес и муфт с валами при невысокой точности центрирования. Основным эксплуатационным требованием для них является - передача крутящего момента. Наибольшее распространение получили шпонки призматические, основные размеры которых регламентированы стандартом ГОСТ 23360-78 (СТ СЗВ 189-75). Стандарт не распространяется на шпоночные соединения, при-
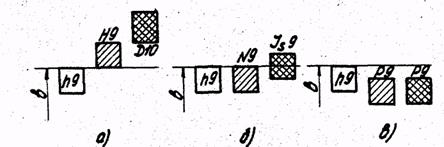
меняемые для крепления режущего инструмента. Для получения различных посадок призматических шпонок ГОСТ 2336-78 установил поля допусков на ширину b шпонок (рис. 15, а), пазов валов (рис. 15, б) и втулок (рис. 15, в).
Рис. 15. Поля допусков на ширину b шпонки (а), паза вала (б) и паза втулки (в) Стандартом установлены три типа шоночша соединений: свободное (рис. 16, а), которое используется для направляющие шпонок; нормальное (рис. 16, б); плотное (рис. 16, в), применяемое для неподвижных соединений. Рис. 16.- Размещение полей допусков на ширину b при свободном (а); нормальном (б) и плотном (в) шпоночном соединенииях. Стандартом нормированы отклонения высота шпонки по h11, глубины паза на валу t1 и паза во втулке t2, а также длины шпонок по h14 и длины пазов на валу по H15. 5. Cтепени и нормы точности зубчатых колес. Допуски цилиндрических эвольвентных зубчатых колес и передач внешнего и внутреннего зацеплений приводятся в ГОСТ 1643-81 [7], который соответствует рекомендации ИСО № 1328 "Точность цилиндрических зубчатых передач эвольвентного зацепления "и рекомендациям по стандартизации PC 3352-71; при модуле от 1 до 56 мм, делительном диаметре колес до 6300 мм, межосевом расстоянии до 6300 мм для прямозубых, косозубых и шевронных колес и передач. Указанный ГОСТ предусматривает 12 степеней точности зубчатых колес и передач, обозначенных в порядке убывания с 1-й по 12-ю. Для 1-й 2-й степеней точности отклонения в стандарте не даны. Приведенные отклонения относятся к окончательно изготовленным рубчатым колесам и передачам (точность заготовок колёс стандартом не нормируется). Для каждой степени точности установлены независимые допускаемые отклонения параметров зубчатых колес и передач, которые влияют на кинематическую точность колес и передач, на плавность их работы и на контакт зубьев передачи, в соответствии с чем стандарт предусматривает кинематическую норму точности, норму контакта зубьев и норну плавности работы. Независимо от степени точности зубчатых колес и передач стандарт устанавливает шесть видов сопряжений зубчатых колес (Н,Е, D, С, В, А), определящих величину бокового зазора jnmin) в передаче, а также восемь видов допусков на боковой зазор (h, d, с, b, a, z, у, x). В машиностроении наибольшее применение получили зубчатые колеса и передачи 7-9 степеней точности. В таблице 1.62 [7] да-ны рекомендации по выбору степеней точности зубчатых передач в зависимости от метода их нарезания, окончательной обработки рабочей поверхности, условий работы, окружной скорости и КПД. Размерная цепь состоит из замыкающего и нескольких составляющих звеньев. Размер, который получается последним в процессе обработки детали или сборки узла, называется замыкающим. Составляющими называются все звенья размерной цепи, с изменением величин которых изменяется замыкающее звено. Все составляющие звенья размерной цепи делится по отношению к замыкающему размеру на увеличивающие и уменьшающие в зависимости от того увеличивается или уменьшается замыкающий размер при увеличении каждого из составляющих размеров цепи. Основным условием для составления и анализа размерной цепи является ее замкнутость, однако, на чертежах размер замыкающего звена не проставляется, так как его размер и точность являются результатом обработки составляющих звеньев цепи. Для упрощения решения размерных задач размерные цепи часто изображают в виде размерных схем, в которых все составляющие звенья одной цепи обозначаются заглавной буквой русского алфавита с различными цифровыми индексами, например: А1, А2, А3, …, Аn, а замыкающее звено – аналогичной буквой с индексом
Рисунок 17. Пример двухзвенной размерной цепи. Расчет размерных цепей проводят для решения одной из следующих задач: 1) по заданным номинальным размерам и предельным отклонениям всех соответствующих звеньев нужно определить номинальный размер, допуск (предельные отклонения) замыкающего звена – проверочный расчет – первая задача; 2) по заданному допуску (предельным отклонениям) замыкающего звена необходимо найти рациональные значения допусков (предельных отклонений) составляющих звеньев – задача, решаемая при проектном расчете размерной цепи – вторая задача. Решение размерных цепей может производиться методом, обеспечивающим полную взаимозаменяемость (методом максимума - минимума), методом обеспечивающим неполную (ограниченную) взаимозаменяемость (теоретико-вероятностным методом), методом групповой взаимозаменяемости (селективной сборки), а так же методами пригонки и регулировки.
Первая задача
Базовая плоскость I детали (рисунке 18) обрабатывается вначале, затем от нее обрабатываются поверхности по размерам А1 и А2, имеющими допуски на изготовление соответственно ТА1 и ТА2. В технологической размерной цепи размер Аж является замыкающим поскольку его величина зависит от действительных размеров А1 (увеличивающего) и А2 (уменьшающего) звеньев. В данном случае номинальный размер и допуск замыкающего звена соответственно равны
В общем случае при m увеличивающих и n уменьшающих звеньях основные уравнения линейной размерной цепи можно представить в виде
Таким образом, допуск замыкающего звена в линейных размерных цепях равен сумме допусков всех (увеличивающих и уменьшающих) звеньев. Наибольший размер размыкающего звена рассматриваемой цепи
Что может быть представлено в следующем виде:
Вычитая из полученного выражения уравнение (45), получают расчетную зависимость для определения верхнего отклонения замыкающего звена данной цепи
Нижнее отклонение замыкающего звена по аналогии соответствует
В общем случае эти уравнения можно представить в виде
На основании уравнения (48) можно определить допуск любого составляющего звена при условии, что известны допуски и предельные отклонения остальных размеров цепи, включая и замыкающий, тогда
Это уравнение читается так: допуск любого составляющего размера размерной цепи равен допуску замыкающего размера минус сумма допусков остальных составляющих размеров цепи. Для определения предельных отклонений любого уменьшающего или увеличивающего размера следует пользоваться уравнениями (51, 52). При несимметричном расположении поля допуска относительно номинального размера в расчет вводится координата середины поля допуска Em (рисунок 19) и тогда для любого звена
По аналогии
Для решения указанных уравнений по зависимости (48) определяют допуск замыкающего звена
Рисунок 19. Схема к определению координаты середины поля допуска EmAi Для определения координаты середины поля допуска замыкающего звена следует использовать уравнение
При симметричном расположении поля допуска относительно номинального размера все величины Em будут равны нулю.
Вторая задача
Эта задача наиболее важна, так как её конечная цель - обеспечение точности функционального размера сборки, что может быть достигнуто лишь при правильном назначении допусков составляющих размеров. Эта задача может быть решена двумя способами, которые рассматриваются ниже. Способ назначения равных допусков применяют в случаях, если составляющие размеры являются величиной примерно одного порядка (например, лежат в одном интервале размеров системы допусков и посадок) и могут быть выполнены с одинаковой экономической точностью. Тогда условно принимают, что
и с учетом зависимости (48) средняя величина допуска размера
Этот допуск можно корректировать для отдельных составляющих размеров в зависимости от технологической трудности их изготовления, конструктивных особенностей в их величины, но при этом должно удовлетворяться уравнение (48). Способ назначения допусков одного квалитета точности применяют тогда, когда все составляющие цепь размеры могут быть изготовлены по какому-либо одному классу точности, и их допуски зависят от номинальных размеров звеньев цепи. Поскольку величина допуска каждого составляющего размера TAi= а i, где а число единиц допуска, характеризующее квалитет точности, а
Принимая по условию задачи а1 = а2 = … = … =аm, получим:
откуда среднее число единиц допуска
Здесь k = m + n, где m – число увеличивающих; а n – число уменьшающих звеньев По полученному значению am, которое в общем случае не будет равняться какой-либо из величин a, определяющих квалитет точности, назначают допуски на изготовление составляющих размеров по ближайшему квалитету. При этом допуски назначают исходя из конструкции деталей: для деталей типа "валов" - в минус, типа "отверстие" - в плюс, а для "ступенек" - в плюс-минус. После этого определяют величину Δ, на которую следует изменить один из составляющих размеров цепи, чтобы удовлетворялось равенство (48):
Здесь TAi' - допуски, назначенные по выбранному квалитету. Если Δ > 0, то на эту величину увеличивают допуск наиболее трудно обрабатываемого звена. Если Δ < 0, то на эту величину уменьшают допуск наиболее легко обрабатываемого звена. В случае, если замыкающий размер задается верхним и нижним отклонениями ( Первая задача
Как отмечалось в разделе 2.1., допуск размера принимается равным 6σ, в случае, если погрешности его изготовления подчиняются закону нормального распределения. Применительно к звеньям размерной цепи можно записать, что
Соответственно
На основании зависимостей (30) и (48) можно записать уравнение для определения допуска замыкающего звена тогда, когда центр группирования совпадает с серединой поля допуска, а диапазон рассеивания - с величиной допуска:
Когда центр группирования не совпадает с серединой поля допуска, а поле рассеивания - с величиной допуска, координата
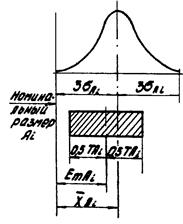
Рисунок 20. Смещение центра группирования эмпирической кривой распределения относительно номинального размера
где EmAi - координата середины поля допуска относительно номинального значения размера Ai α1 - коэффициент относительной асимметрии эмпирической кривой распределения отклонений i-го размера. Из формулы (64) следует, что
При симметричном расположении поля допуска относительно номинального размера EmAi = 0,
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.213.214 (0.164 с.) |
 1.5.2. Выбор посадок подшипников качения
1.5.2. Выбор посадок подшипников качения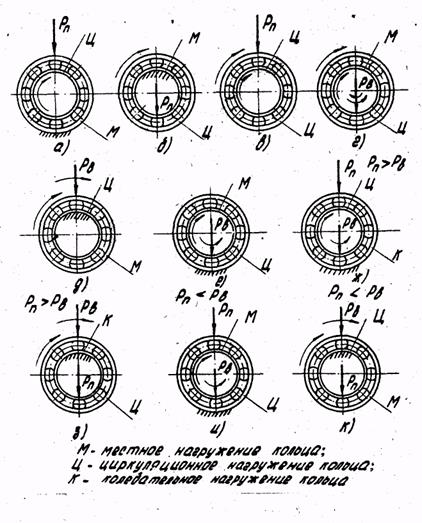
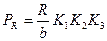 Н/см (29)
Н/см (29)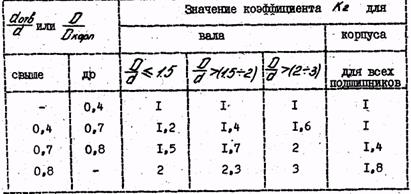
 [9], приведены в табл.12. Таблица 12
[9], приведены в табл.12. Таблица 12
 - угол контакта тел качения с дорожкой качения наружного кольца, он зависит от конструкции подшипника).Для радиальных и радиально-упорных подшипников с одним наружным или внутренним кольцом K3=1
- угол контакта тел качения с дорожкой качения наружного кольца, он зависит от конструкции подшипника).Для радиальных и радиально-упорных подшипников с одним наружным или внутренним кольцом K3=1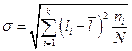 (32)
(32)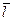 - среднее арифметическое значение
- среднее арифметическое значение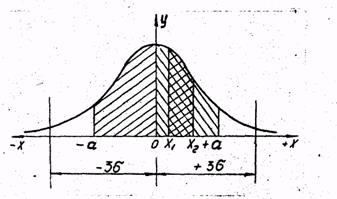
 Зб.
Зб.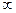 до +
до + 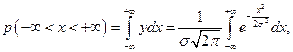 (33)
(33)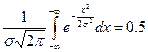
 (34)
(34)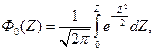 (35)
(35)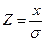 .Функция Ф0(Z), называется нормированной функцией Лапласа и соответствует площади, заключенной между кривой, осью симметрии и ординатой, соответствующей значению Z (рис. 10) и дает вероятность того, что величина погрешности находится в пределах от 0 до Z. Чтобы определить вероятность того, что погрешность x по своей абсолютной величине находится в пределах
.Функция Ф0(Z), называется нормированной функцией Лапласа и соответствует площади, заключенной между кривой, осью симметрии и ординатой, соответствующей значению Z (рис. 10) и дает вероятность того, что величина погрешности находится в пределах от 0 до Z. Чтобы определить вероятность того, что погрешность x по своей абсолютной величине находится в пределах  сигма и по таблице значении Ф0(Z) находят эту вероятность, соответствующую:
сигма и по таблице значении Ф0(Z) находят эту вероятность, соответствующую: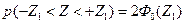 (36)
(36) . Поэтому при распределении случайной величины по закону Гаусса поле рассеивания R= 6
. Поэтому при распределении случайной величины по закону Гаусса поле рассеивания R= 6 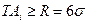 (37)
(37)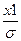 , Z2=
, Z2= 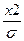 .
. (39)
(39)
 (40 )
(40 )
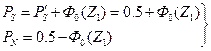 (41)
(41) и Z1<0;
и Z1<0; (4 2)
(4 2) и Z1>0.
и Z1>0. (43)
(43)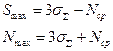 (44)
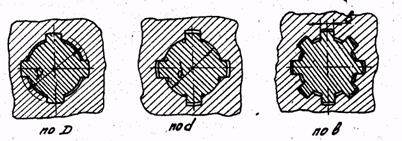
(44)

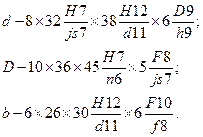

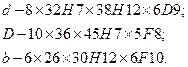
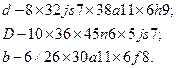
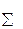 –
–  . На рис. 17 изображено соединение цилиндрических деталей с зазором, где зазор является замыкающим звеном, и дано схематическое изображение этой размерной цепи.
. На рис. 17 изображено соединение цилиндрических деталей с зазором, где зазор является замыкающим звеном, и дано схематическое изображение этой размерной цепи.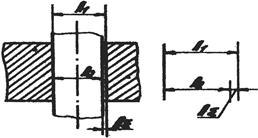
 (45)
(45)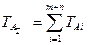 (46)
(46)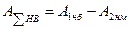
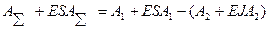
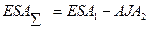 (49)
(49)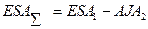 (50)
(50) (51)
(51) (52)
(52)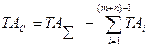 (53)
(53)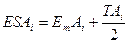 (54)
(54)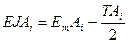 (55)
(55)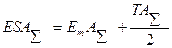 (56)
(56) (57)
(57)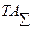 , который равен сумме допусков составляющих звеньев.
, который равен сумме допусков составляющих звеньев.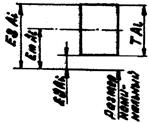
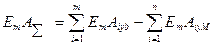 (58)
(58)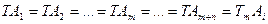
 (59)
(59)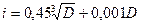 - единица допуска для интервала размеров от 1 до 500 мм, где D- средний размер интервала размеров по системе допусков и посадок, к которому относятся данный линейный размер, то уравнение (48) при наличии К звеньев можно записать в следующем виде:
- единица допуска для интервала размеров от 1 до 500 мм, где D- средний размер интервала размеров по системе допусков и посадок, к которому относятся данный линейный размер, то уравнение (48) при наличии К звеньев можно записать в следующем виде: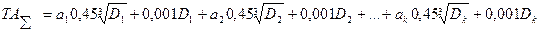
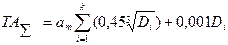
 (60)
(60)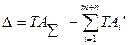
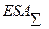 и
и  ), то после нахождения TA1, TA2, TA3 … (как было указано выше) определяются величины и знак верхних и нижних отклонений составляющих размеров так, чтобы они удовлетворяли уравнениям (51), (52).
), то после нахождения TA1, TA2, TA3 … (как было указано выше) определяются величины и знак верхних и нижних отклонений составляющих размеров так, чтобы они удовлетворяли уравнениям (51), (52).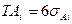 или
или 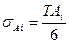 (62)
(62)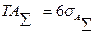 или
или 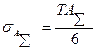
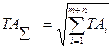 (63)
(63)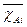 центра группирования (рисунок 20) эмпирической кривой распределения относительно номинального размера будет
центра группирования (рисунок 20) эмпирической кривой распределения относительно номинального размера будет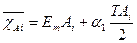 (64)
(64)
 (65)
(65)


