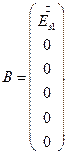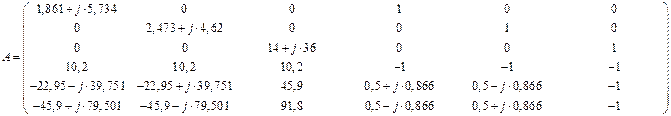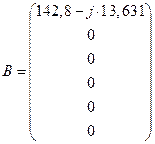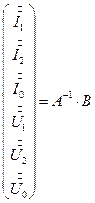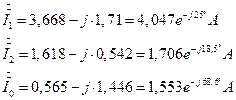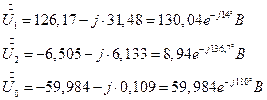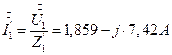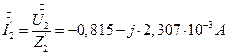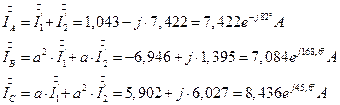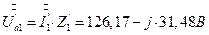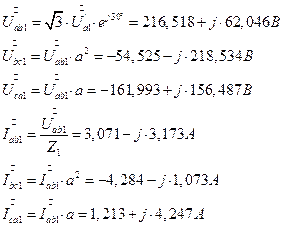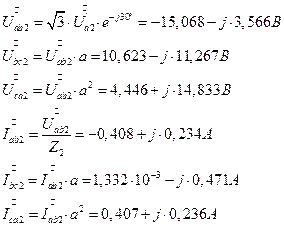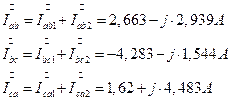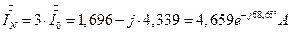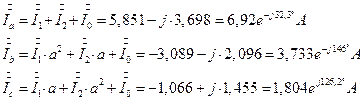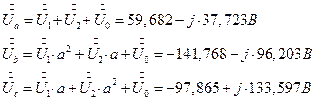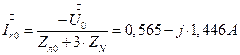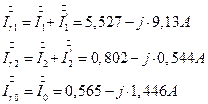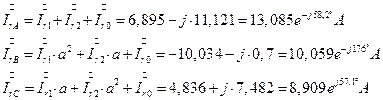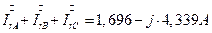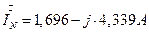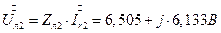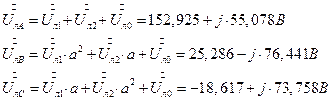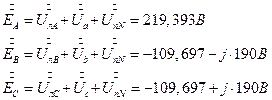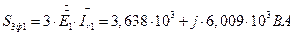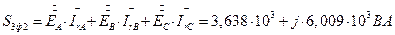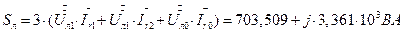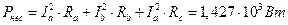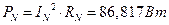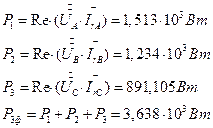Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет методом симметричных составляющих несимметричного режима в трехфазной цепи ⇐ ПредыдущаяСтр 3 из 3
Программа задания
1. Методом симметричных составляющих рассчитать заданный несимметричный режим в трехфазной цепи. Исходные данные для расчета цепи берем из п. 1 задания №3. Примечание. Если фазные сопротивления имеют вид 2. Указания по изменению схемы цепи и расчету ее параметров: отключить первый приемник; к зажимам а, b, с подключить соединенный в звезду, несимметричный, чи- сто активный приемник:
3.Значения коэффициентов 4. сопротивления фаз линии составляющим токов прямой и обратной последовательней одинаковы и равны 5. сопротивления фаз симметричного приемника составляющим токов прямой обратной и нулевой последовательней следует определить по формулам:
6. действующие значения фазных ЭДС те же, что и в п. 1. Для студентов, желающих выполнить вариант задания повышенной трудности, фазные ЭДС могут быть определены по формулам:
Значения коэффициентов
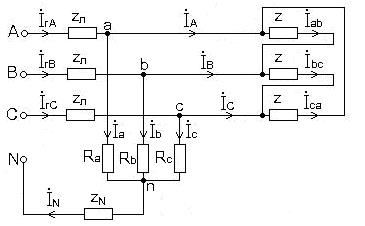
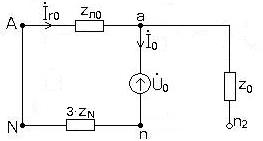
Пример расчета несимметричной трехфазной цепи методом симметричных составляющих 7.1. Схема цепи приведена на рис. 1. 7.1.1. Параметры нагрузок и источника питания 7.1.1.2. Параметры несимметричного приемника. Значения коэффициентов:
Сопротивления нейтрали 7.1.1.3. Сопротивления фаз линии составляющим токам прямой, обратной и нулевой последовательностей:
7.1.1.4. Сопротивления симметричного приемника составляющим токам прямой, обратной и нулевой последовательностей:
Рис. 1
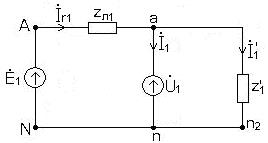
Рис.2
Рис. 3 Рис. 4
Рис. 5 Рис. 6
Рис. 7 Рис. 8
7.1.1.4. Параметры трехфазного источника питания. Значения коэффициента.
7.2. Расчет токов и напряжений во всех фазах трехфазной цепи. 7.2.1. Разложим заданную систему фазных ЭДС на симметричные составляющие. В данном примере система фазных ЭДСсимметрична и не содержит составляющих обратной и нулевой последовательности. 7.2.2. Преобразуем треугольник в звезду. Схема цепи изображена на рис. 2.
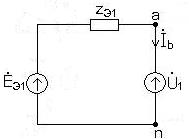
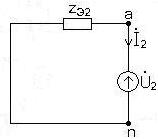
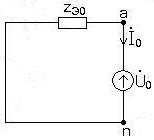
Схемы однофазных цепей для определения симметричных составляющих токов и напряжений прямой, обратной и нулевой последовательности приведены на рис. 3, 4,5. 7.2.3. Уравнения, представляющие фазные напряжения и токи несимметричного приемника через симметричные составляющие.
7.2.4. Расчет параметров преобразованных схем цепей для определения симметричных составляющих токов и напряжений прямой, обратной и нулевой последовательностей.
7.2.5. Схемы преобразованных цепей для определения симметричных составляющих токов и напряжений прямой, обратной и нулевой последовательностей рис. 6, 7, 8. 7.2.6. Система уравнений для определения симметричных составляющих токов и напряжений несимметричного приемника.
Шесть уравнений - шесть неизвестных. Первые три уравнения - основные уравнения. Контурные Кирхгофа для схем цепей рис. 6, 7,8. Дополнительные три уравнения - закон Ома для фаз несимметричного приемника, где соответствующие напряжения и токи разложены на симметричные составляющие по формулам (1). Система уравнений (2) представлена ниже в матричной форме:
Введем обозначения:
Численные значения матриц:
7.2.7. Решение системы уравнений.
7.2.8. Симметричные составляющие токов несимметричного приемника.
7.2.8. 1. Симметричные составляющие напряжений несимметричного приемника.
7.2.9. Определение симметричных составляющих токов симметричного приемника. Схемы рис. 6, 7, 8.
7.2.10. Определение линейных токов симметричного приемника через симметричные составляющие токов симметричного приемника.
7.2.11. Симметричные составляющие фазных напряжений на симметричном приемнике (звезде) рис. 2. Определение через симметричные составляющие токов и соответствующие сопротивления.
7.2.12. Симметричные составляющие напряжений и токов симметричного приемника (треугольник) прямой последовательности.
7.2.13. Симметричные составляющие напряжений и токов симметричного приемника (треугольник) обратной последовательности.
7.2. 14. Фазные напряжения на симметричном приемнике (треугольнике), определенные через симметричные составляющие фазных напряжений.
7.2. 14.1. Фазные токи симметричного приемника (треугольника).
7.2. 14.2. Проверка токов по узловому уравнению Кирхгофа: узлы a, b,c.
7.2. 15. Определение тока нейтрали несимметричного приемника.
7.2. 15.1. Определение смещения нейтрали.
7.2. 16. Определение токов несимметричного приемника через симметричные составляющие токов несимметричного приемника.
7.2. 17. Определение фазных напряжений несимметричного приемника через токи и сопротивления несимметричного приемника по закону Ома.
7.2. 17.1. Определение фазных напряжений несимметричного приемника через симметричные составляющие напряжений. Второй способ.
7.2. 18. Определение симметричных составляющих токов через генератор. Схемы рис. 11, 12, 13. 7.2. 18.1. Первый способ. Используем контурное уравнение Кирхгофа.
7.2. 18.2. Второй способ. Через симметричные составляющие токов приемников. Узловые уравнения Кирхгофа.
7.2. 19. Определение фазных токов (через генератор) через симметричные составляющие токов генератора.
7.2. 19.1. Проверка результатов расчета в цепи по узловому уравнению Кирхгофа для узла N.
7.20. Определение симметричных составляющих напряжений на сопротивлениях линии. Схемы рис. 6,7, 8.
7.20.1. Определение напряжений на сопротивлениях линии через симметричные составляющие.
7.20.2. Проверка результатов расчета напряжений на фазах трехфазной цепи по контурному уравнению Кирхгофа. Вычисление значений фазных ЭДС источника.
Заново определили систему заданных фазных ЭДС. Совпало с исходными данными. 7.3. Вычисление комплексных значений полных мощностей линии, приемников и трехфазного источника двумя способами. Проверка выполнения баланса мощностей. 7.3.1. Определение мощности трехфазного источника двумя способами. 7.3.1.1. Первый способ. Используем формулы для мощности метода симметричных составляющих.
Источник симметричен, отсутствуют ЭДС обратной и нулевой последовательности. 7.3.1.2. Второй способ. Используем формулы для мощности комплексного метода. Через ЭДС и токи генератора.
7.3.2. Определение мощности приемников. 7.3.2. 1. Линия. 7.3.2. 1.1. Первый способ. Используем формулы для мощности метода симметричных составляющих.
7.3.2. 1.2. Второй способ. Используем формулу для активной мощности.
7.3.2. 2. Несимметричный приемник.
7.3.2. 3. Симметричный приемник. 7.3.2. 3.1. Первый способ. Используем формулы для мощности метода симметричных составляющих.
7.3.2. 3.2. Второй способ. Используем формулы для мощности комплексного метода. Через напряжения и фазные токи.
7.3.2. 3.3. Третий способ. Используем формулу для активной мощности.
7.3.2. 4. Мощность, рассеиваемая в нейтрали.
7.3.2. 5. Комплекс полной мощности приемников.
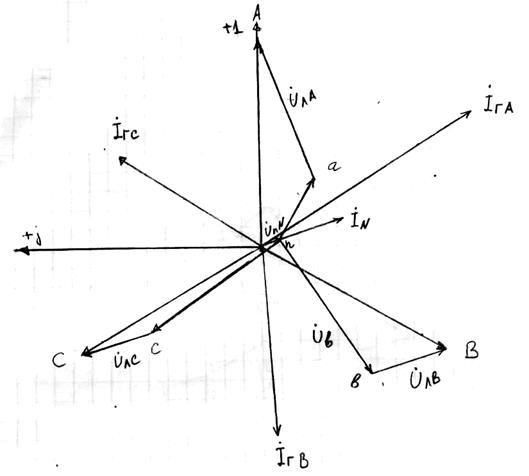
Баланс мощностей выполняется. 7.4. Расчет и построение топографической диаграммы напряжений, совмещенной с векторной диаграммой токов. 7.4.1. Определение потенциалов точек a, b, c для построения топографической диаграммы.
Топографическая диаграмма представлена на рис. 9.
Рис.9
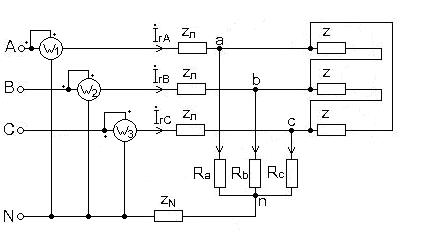
7.5. Выбор схемы измерения активной мощности в несимметричной трехфазной цепи. Вычисление активной мощности. В схеме имеется нейтральный провод, поэтому выбираем схему трех ваттметров, рис. 10.
Совпало с определенной в п. 3.3. активной мощностью.
Рис. 10
Литература 1. Демирчян К.С. и др. Теоретические основы электротехники. 4-е изд. – СПб.: Питер. 2003. – Т.1. 424с. 2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи: учеб. для вузов/ 11-е изд., исп. и доп. – М.: Гардарики. 2006. – 701с. 3. Бессонов Л.А. Сборник задач по теоретическим основам электротехники: Учеб. пособие – 4-е изд., перераб. и исп. – М.: Высш. Шк., 2003. – 528с.
Учебно-методическое издание
|
|||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 771; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.190.167 (0.068 с.) |
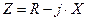 , то их следует заменить на
, то их следует заменить на 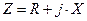 .
. ,
,  ,
,  .
. задаются преподавателем. В цепях, где нет нейтрального провода (схемы 1,3,4,6) следует его организовать и к нему подключить нейтраль несимметричного приемника. В нейтральный провод следует ввести
задаются преподавателем. В цепях, где нет нейтрального провода (схемы 1,3,4,6) следует его организовать и к нему подключить нейтраль несимметричного приемника. В нейтральный провод следует ввести  .
. . Для тока нулевой последовательности
. Для тока нулевой последовательности  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. задаются преподавателем.
задаются преподавателем.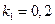 ,
, 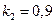 ,
,  .
. ,
, 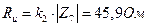 ,
, 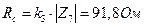 .
.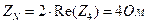 .
.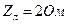 ,
, 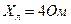 .
.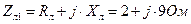 ,
, 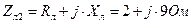 ,
, 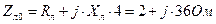 .
.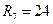 ,
, 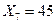 .
.




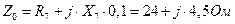
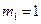 ,
, 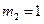 ,
, 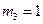 .
. ,
, 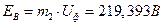 ,
, 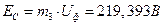 .
.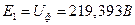 ,
,  ,
, 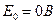 .
.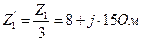 ,
,  ,
,  .
.
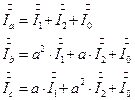 (1)
(1)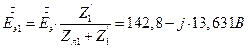
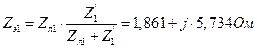


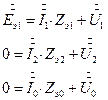
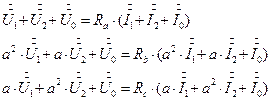 (2)
(2)