
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет статически неопределимой стержневой системы, содержащей абсолютно жесткий элемент ⇐ ПредыдущаяСтр 2 из 2
Методические указания по выполнению расчетно-графической работы для студентов специальностей 2903, 2906,2907, 2908, 2910 Казань, 2006 г. Составитель: Р.А.Каюмов УДК 539.3 Расчет статически неопределимой стержневой системы, содержащей абсолютно жесткий элемент; Методические указания по выполнению расчетно-графической работы для студентов специальностей 2903, 2906, 2907, 2908, 2910 / КазГАСУ; сост. Р.А. Каюмов. Казань, 2005, 24 с. В данных методических указаниях кратко излагается методика расчета простейших ферменных конструкций с жестким элементом и приводится пример расчета. Илл.6. Рецензент канд.физ.-мат. наук, проф. Кафедры теоретической механики КГАСУ Шигабутдинов Ф.Г. ã Казанский государственный архитектурно-строительный университет ЗАДАНИЕ № 3 РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ ШАРНИРНО-стержневой системы Для заданной шарнирно-стержневой системы (см.схему), состоящей из абсолютно жесткого бруса и упругих стержней с заданными соотношениями площадей поперечных сечений, требуется: 1. Установить степень статической неопределимости. 2. Найти усилия в стержнях. 3. Записать условия прочности для стержней от силовых воздействий и произвести подбор поперечных сечений стержней с учетом заданных соотношений площадей. Материал Ст-3, предел текучести принять равным 240 МПа = 24 кН/см2, коэффициент запаса прочности k = 1,5. 4. Найти напряжения в стержнях от неточности изготовления стержней d 1 = d 2 = d 3 = 5. Найти напряжения в стержнях от изменения температуры в стержнях на Dt° (см. табл.3). Коэффициент линейного расширения для стали 6. Сделать проверку прочности системы при различных вариантах силовых и несиловых воздействий: 1) конструкция собрана, еще не нагружена, но произошел перепад температур; 2) случай, когда нет перепада температур, а конструкция собрана и нагружена. 3) случай, когда конструкция собрана, нагружена и произошел перепад температур. 7. Определить предельную грузоподъемность системы и истинный коэффициент запаса прочности, приняв постоянное соотношение между Задание выполняется в полном объеме студентами специальностей ПГС и АД. Студенты других специальностей выполняют расчет системы только на внешнее нагружение по допускаемым напряжениям и по допускаемой нагрузке, исключив стержень 3.
Исходные данные для выполнения расчетно-графической работы выбираются по шифру, выдаваемому преподавателем.
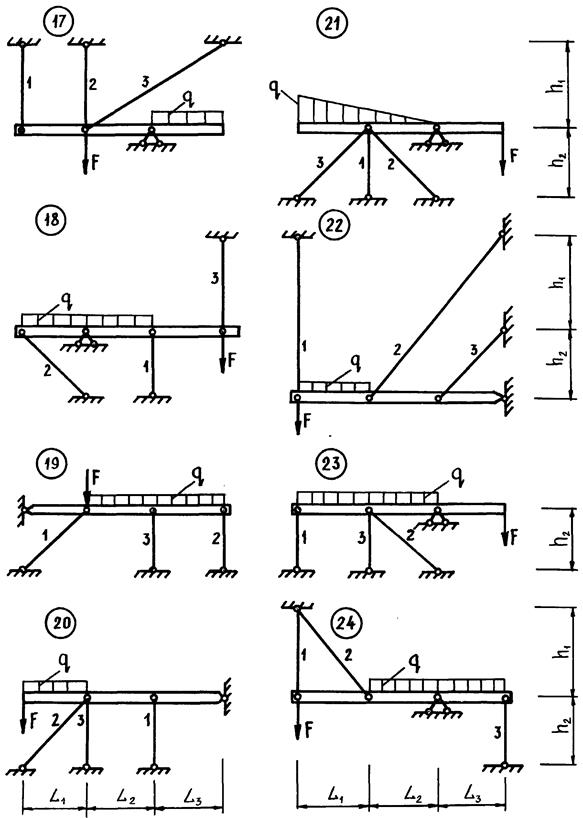
Схемы к заданию № 3
таблица 3
ПОСТАНОВКА ЗАДАЧИ Рассматривается шарнирно-стержневая система (рис.1), состоящая из жесткого бруса и деформируемых стержней, изготовленных с заданным соотношением площадей поперечных сечений, которое указывается в задании. Известны проектные нагрузки F, q; размеры конструкции h 1, h 2, L 1, L 2, L 3; проектные колебания температуры: D t 1 - в первом стержне, D t 2 - во втором, D t 3 - в третьем; неточности изготовления стержней, а именно d 1 – отличие от проектной длины в первом стержне, d 2 – во втором, d 3 – в третьем. Известны механические характеристики материала: модуль упругости Е = 2×104 кн/см2, предел текучести sт = 24 кн/см2, коэффициент температурного расширения a =125×10-71/Град. Коэффициент запаса прочности k для этой конструкции принимается равным 1,5.
Рис.1 Необходимо решить 3 задачи: 1. Произвести подбор сечений стержней для изготовления этой системы из условия прочности этих стержней по допустимым напряжениям при проектных нагрузках. 2. Сделать заключение о допустимости проектных колебаний температуры и неточностей изготовления стержней. 3. Найти предельную грузоподъемность конструкции, допустимые нагрузки и истинный запас прочности. Таким образом, работа состоит из проектировочного расчета, поверочного расчета, расчета предельных нагрузок для системы.
В РГР должны быть приведены 3 рисунка (выполненных в масштабе): исходная схема стержневой системы, силовая схема и кинематическая схема деформирования конструкции. Перед выполнением РГР рекомендуется изучить тему "Растяжение-сжатие" и уяснить следующие понятия и положения. 1. Напряжение, деформация, перемещение, продольная сила (нормальная сила). 2. Метод сечений. 3. Закон Гука. 4. Удлинение от изменения температуры. 5. Предел прочности, допустимое напряжение, условие прочности. 6. Пластическое течение, предел текучести. 7. Статическая неопределимость. 8. Условие совместности деформаций. 9. Расчет по допускаемым напряжениям. 10. Расчет по теории предельного равновесия.
ОБЩИЙ ПЛАН РАСЧЕТА КОНСТРУКЦИИ
Вначале конструкцию освобождают от связей, заменяя их реакциями. Методом сечений вводят в рассмотрение внутренние продольные силы (нормальные силы), возникающие в стержнях. При этом направлять их нужно от сечения, т.е. условно считать стержни растянутыми. Определить реакции и продольные силы из уравнений равновесия не удается, т.к. в плоской задаче статики можно составить 3 независимых уравнения равновесия, число же неизвестных силовых факторов (реакций и продольных сил) больше трех. Поэтому необходимо составить дополнительные уравнения, вытекающие из предположения о деформируемости стержней (уравнения совместности деформаций, связывающие удлинения стержней между собой). Вытекают они из геометрических соображений. При этом используется предположение о малости деформаций. Кроме того, необходимо учесть следующее правило знаков. Полную разницу между проектной длиной стержня l и конечной истинной длиной l кон обозначают через D l. Следовательно, если стержень удлиняется, то Как видно из рис.2, изменение длины стержня D l складывается из удлинения D l ( N ), вызванного усилием осевого растяжения N, удлинения D l (t), вызванного изменением температуры, и неточности изготовления d.

Рис.2 Если температура понижается, то D t < 0, то длина стержня уменьшается, т.е.
Поскольку удлинения выражаются через продольные силы В рассматриваемой РГР не требуется отыскивать реакции. Поэтому из 3-х уравнений равновесия достаточно оставить одно – условие равенства нулю моментов всех внешних и внутренних сил относительно оси, проходящей через центр шарнира D (рис.1). Решение полученной системы (уравнений равновесия и совместности деформаций) позволяет отыскать усилия Далее проводятся проектировочный (задача 1) и поверочный (задача 2) расчеты методом допустимых напряжений. За опасное напряжение принимается предел текучести sт. Согласно метода допустимых напряжений конструкция считается вышедшей из строя, если напряжение достигло опасного значения хотя бы в одном стержне, т.е. оказался разрушенным хотя бы один из стержней:
Для обеспечения безопасности конструкции требуется наличие запаса прочности, т.е. должно выполняться условие прочности вида
где k - коэффициент запаса, [ s ] - допустимое напряжение. Далее решается задача 3. Разрушение одного элемента конструкции не всегда означает потерю ее эксплуатационных свойств (т.е. обрушения). Другие элементы могут взять на себя нагрузку или ее часть, которую должен был нести разрушенный элемент. Это соображение используется в задаче 3, решаемой методом предельного равновесия, называемого еще методом допустимых нагрузок. В постановке задачи предполагается, что силы Р и Q увеличиваются пропорционально (Р / Q = const), площади сечений стержней известны из решения задачи 1, материал стержней - упруго-идеально-пластический. При увеличении нагрузки сначала "потечет" один стержень, напряжение в нем при дальнейшей деформации не будет увеличиваться и по модулю останется равным пределу текучести sт (см.рис.3). Последующее увеличение нагрузок приведет к тому, что сначала во втором, а затем и в третьем стержнях начнется пластическое течение, т.е. напряжения достигнут предела текучести. Очевидно, что какими бы ни были в начале процесса монтажные или температурные напряжения, наконец наступает момент, когда во всех стержнях напряжения достигнут предела текучести (т.к. они не могут принять больших значений, согласно диаграмме деформирования на рис.3). Достигнутые значения сил F = F пр и Q = Q пр называются предельными, т.к. их увеличение невозможно, а система начнет неограниченно деформироваться. Поскольку усилия Ni в предельном состоянии известны (т.к. выражаются через напряжения), то из уравнения равновесия определяется F пр. Из условия безопасности нагружения находятся допустимые нагрузки
Рис.3
Как видно из рассуждений при решении задачи 3, наличие изменений температуры или неточностей изготовления стержней не уменьшает грузоподъемности конструкции, если стержни изготовлены из упруго-идеально-пластического материала.
ПРИМЕЧАНИЯ
1. Преподаватель может конкретизировать задачу подбора стержней, потребовав использовать сортамент прокатной стали, например, подобрать составное сечение из уголков по таблицам сортамента (см. пример расчета). 2. При вычислениях достаточно оставлять 3 значащие цифры.
3. При подборе размеров стержней допускается 5 % перегрузки. Пример расчета Пусть дана шарнирно-стержневая система (рис.4). Известно, что E = 2×104 кн/см2, s т = 24 кн/см2, a = 125×10-7 1/град. (5)
Требуется подобрать уголок для изготовления стержней, причем первый должен быть изготовлен из двух уголков, а второй – из пяти, тогда A 1 / A 2 = 2/5. Сначала выпишем соотношения, которые являются общими для задач 1 и 2. 1. Определим необходимые геометрические параметры системы:
sin a1 = MC/BM = 0,8 sin a2 = DK/CK = 0,6 (8) 2. Введем осевые усилия методом сечений (по правилу знаков они направляются от сечения) и рассмотрим силовую схему конструкции (рис.5). Определим степень статической неопределимости системы, которая равна числу неизвестных усилий n плюс число оставшихся реакций r минус число независимых уравнений равновесия (три): m= n + r -3. В нашем случае 3. Составим одно уравнение равновесия Равенство нулю суммы моментов относительно оси, проходящей через опору D, дает:
где b1 = (L 1 + L 2) sina1 = 5,6 м, b 2 = L 2 sina2 = 2,4 м, Q = q × L 3 = 160 кн. (10) Или: -
Рис.5 4. Составим уравнение совместности деформаций. Оно нужно для решения задач 1,2. Кинематическая схема деформирования системы приведена на рис.6. При составлении уравнения совместности деформаций используем то, что деформации малы. Тогда можно считать, что ВВ¢ ^ BD, B¢B² ^ BB² и т.д. Из рис.6 видно, что
Рис.6
Здесь учтено, что первый стержень укорачивается, следовательно
C другой стороны
Отсюда
Подставляя
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 2042; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.192.3 (0.044 с.) |
 (см. табл.3). Если
(см. табл.3). Если  1/град.
1/град. и
и  .
.


 , кН
, кН
 , кН/м
, кН/м
 , м
, м
 , м
, м
 , м
, м
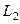 , м
, м
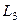 , м
, м
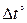
 , мм
, мм



 , если укорачивается, то
, если укорачивается, то 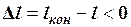 .
.
 ; если стержень сделан короче проектного, то d < 0. С учетом закона Гука это соотношение примет вид:
; если стержень сделан короче проектного, то d < 0. С учетом закона Гука это соотношение примет вид: . (1)
. (1) по формулам (1), то из уравнений совместности вытекают соотношения, связывающие между собой искомые усилия. Здесь и далее для упрощения записи используются следующие обозначения:
по формулам (1), то из уравнений совместности вытекают соотношения, связывающие между собой искомые усилия. Здесь и далее для упрощения записи используются следующие обозначения:  продольная сила и напряжение в стержне с номером i.
продольная сила и напряжение в стержне с номером i. . (2)
. (2) , (3)
, (3)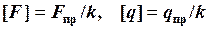

 ,
,  , d1 = - 3 мм, d2 = -1 мм. (6)
, d1 = - 3 мм, d2 = -1 мм. (6)
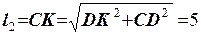 м (7)
м (7)
 (9)
(9) кн×м (11)
кн×м (11) Рис.4
Рис.4
 . (12)
. (12)
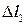 < 0. Чтобы связать
< 0. Чтобы связать 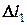 и
и  используется подобие треугольников DBB ¢ D и DCC ¢ D:
используется подобие треугольников DBB ¢ D и DCC ¢ D: (13)
(13) и
и 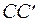 выражаются через удлинения стержней
выражаются через удлинения стержней  ,
, 

 и
и  в (13) получим уравнение совместности деформаций:
в (13) получим уравнение совместности деформаций: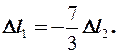 (14)
(14)


