
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зв’язок між розв’язком неоднорідної і відповідної однорідної системи рівнянь.
Нехай задано неоднорідну систему
Означення. Відповідною однорідною системою називається система
з тими ж самими коефіцієнтами Звя’язок між розв’язками системи (1) та (2) описується наступними теоремами. Теорема 1. Сума розв’язків неоднорідної і відповідної однорідної системи лінійних алгебраїчних рівнянь є розв’язком неоднорідної системи. Теорема 2. Різниця двох розв’язків неоднорідної системи є розв’язком відповідної однорідної системи. Доведення теореми 1. Нехай ( За означенням розв’язку маємо систему правильних числових рівностей
Підставимо в ліву частину системи (1) замість
Перша властивість доведена.
Доведення теореми 2. Нехай ( За означенням розв’язку маємо системи правильних числових рівностей:
Підставимо в ліву частину рівнянь системи (2) замість
Таким чином, одержуємо Твердження. З цих двох теорем випливає такий алгоритм розв’язування неоднорідної системи рівнянь: множину всіх розв’язків можна одержати додавання до кожного розв’язку множини розв’язків однорідної системи одного розв’язку (окремого) неоднорідної системи. Доведенння твердження. Нехай Н=
Нехай Розглянемо суму
Виникає питання, може система (1) має інші розв’язки, що отримуються за іншим алгоритмом? Доведемо, що цього не може бути. 2) Нехай Алгебра матриць
Розглянемо спочатку квадратні матриці одного і того ж n- го порядку. Для матриць введено три операції: 1) множиння матриць; 2) додавання матриць; 3) множиння матриці на число. Множиння матриць. Означення. Добутком матриць А і В називається матриця С того ж самого порядку, що матриці А та В, елементи якої утворюються за таким законом:
елемент А=
Закони множення. 1. Множення матриць, взагалі кажучі, не комутативне. Для того, щоб в цьому переконатись,досить знайти дві матриці А і В, для яких А×В ¹ В×А. А= А×В =
В×А = З наведеного прикладу бачимо, що А×В ¹ В×А. При цьому ми виходили з такого означення рівних матриць. Означення. Матриці А і В називаються рівними, якщо на одних і тих самих місцях знаходяться рівні елементи. Теорема. Множення матриць підпорядковується асоціативному закону. Тобто ми повинні довести, що для будь-яких матриць А, В і С має місце рівність (А × В) × С = А × (В × С). Нехай А=(
(А × В) × С = C ×D = F ( А × (В × С) = А× Р = Т ( В цих позначеннях треба довести, що F = Т, тобто Обчислимо
Підставимо (2) в (1), отримаємо
Преходимо до обчислення
Підставимо (5) в (4), отримаємо
Порівнюючи (3) і (6), приходимо до висавку, що Хоча множення матриць, взагалі кажучі, некомутативне, існує матриця, яка комутує з будь-якою матрицею А, і більш того, в добутку з даною матрицею не змінює цю матрицю А. Це так звана одинична матриця: Е = Ця матриця має такі властивості: 1) А × Е = А, " А 2) Е × А = А, " А, а звідси випливає, що А × Е = Е × А. Доведемо другу властивість.
Е × А =
=
Так само доводиться перша властивість, тобто безпосереднім множенням. Теорема. Доведеня. Нехай задано матриці А і В, а С – добуток цих матриць. Треба довести, що det C = det A ×det B. Для доведення побудуємо визначник d порядку 2n:
d =
Застосуємо до перших n рядків цього визначника теорему Лапласа d = det A ×det B ( d = det A ×det B (1) Перетворимо визначник d за допомогою восьмої властивості визначників. До (n+1) стовпчика додамо перший стовпець помножений на
Аналогічно зробимо з (n+2)-им стовпцем, (2n)-им стовпцем. В правому нижньому куті отримаємо нульовий блок порядку n. А правий верхній кут, тоді перетворюється в елементи матриці С.
Застосуємо до цього визначника теорему Лапласа. d = det C Користуючись формулою суми 2n членів арифметичної прогресії, маємо d = det C Вправа. Довести самостійно єдиність одиничної матриці (скористатись методикою доведення єдиності нульового вектора будь-якого лінійного простору).
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 376; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.30.253 (0.021 с.) |
 ,
,  (1)
(1) ,
,  (2)
(2) .
. ) – розв’язок системи (1), (
) – розв’язок системи (1), (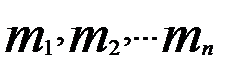 ) – розв’язок системи (2). Треба довести, що
) – розв’язок системи (2). Треба довести, що 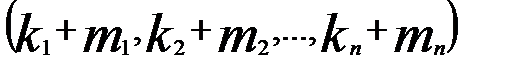 - розв’язок системи (1).
- розв’язок системи (1).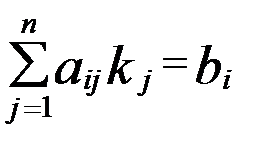 , (
, (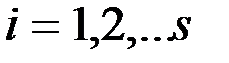 ) (3)
) (3) , (
, ( ) (4)
) (4)
 .
.
 (
( )
) ), (
), ( ) – розв’язки системи (1). Розглянемо упорядкований набір
) – розв’язки системи (1). Розглянемо упорядкований набір 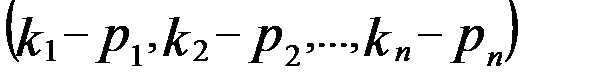 . Ми повинні довести, що це розв’язок системи (2).
. Ми повинні довести, що це розв’язок системи (2).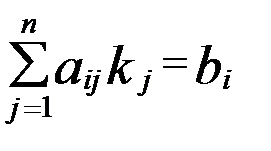 , (
, ( ), (3)
), (3) , (
, ( ). (3’)
). (3’) числа
числа  відповідно і обчислимо її.
відповідно і обчислимо її. .
. правильних числових рівностей.
правильних числових рівностей. – множина розв’язків системи (1),
– множина розв’язків системи (1), – множина розв’язків системи (2).
– множина розв’язків системи (2). - окремий розв’язок системи (1).
- окремий розв’язок системи (1). з будь-яким розв’язком однорідної системи.
з будь-яким розв’язком однорідної системи. +
+  =
=  ** є Н - розв’язок системи (1).
** є Н - розв’язок системи (1). є Н. Доведемо, що
є Н. Доведемо, що  можна одержати додаванням до
можна одержати додаванням до  якогось розв’язку з множини Q. Розглянемо різницю (
якогось розв’язку з множини Q. Розглянемо різницю ( -
- 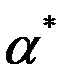 ). Тоді за теоремою 2, це розв’язок системи (2), тобто (
). Тоді за теоремою 2, це розв’язок системи (2), тобто ( -
-  ) =
) =  * є Q. Отже
* є Q. Отже  .
. розташованний в і-тому рядку та к-му стовпцю матриці С дорівнює сумі добутків елементів і-того рядка матриці А на відповідні елементти к-того стовпця матриці В.
розташованний в і-тому рядку та к-му стовпцю матриці С дорівнює сумі добутків елементів і-того рядка матриці А на відповідні елементти к-того стовпця матриці В. , В=
, В= 
 .
. , В=
, В=  .
. =
=  ,
,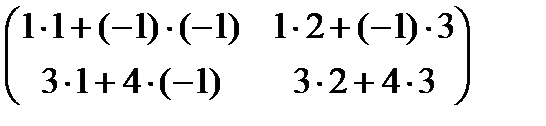 =
= 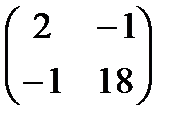 .
. ), В=(
), В=( ). А × В = D = (
). А × В = D = ( )
) ), (В × С) = Р (
), (В × С) = Р ( )
) ).
). (
( = 1,2,…,
= 1,2,…,  )
) , (1)
, (1) , (2)
, (2)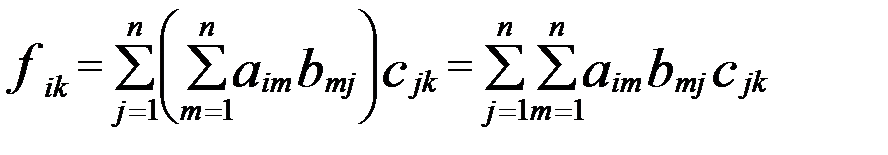 (3)
(3) .
. (4)
(4) (5)
(5) (6)
(6) , що й треба було довести.
, що й треба було довести. .
. ×
×  =
= = А.
= А. .
. .
. , тобто
, тобто , другий – на
, другий – на 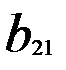 , n-ий – на
, n-ий – на  .
.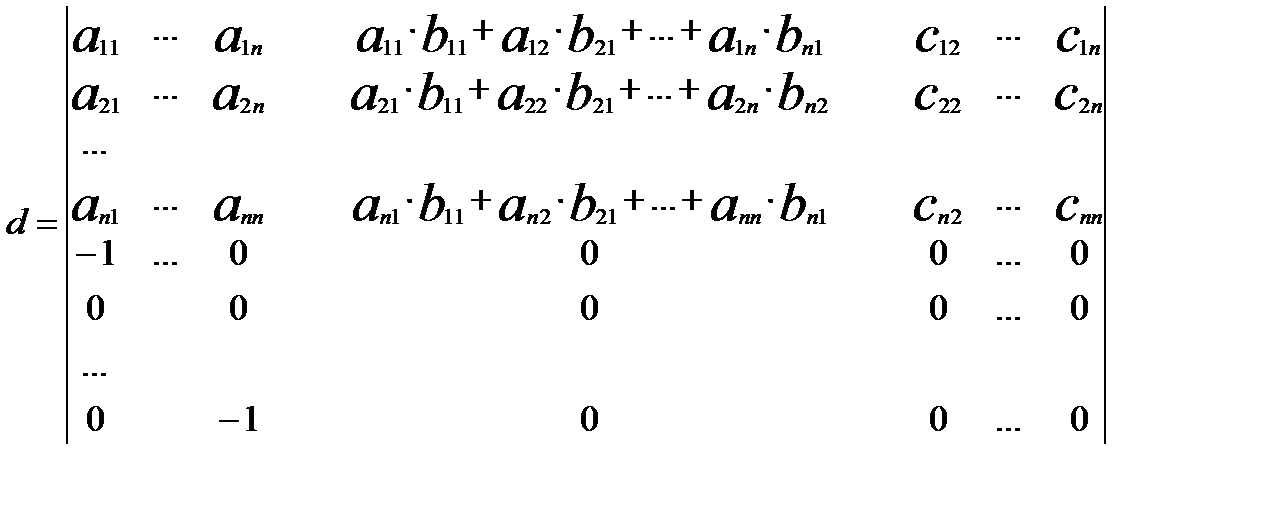

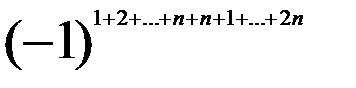 .
. , det C = det A × det B.
, det C = det A × det B.


