
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IV. Подвійний векторний добуток.
1. Поняття подвійного векторного добутку. Означення. Подвійним векторним добутком трьох векторів Алгебраїчні властивості подвійного векторного добутку є наслідками алгебраїчних властивостей векторного добутку. Існує зв’язок між подвійним векторним добутком і лінійними операціями над векторами. Цей зв’язок здійснюється за формулою
Доведення. (Довести цю формулу) Поняття лінійного простору. Означення 1. Г оворитимемо, що у множині М визначена внутрішня бінарна алгебраїчна операція, якщо будь-якій упорядкованій парі елементів Означення 2. Говоритимемо, що в множині M визначена зовнішня операція над множиною P, якщо будь-якій парі елементів Операція додавання векторів (геометричних) відноситься до внутрішніх операцій і операція множення геометричного вектора на число є прикладом зовнішньої операції, визначеної в множині геометричних векторів над множиною дійсних чисел. Означення 3. Векторним або лінійним простором називається непорожня множина V, в якій визначено дві операції над множиною дійсних чисел: внутрішня, що умовно називається додаванням, і зовнішня, що умовно називається множенням на дійсне число, і виконується 8 умов: 1. 2. 3. 4. 5. 6. 7. 8. Означення 4. Елементи множини V, що є векторним простором, називаються векторами. Приклад 1. Всі геометричні вектори простору (площини) утворюють векторний простір відносно традиційних операцій додавання геометричних векторів і множення вектора на число. Дійсно, виконання всіх вимог означення 3 було обґрунтовано у векторній алгебрі. Приклад 2. (арифметичний простір) За множину V візьмемо множину всіх упорядкованих
Числа Cумою векторів Добутком вектора
Можна показати за означенням, що арифметичний простір є лінійним простором. Контрприклад. За множину Vвізьмемо ту ж саму множину, що у прикладі 2. Операцію додавання введемо за тим же правилом. Операцію множення на число введемо іншим чином, а саме: добутком вектора В цій множині не виконується лише вимога 7.
Бачимо, Приклад 3. Розглянемо множину многочленів степеня не вищого за Операції додавання многочленів та множення на число вводиться традиційним способом. Легко перевірити виконання всіх вимог означення, тому дана множина є векторним простором відносно введених операцій. Контрприклад. Розглянемо множину многочленів лише У цьому випадку множина не є векторним простором, тому що в цій множині не визначена операція додавання. Дійсно, наведемо два многочленів, сума яких не є многочленом Наприклад, сума Приклад 4. Розглянемо множину всіх функцій, що визначені на проміжку Приклад 5. Розглянемо множину всіх функцій, що є неперервними на проміжку
Найпростіші властивості векторного простору. Властивість 1. У довільному векторному просторі існує лише один нульовий вектор. Доведення. Припустимо, що знайшовся такий векторний простір V, у якому декілька різних нульових елементів: Розглянемо суму За означенням нульового вектора За означенням нульового вектора Згідно із припущенням,
Властивість доведено. Властивість 2. У довільному векторному просторі для кожного вектора існує лише єдиний протилежний. Доведення. Припустимо, що у деякому векторному просторі Vзнайшовся вектор Розглянемо суму За означенням протилежного вектора За означенням протилежного вектора Згідно із припущенням, Властивість доведено. Надалі для зручності позначатимемо операції додавання і множення у векторному просторі як "+" і "
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.189.177 (0.011 с.) |
 називається векторний добуток двох векторів вектора
називається векторний добуток двох векторів вектора  і вектора
і вектора  :
:  .
.
 за деяким правилом ставиться у відповідність однозначно визначений елемент zϵM.
за деяким правилом ставиться у відповідність однозначно визначений елемент zϵM. ставиться у відповідність однозначно визначений елемент множини М.
ставиться у відповідність однозначно визначений елемент множини М. – комутативність додавання.
– комутативність додавання. – асоціативність додавання.
– асоціативність додавання. (
( x).
x). – для довільного елемента існує протилежний до нього.
– для довільного елемента існує протилежний до нього. – серед множини дійсних чисел є таке, що не змінює у добутку вектор.
– серед множини дійсних чисел є таке, що не змінює у добутку вектор.


 чисел.
чисел.
 назвемо компонентами вектора.
назвемо компонентами вектора. і
і  назвемо вектор, утворений сумою відповідних компонент:
назвемо вектор, утворений сумою відповідних компонент:  .
.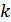 назвемо вектор
назвемо вектор  .
. .
.

 , отже ця множина не є лінійним простором.
, отже ця множина не є лінійним простором. та
та  є многочленом 1-го степеня.
є многочленом 1-го степеня. . Додавання і множення функцій на число введемо традиційним способом, як у математичному аналізі. При цьому також виконуються всі вимоги означення векторного простору, тому дана множина відносно введених операцій є векторним простором.
. Додавання і множення функцій на число введемо традиційним способом, як у математичному аналізі. При цьому також виконуються всі вимоги означення векторного простору, тому дана множина відносно введених операцій є векторним простором. і
і 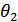 .
. .
. .
. .
. , для якого є декілька різних протилежних елементів:
, для якого є декілька різних протилежних елементів:  та
та  .
. . Скористуємось також асоціативністю додавання.
. Скористуємось також асоціативністю додавання.

 ", маючи на увазі абстрактні операції "
", маючи на увазі абстрактні операції "  " і "
" і "  ".
".


