
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторна робота № 2. Визначення модуля Юнга металів
МЕТА РОБОТИ: перевірити закон Гука; дослідним шляхом визначити модуль Юнга металевого дроту. ПРИЛАДИ І ЗНАРЯДДЯ: штангенциркуль, індикатор видовження, набір вантажів, дріт.
Вступ
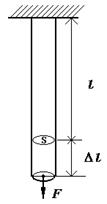
Під впливом прикладених зовнішніх сил будь-яке реальне тіло деформується, тобто змінює свої розміри та форму. Якщо після припинення дії зовнішніх сил тіло відновлює початкові розміри та форму, то така деформація тіла називається пружною. При пластичній деформації форма і розміри тіла не відтворюються після зняття навантаження. Пружні деформації спостерігаються в тому випадку, коли зовнішня сила, що обумовлює деформацію, не перевищує деякої певної межі – границі пружності. При пружних деформаціях під впливом прикладеного навантаження відбувається тільки незначна зміна відстаней між атомами, або повороти блоків кристалу. При розтягуванні кристалу атоми віддаляються, а при стискуванні наближаються один до одного. При такому зміщенні атомів з положень рівноваги порушується баланс сил притягування та відштовхування, тому після зняття навантаження зміщені атоми завдяки дії сил притягування, або відштовхування повертаються в початковий стан рівноваги і кристали приймають свою первинну форму та розміри. Прикладемо до твердого закріпленого з одного кінця стержня довжиною l зовнішню силу F (рис. 5.1). Нехай під впливом цієї сили стержень подовжиться на Δl. Відношення сили F до площі поперечного перерізу S
називається механічним напруженням s. У випадку циліндричного зразка (дроту) діаметром d площа перерізу дорівнює:
тому
Величина
називається відносною деформацією – це відношення абсолютного видовження
Рисунок 5.1
Експеримент показує, що в області пружних деформацій між величинами σ та ε має місце лінійна залежність. На рис. 5.2 ОА – область пружної деформації, де виконується закон Гука:
В області АВ – мають місце пластичні деформації, тобто при s> sт після припинення дії зовнішніх сил в тілі виникають залишкові деформації eзал. Напруження sт називається межею пружності матеріалу.
Рисунок 5.2
Залежність (5.4) відображає закон Гука, де Е називається модулем пружності, або модулем Юнга, який характеризує пружні властивості матеріалу. Він дорівнює механічній напрузі, при якій довжина стержня (дроту) подвоюється. Величина модуля Юнга головним чином визначається типом кристалічної гратки, тобто силами міжатомного зв’язку. Для деяких матеріалів величина Е приведена в таблиці 5.1.
Таблиця 5.1
Опис установки
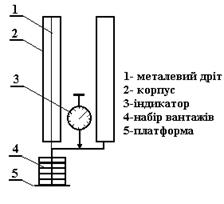
Схема експериментальної установки показана на рис.5.3.
Рисунок 5.3.
Дріт 1 закріплений у корпусі 2. До кінця дроту прикріплена платформа 5, на яку поміщуються вантажі 4. Видовження дроту вимірюється індикатором 3.
Порядок виконання роботи
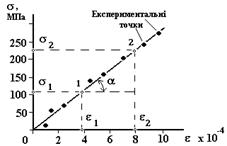
1. Для вирівнювання дроту навантажити його двома – трьома вантажами з набору. Обертаючи шкалу індикатора, встановити його показання на нуль. 2. Послідовно навантажуючи дріт усіма вантажами, вимірювати його абсолютне подовження Δl. Сила F=mg, що діє на дріт, дорівнюватиме сумарній вазі вантажів, покладених на платформу після установки нуля. Результати вимірювань m, Δl, занести в таблицю 5.2. 3. За формулами (5.2) і (5.3) розрахувати механічне напруження σ та відносну деформацію дроту ε. Результати розрахунків занести в таблицю 5.2. 4. Побудувати графік залежності σ = f(ε) за зразком, який представлено на рис. 5.4, тобто провести пряму так, щоб більшість експериментальних точок знаходились якнайближче до неї. На цій прямій (але не з таблиці!) вибрати будь-які дві точки 1 і 2, яким відповідають значення механічного напруження σ1, σ2 та відносної деформації ε1, ε2 .
Таблиця 5.2
Рисунок 5.4
4. За формулою:
розрахувати модуль Юнга Е. При такому методі визначення коефіцієнта пропорційності (як tga на рис.5.4) між будь-якими величинами, що лінійно залежать одна від одної, використовується вся сукупність експериментальних даних, а не випадкове значення якогось одного вимірювання. Користуючись даними таблиці 5.1 визначити матеріал, з якого виготовлено дріт. 5. Використовуючи теорію похибок, оцінити відносну похибку вимірювань модуля Юнга Е за формулою:
де величину δ l – похибку вимірювання видовження, розрахувати за формулою похибки для одноразових вимірювань:
розрахувати величини: D l ( 6. По виду графіка залежності σ = f(ε) зробити висновок, щодо справедливості закону Гука. Висновок повинен містити відповіді на запитання: Чи справедливий закон Гука і як це довести? Чому дорівнює модуль Юнга та похибка його вимірювань ( матеріалу виготовлено дріт?
Контрольні запитання
1. Дати визначення пружнім та пластичнім деформаціям. 2. Дати визначення механічного напруження s та відносної деформації e. 3. Який вид має експериментальний графік залежності 4. В чому полягає закон Гука? 5. Який фізичний зміст модуля Юнга?
Інструкцію склав доцент кафедри фізики Правда М.І. Рецензент - доцент кафедри фізики Манько В.К. Затверджена на засіданні кафедри фізики, протокол № 3 від 01.12.2008 р.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1081; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.134.107 (0.014 с.) |

 , (5.1)
, (5.1)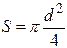 ,
, . (5.2)
. (5.2)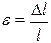 , (5.3)
, (5.3) до початкової довжини
до початкової довжини  .
.
 (5.4)
(5.4)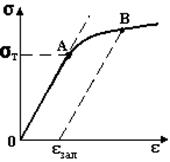
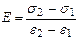 (5.5)
(5.5)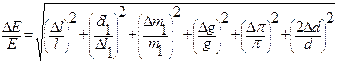 , (5.6)
, (5.6) , (5.7)
, (5.7)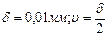 . За формулою похибки для табличних величин:
. За формулою похибки для табличних величин: . (5.8)
. (5.8) ), D m (
), D m (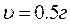 ), D g (
), D g (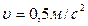 ), D p (
), D p (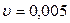 ), D d (
), D d (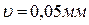 ).
). )? З якого
)? З якого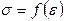 ?
?


