
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
До лабораторних робіт з фізикИСтр 1 из 13Следующая ⇒
Методичні вказівки До лабораторних робіт з фізикИ
Механіка. Молекулярна фізика Частина 1 Для студентів інженерно-технічних спеціальностей денної форми навчання
Методичні вказівки до лабораторних робіт з фізики. Механіка. Молекулярна фізика. Частина 1. Для студентів інженерно-технічних спеціальностей денної форми навчання / Укладачі: Лоскутов С.В., Єршов А.В., Серпецький Б.О., Правда М.І., Манько В.К., Лущін С.П., Курбацький В.П., Работкіна О.В., Денисова О.І. – Запоріжжя: ЗНТУ, 2009. - 90 с.
Укладачі: Лоскутов С.В., професор, д-р. фіз.-матем. наук.; Єршов А.В. канд. техн. наук, доцент; Серпецький Б.О., канд. фіз.-матем. наук, доцент; Правда М.І., канд. фіз.-матем. наук, доцент; Манько В.К.., канд. фіз.-матем. наук, доцент; Лущін С.П., канд. фіз.-матем. наук, доцент; Курбацький В.П., канд. фіз.-матем. наук, доцент; Работкіна О.В., старший викладач; Денисова О.І., старший викладач.
Р е ц е н з е н т и: Корніч В.Г., канд. фіз.-матем. наук; Золотаревський І.В., канд. фіз.-матем. наук, доцент; Сокол Т.О., старший викладач кафедри іноземної мови.
Затверджено на засіданні кафедри фізики ЗНТУ, протокол № 3 від 01.12.2008 р.
Методичні вказівки до лабораторних робіт з фізики “Механіка. Молекулярна фізика. Частина 1” схвалені на засіданні Методичної Ради Електротехнічного факультету ЗНТУ, протокол № 5 від ” 27 ” січня 2009 р.
Відповідальний за випуск: Єршов А.В., канд. техн. наук, доцент.
ЗМІСТ
Частина 1 Вступ …………………………………………………………………….. 6 1 Елементи теорії похибок ……………………………………………... 7 1.1 Основні поняття теорії похибок ……………………………………. 7 1.2 Похибки засобів вимірювання ……………………………………..11 1.3 Похибки табличних величин..…………………………….……. 12 1.4 Правила округлення і виконання наближених обчислень …..... 12 1.5 Похибки прямих вимірювань ……………………………………... 14 1.6 Похибки непрямих вимірювань …………………………………... 15 1.7 Графічне відображення експериментальних результатів …… 16 Контрольні запитання ……..…………………………………………... 17 2 Elements of the theory of errors …………………………………… 18 2.1 Principal concepts of the theory of errors …………………………… 19 2.2 Errors of instruments ………………………………………………. 20 2.3 Error of table quantities, count and rules of approximations...…...... 21 2.4 Errors of direct measurement ………..…………………………...... 21 2.5 Errors of indirect measurements …………………………..………… 22 2.6 Graph presentation of the experimental results …………….……...... 24 Control questions …………………………………….……….………… 24
3 Лабораторна робота № 1. Визначення густини тіл ………………... 25 3.1 Вступ ………………………………………………………………... 25 3.2 Вимірювання і визначення похибок ……………………………... 29 Контрольні запитання ……………..………………………..………… 31 4 Laboratory work № 1. Definition of a body density..………………… 34 4.1 System International Units …..……………………………………. 34 4.2 Volume ……………………………………………………………… 35 4.3 Vernier scale ………………………………………………………… 35 4.4 Micrometer screw gauge ………………………………………........ 36 4.5 Measurement of mass …………..………………………………….. 37 4.6 Measurement of weight …………………………………………….. 38 4.7 Experimental part …………………………………….……….…...... 39 5 Лабораторна робота № 2. Визначення модуля Юнга металів...... 41 5.1 Вступ…………………………….………………………………....... 41 5.2 Опис установки ……………………………………………………. 44 5.3 Порядок виконання роботи ……….………………………………. 44
Контрольні запитання ………………………………….…………….. 46 6 Laboratory work № 2. Measuring of Yung modulus of metals.……… 47 6.1 Introduction …………….…………………………………………. 47 6.2 Experimental device …………………….………………………...... 49 6.3 Experimental part ……………………………………………….... 50 Control questions ………….…………………………….…………........ 52 Literature ………………………………………………….…………… 52 7 Лабораторна робота № 3. Визначення коефіцієнта внутрішнього тертя методом Стокса ………………………….……….………… 53 7.1 Опис установки ………………………...……………. …………… 53 7.2 Теорія методу Стокса …………………………....……….……… 53 7.3 Порядок виконання роботи (завдання 1) …....………………..…... 54 7.4 Порядок виконання роботи (завдання 2) ……….………………. 55 Контрольні запитання …………………………………..…………....... 57 8 Laboratory work № 3. Measuring the coefficient of internal friction by Stocks’ method ……………………………...……………………58 8.1 Theory ………………………………………………...…………... 58 8.2 Experimental part ……………………………………...……………. 59 Control questions ………………………………………...…………........ 60 9 Лабораторна робота № 4.1 Пружний удар куль..…………………. 61 9.1 Коротка теорія пружного удару ……………………...…………. 61 9.2 Порядок виконання роботи ……………………………...………... 64
Контрольні запитання ……………….……………………………… 66 10 Лабораторна робота № 4.2. Пружний і непружний удари куль … 67 10.1 Основні положення …………………………………………… 67 10.2 Порядок виконання роботи ……………………………………… 72 Контрольні запитання …………………………………………………. 73 Список літератури ……………………………………………………... 73 11 Laboratory work № 4. Elastic impact of bodies.................................. 74 11.1 Task ……………………………………………………………... 74 11.2 Short theory...………………………………………………….... 74 11.3 Elastic impact ……………………….…………………………... 75 11.4 Experimental part ……………………………………………….. 77 Control questions ……………………………………………………… 77 12 Лабораторна робота № 4.3. Непружний удар тіл ………………… 79 12.1 Коротка теорія непружного удару …………………………….. 79 12.2 Порядок виконання роботи …………………………………… 81 Контрольні запитання …………...……………..……………………. 82 13 Laboratory work № 4.3. Inelastic impact of bodies ………………..84 13.1 Short theory of inelastic impact …………… …………………….84 13.2 The sequence of performing the work ………………………….. 87 Control questions …………………………………………………….. 88 Literature ………………………………….…………………………….. 88 Частина 2
ВСТУП
Збірник містить лабораторні роботи для студентів усіх спеціальностей. Основна спрямованість методичних вказівок з предмету фізика - дати можливість студентам за допомогою досліду вивчити важливі фізичні явища. Опис лабораторних робіт не претендує на те, щоб створити у студентів повне уявлення про явища, які вивчаються. Таке уявлення може виникнути лише внаслідок опрацювання лекцій та підручників. Велика увага в методичних вказівках з фізики для студентів технічних спеціальностей приділяється обробленню результатів вимірювання. Для успішного виконання робіт необхідна попередня самостійна підготовка, в першу чергу теоретична. Кожна лабораторна робота розрахована на дві академічні години занять у лабораторії. Перед заняттям студент повинен підготувати протокол лабораторної роботи, вивчивши відповідний теоретичний матеріал. Під час заняття студенти проводять необхідні виміри, виконують розрахунки, доводять звіт до висновку. Результати вимірювання обговорюються з викладачем і затверджуються. Повністю оформлений звіт по лабораторній роботі потрібно подати викладачу до кінця заняття. Він повинен містити: титульний лист, номер лабораторної роботи та її назву, перелік приладів і приладдя, мету роботи, схему установки, розрахункові формули, таблицю результатів вимірів і розрахунки, висновки за результатами роботи. Графіки повинні бути виконані на міліметровому папері. Якщо студент не встигає захистити лабораторну роботу до кінця заняття, дозволяється оформити звіт (графіки) з використанням комп’ютерних програм (Excel, Origin) до наступного заняття. Лабораторна робота вважається виконаною після успішно проведеного захисту шляхом співбесіди студента з викладачем (захист звіту + оцінка за теоретичний матеріал). Захист звіту: мета роботи + експериментальна методика + висновки. Теоретичний матеріал: знання фізичних явищ, які вивчалися у даній лабораторній роботі (закони, формули).
ЕЛЕМЕНТИ ТЕОРІЇ ПОХИБОК Похибки засобів вимірювання
До засобів вимірювань належать вимірювальні прилади та установки. Кожен прилад дає похибку, так як його неможливо зробити ідеальним. Похибка засобів вимірювання не перевищує деякої величини. Цю величину називають межею основної допустимої похибки вимірювального приладу (МОДП). МОДП на засоби вимірювання встановлюється державними стандартами і визначається у вигляді абсолютних, відносних та приведених похибок.
Абсолютна похибка приладу d – це є різниця
де a – показання приладу, X – справжнє значення вимірюваної величини. Взагалі d дорівнює ціні найменшої поділки інструмента. Наприклад: для лінійки d =1 мм. Відносна похибка вимірів – це відношення
Як правило, вона визначається у відсотках
Приведена похибка вимірювання або клас точності визначається відношенням
і визначається у відсотках. D – максимальне значення шкали інструмента. Наприклад: сила струму вимірюється амперметром з діапазоном 0 ÷ 1 А, клас точності 0,5. Це означає, що Хн = 1 А; γ = 0,5 % і
Якщо амперметр показує 0,3 А, тоді
Похибки табличних величин
1. Похибка табличної величини визначається за формулою
де a - довірча ймовірність; ν - половина ціни розряду останньої залишеної цифри табличної величини. Наприклад: величина π дорівнює 3,14. В цьому випадку ν = 0,005 і
Якщо величина π дорівнює 3,141 і ν = 0,0005, то
2. При користуванні вимірювальними приладами виникають похибки відліку. Типово, похибка відліку дорівнює половині ціни поділки шкали приладу. Наприклад: лінійка має похибку відліку ν = 0,5 мм.
Похибки прямих вимірювань
Похибки непрямих вимірювань
Якщо y - величина, що вимірюється посередньо, її розраховують за відомою залежністю y=f(x1,x2,…xn) від змінних x1,x2,,…xn, які вимірюють безпосередньо. 1. Похибки непрямих вимірів визначаються за формулою:
якщо функціональна залежність досліджуваної величини є багаточлен. 2. Похибки непрямих вимірів можна визначати
якщо функціональна залежність досліджуваної величини є одночлен і потім знаходимо Dy як: 1. Якщо залежність функції
Тоді
2. Якщо залежність функції:
Тоді
У результаті отримуємо
Errors of instruments
Absolute error of instrumental d is a deviation
where a is an index of an instrument; X is the true value of the quantity measured. Typically d is quantity of the instruments minimum value scale. For example: the ruler error is d = 1 mm. Relative error of the measurement is the ratio of
It is usually expressed in percent
Brought error of the measurement or precision class is the ratio
expressed in percent. D is maximum value on the instrument scale. For example: electric current is measured by the instrument with interval 0 ÷ 1 A, precision class is 0.5. This means, that D = 1 A, g = 0.5 %, and
If the instrument shows 0.3 A, then
Control questions
1. Definition of direct and indirect measurements. Examples. 2. Definition of the most probable value of the measured quantity x. 3. What is called a relative error? 4. What is called an accidental deviation? 5. What is the equation of square mean of errors? 6. How do we define errors of instruments? 7. How do we define errors of table quantities and count errors? 8. Rules of approximation. 9. What is the equation of errors of direct measurements? 10. What is the equation of errors of indirect measurements?
Authors: S.P. Lushchin, the reader, candidate of physical and mathematical sciences. Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences. Approved by the chair of physics. Protocol № 3 from 01.12.2008. Вступ
Густиною ρ э величина, що визначається для однорідної речовини (тіла) її масою в одиниці об'єму. Тобто для однорідного тіла знаходимо
де m – маса тіла, V – об’єм тіла. Масу тіла в лабораторній роботі визначають як табличне значення. Для обчислення густини тіла правильної геометричної форми проводимо вимірювання його лінійних розмірів. Далі обчислюємо об'єм за виміряними значеннями лінійних розмірів та відповідною формулою для тіла правильної геометричної форми. Нижче наведено формули об'ємів найпростіших геометричних фігур. Якщо це циліндр, то
де a – діаметр, h – висота циліндра. Для конуса
де a – діаметр основи, h – висота, π = 3,14. Для паралелепіпеда
де a, b, c три його ребра. Підставити в (3.1) відповідний об’єм і записати кінцеву робочу формулу
Найпростішим інструментом для вимірювання лінійних розмірів є лінійка. Її найменша поділка дорівнює 1 мм. Точність вимірювання за допомогою лінійки буде дорівнювати половині ціни поділки, тобто 0,5 мм. Для вимірювань із більш високою точністю використовують штангенциркуль та мікрометр. Підвищення точності досягається завдяки використанню допоміжної шкали – ноніуса. Штангенциркуль зображено на рисунку 3.1. Він складається з основної металевої лінійки 5 з міліметровими поділками. Па початку її розміщені нижня 6 та верхня 1 губки. Повзунок 4. нижня 7 та верхня 2 губки є одним цілим. Вони можуть переміщуватись уздовж основної лінійки 5 і фіксуватися в потрібному положенні за допомогою гвинта 3. На нижній частині повзунка 4 нанесені поділки ноніуса 8. Коли губки 6 і 7 стикаються, нуль лінійки і нуль ноніуса повинні збігатися.
1, 2 – верхні губки; 3 – фіксуючий гвинт; 4 – повзунок; 5 – лінійка; 6, 7 – нижні губки; 8 – ноніус. Рисунок 3.1 – Штангенциркуль
Другий тип штангенциркуля зображено на рис.3.2.
Цілі міліметри відраховуємо по основній шкалі до нульової риски шкали ноніуса. Долі міліметра зчитуємо по шкалі ноніуса по рисці, яка співпадає з будь-якою рискою основної шкали. Рисунок 3.2 – Штангенциркуль.
Для того щоб виміряти довжину предмета В, його розміщують між губками 6 і 7 і закріплюють гвинтом 3. Після цього проводять відлік по лінійці і ноніусу й обчислюють довжину предмета L за формулою (9). Для більш точного вимірювання розмірів предметів застосовуються мікрометричні гвинти з малим і точно витриманим кроком. Такі гвинти використовуються в мікрометрах. Мікрометр використовують для вимірювання зовнішніх розмірів із точністю до 0,01 мм.
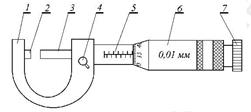
Мікрометр (див. рис. 3.3) складається зі скоби 1, що має па лівому кінці нерухому п'яту 2 (перша вимірювальна поверхня), а з іншого боку – втулку 5, всередині якої встановлено мікрометричний гвинт (шпиндель) 3 з кроком 0,5 мм. Торець цього гвинта 3 і є другою вимірювальною поверхнею. На зовнішній поверхні втулки 5 проведена осьова лінія, уздовж якої нанесені поділки лінійної шкали. Верхні і нижні штрихи лінійної шкали зміщені один відносно одного на півміліметра. Цифри проставлені тільки для поділок нижньої шкали, тобто вона є звичайною міліметровою шкалою. На втулку 5 надіто барабан 6, на скошену кільцеву поверхню якого нанесено шкалу ноніуса із 50 поділками. На голівці мікрометричного гвинта 3 є пристрій 7, що забезпечує сталість тиску на вимірювальний об'єкт. Цей пристрій 7 називається тріскачкою. Для фіксування положення мікрометричного гвинта використовується стопорний гвинт 4.
1 - скоба; 2 - нерухома п'ята; 3 – торець мікрометричного гвинта; 4 - стопорний гвинт; 5 - втулка з міліметровою шкалою; 6 - барабан зі шкалою ноніуса; 7 - тріскачка. Рисунок 3.3 – Мікрометр
Для того щоб виміряти довжину предмета, його розміщують між п'ятою 2 і торцем мікрометричного гвинта 3. Мікрометричний гвинт обертають, використовуючи тріскачку 7. При цьому мікрогвинт 3 та барабан 6 обертаються та переміщуються поступально відносно лінійної шкали на втулці 5. Обертання продовжується до зіткнення поверхонь вимірюваної деталі з вимірювальними поверхнями мікрометра 2 та 3, після чого тріскачка починає тріщати, а поступальний рух припиняється. Далі фіксують положення мікрогвинта 3 стопорним гвинтом 4. Зверніть увагу: обертати мікрометричний гвинт потрібно тільки користуючись тріскачкою 7. Інакше мікрометричний гвинт буде зірвано, мікрометр ушкоджено, вимірювання буде неправильним. Числове значення довжини вимірюваної деталі знаходять із формули:
де к – кількість поділок нижньої і верхньої лінійної шкали втулки, що відкриваються барабаном; b – відстань між сусідніми верхніми та нижніми поділками цієї шкали (0,5 мм); n – номер тієї поділки барабана, що у момент відліку збігається з осьовою лінією втулки; h – крок гвинта (0,5 мм); m – кількість всіх поділок (100) на шкалі ноніуса (барабана). Зверніть увагу: не можна починати вимірювання мікрометром, не перевіривши його початкове показання! Початкове показання мікрометра (тобто без вимірюваного тіла) повинне бути нульовим. Однак трапляються випадки, коли початкове показання мікрометра не дорівнює нулю. В такому разі потрібно визначити поправку до нульового значення (вона може бути як від'ємною, так і додатною величиною) і враховувати її під час вимірювань. Лінійний ноніус – це невелика лінійка С (рис. 3.4) із шкалою, m поділок якої дорівнюють m-1 поділкам основної шкали масштабної лінійки А. Звідси випливає, що ціна поділки основної лінійки b та ціна поділки ноніуса а пов'язані між собою співвідношенням
A - основна шкала; В - тіло, довжина якого вимірюється; С - шкала лінійного ноніуса. Рисунок 3.4 – Схема застосування ноніуса для вимірювання довжини тіла
Процес вимірювання полягає у такому. До нульової поділки шкали основної лінійки прикладають один кінець вимірюваною тіла В, а до іншого кінця тіла В – ноніус С. Тоді, як свідчить рисунок 3.4 шукана довжина тіла В буде дорівнювати
де розмір ΔL визначається з співвідношення (див. рис. 3.4):
Тут к – ціле число поділок масштабної лінійки; n – номер поділки ноніуса С, яка збігається з поділкою основної шкали А, Тоді з формул (3.7) і (3.8) отримуємо
Таким чином, довжина вимірюваного тіла дорівнює сумі двох величин: довжині к поділок основної шкали А, що розміщені зліва від нульової поділки ноніуса, та довжині, що дорівнює добутку точності ноніуса b/m на номер поділки ноніуса n, що збігається с поділкою основної шкали. System International units
A system of units, known as the System International (SI) units, is now used for all branches of physics. It is based on the meter as the unit of length, the kilogram as the unit of mass, the second as the unit of time, the ampere as the unit of electric current and the Kelvin as the unit of temperature. The unit of force in this system is the Newton and the unit of energy is the Joule. For many years the meter (m) was taken as the distance between two lines on a particular platinum-iridium rod at 00 C kept near Paris. It is now defined as the length of a certain number of wavelengths in a vacuum of a particular orange radiation of the krypton-86 atom. Unlike the distance between the marks on the rod, the wavelength of the radiation from an atom is a constant. By definition, 1 m = 1650763.73 wavelengths of the above radiation. The kilogram (kg) is the mass of a particular solid cylinder made of platinum-iridium alloy kept in Paris, known as the International Prototype Kilogram. In practice, the following smaller units may also be used. The millimeter (mm), which is 1/1000 m. The centimeter (cm), which is 1/100 m The gram (g), which is 1/1000 kg. The second (s) was formerly 1/86400 th part of a mean solar day. This unit, used by astronomers, has now been replaced by an atomic unit. Atomic clocks are now used as standard clocks. Clock which measured the period of rotation of the earth to an exceptionally high order of accuracy and this showed clearly the irregularity in the rate of rotation of the earth. Cesium or atomic clocks are now used as standard clocks. The second is defined as the time for 9192631770 cycles of vibration of a particular radiation from the caesium-133 atom. The mass per unit of volume of a substance is called its density:
where m is the mass of the body and V is its volume. The volume of a parallelepiped equals to:
where a, b, c are the width, the length and the height of the body. The volume of cylinder equals to:
where d is the diameter of base of a cylinder; h is the altitude of a cylinder. Thus we can calculate the density of a parallelepiped with the formula:
Or the density of a cylinder with the formula:
where m is the given mass of the body.
4.2 Volume
Measurements of volume were originally based on the litter; this is defined as the volume occupied by a mass of 1 kg of pure water at its temperature of maximum density and at standard atmospheric pressure. The milliliter (ml) is 1/1000 of a liter. In the SI system, however, volumes are based on the cube whose side is 1 m; that is the cubic meter. This volume is written m3. Volumes are also measured in cubic centimeters (cm3), although this is not an SI unit. 1 cm3 = 1 ml. Water has a density (mass/volume) of 1000 kg/m3 in SI units (equivalent to l g/cm3); mercury has a density of 13 600 kg/m3 in SI units (equivalent to 13.6 g/cm3).
4.3 Vernier scale
P. Vernier showed how lengths can be measured accurately. He used a subsidiary scale, now called a vernier scale. Fig. 4.1a shows the vernier scale Y below the main scale X, which is graduated in centimeters and millimeters. 10 divisions on Y make 9 mm. Thus the length between each division on Y is 0 ÷ 9 mm, which is 0.1 mm or 0.01 cm less than the length of the divisions on X. Fig. 4.1b shows the vernier scale Y moved to measure the length of a rod R. X
Figure 4.1 – Vernier scale
The length of R is greater than 8.2 but less than 8.3 cm. We now note the division S on Y which coincides with a division on M. This is the fourth division on Y. The third division on Y is thus 0.01 cm in front of the graduation B, the 2nd division on Y is 0.02 cm in front of the graduation C, and so on. Hence the zero of Y is MM cm in front of the 8.2 cm reading on M. Hence the length of R is 8.24 cm. Fig. 4.2 shows a form of vernier calipers. The object measured is placed between the jaws X and Y, and its length are read from the main and vernier scales as explained above.
Figure 4.2 –Vernier calipers
Micrometer screw gauge
The micrometer screw gauge is an instrument for measuring accurately the diameters of wires or thin rods. It uses an accurate screw of known 'pitch' such as 0÷5 mm, shown inset in Fig. 4.3. This means that for one revolution of the screw the spindle X moves forward or back 0÷5 mm.
Figure 4.3 – Micrometer gauge
To measure the diameter of a wire or rod A, one side is rested on the end Y and the thimble is turned until the end of the spindle X just touches A. Further turning of the thimble does not make the spindle move forward because a ratchet stops excessive pressure on A. A locking device is sometimes included so that the diameter reading can be read after A is taken out. An engraved linear millimeters scale L shows the forward movements of the spindle. A circular scale C on the thimble helps to measure fractions of millimeters. In Fig. 4.4, 50 circular divisions = 0.5 mm, or 1 circular division = 0.01 mm. So from Fig. 4.4, diameter of rod = 2.0 mm (scale L) + 46 × 0.01 mm (scale C) = 2.46 mm Some precautions are needed when using the screw-gauge to measure the diameter of a wire, for example (a) when the gap between X and Y is closed, check if the reading is zero; if not, add or subtract the error to your final reading of the diameter: (b) with the wire in the gap, make a firm but gentle contact with the screw, that is, do not over screw: (c) you should measure the diameter at three different places along the wire to allow for lack of uniformity; at each place, measure two perpendicular diameters to allow for any circular defect and then take the average of the six readings to get the diameter.
4.5 Measurement of mass
The mass of an object can be measured by comparing it with standard masses. These are derived from copies of the International Kilogram Mass. The chemical balance is used to compare masses in this way. Extremely sensitive balances can be designed. The National Physical Laboratory at Teddington in England has a balance which can measure to one-millionth of a gram. At this laboratory very precise weightings are carried out to assist science and technology. School balances do not require such high precision. The design of chemical balances has altered so much in recent years that the types used will generally differ from school to school. The top pan balance gives direct reading of mass. It does this by comparing the unknown mass with movable known masses inside it. As in the common balance, the unknown and known masses are balanced using a lever arrangement. If an object is taken say from London, England, to Lagos, Nigeria, or anywhere else in the world, and weighed on any other chemical balance, its mass will be exactly the same. So a chemical balance compares masses.
4.6 Measurement of weight
A spring balance provides a quick method of measuring weight. The object X (fig. 4.4) is hung from the hook and the spring is then pulled out by a length proportional to the weight of X. The weight of X is the force on X due to the earth's gravitational pull. The spring balance has a 'uniform' scale, that is equal divisions represent equal changes in weight along the whole scale. Weights are measured in Newtons (N) in SI units.
Figure 4.4 – Spring balance measuring weight
Unlike the chemical balance, the reading on the spring balance will vary slightly if the same mass is taken to different parts of the world. At the north; for example, it will weigh slightly more than at the equator. This is because gravitational pull is stronger at the poles and so the spring is stretched more. A spring balance measures weight, not mass.
Experimental Part
1. To measure length of the sides of the parallelepiped. One of the sides of it should be measured three times and two other sides are measured one time. 2. To fill results in to the table 4.1.
Table 4.1 – Dates for the parallelepiped
Table 4.2 – Dates for the cylinder
where ai (di) is the result of measurements; 3. To calculate the most probable meaning of density with the formula (4.1). 4. Mean root square:
5. At first it is necessary to obtain a formula for relative error:
where Δm is the error of a table quantity; Δa, Δb, Δc are half-widthes of the confidencal interval of direct measurements. 6. As we know:
where α is a probability; v is a half price of category from last significance figure in a table quantity. 7. As value of a is measured n times (n = 3) we use the formula:
where 8. Quantities of b and c we obtain by direct measuring and we measure b and c one time (n =1). So we have:
where v is an error of count;
10. To find ∆ρ from formula (4.7) in such a way:
where E is the relative error, calculated by formula (4.7); 11. To write down the result of measurement after approximation using the form:
Authors: S.P. Lushchin, the reader, candidate of physical and mathematical sciences. Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences. Approved by the chair of physics. Protocol № 3 from 01.12.2008. Вступ
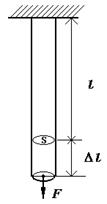
Під впливом прикладених зовнішніх сил будь-яке реальне тіло деформується, тобто змінює свої розміри та форму. Якщо після припинення дії зовнішніх сил тіло відновлює початкові розміри та форму, то така деформація тіла називається пружною. При пластичній деформації форма і розміри тіла не відтворюються після зняття навантаження. Пружні деформації спостерігаються в тому випадку, коли зовнішня сила, що обумовлює деформацію, не перевищує деякої певної межі – границі пружності. При пружних деформаціях під впливом прикладеного навантаження відбувається тільки незначна зміна відстаней між атомами, або повороти блоків кристалу. При розтягуванні кристалу атоми віддаляються, а при стискуванні наближаються один до одного. При такому зміщенні атомів з положень рівноваги порушується баланс сил притягування та відштовхування, тому після зняття навантаження зміщені атоми завдяки дії сил притягування, або відштовхування повертаються в початковий стан рівноваги і кристали приймають свою первинну форму та розміри. Прикладемо до твердого закріпленого з одного кінця стержня довжиною l зовнішню силу F (рис. 5.1). Нехай під впливом цієї сили стержень подовжиться на Δl. Відношення сили F до площі поперечного перерізу S
називається механічним напруженням s. У випадку циліндричного зразка (дроту) діаметром d площа перерізу дорівнює:
тому
Величина
називається відносною деформацією – це відношення абсолютного видовження
Рисунок 5.1
Експеримент показує, що в області пружних деформацій між величинами σ та ε має місце лінійна залежність. На рис. 5.2 ОА – область пружної деформації, де виконується закон Гука:
В області АВ – мають місце пластичні деформації, тобто при s> sт після припинення дії зовнішніх сил в тілі виникають залишкові деформації eзал. Напруження sт називається межею пружності матеріалу.
Рисунок 5.2
Залежність (5.4) відображає закон Гука, де Е називається модулем пружності, або модулем Юнга, який характеризує пружні властивості матеріалу. Він дорівнює механічній напрузі, при якій довжина стержня (дроту) подвоюється. Величина модуля Юнга головним чином визначається типом кристалічної гратки, тобто силами міжатомного зв’язку. Для деяких матеріалів величина Е приведена в таблиці 5.1.
Таблиця 5.1
Опис установки
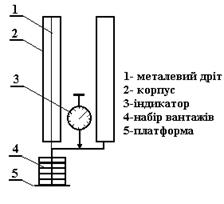
Схема експериментальної установки показана на рис.5.3.
Рисунок 5.3.
Дріт 1 закріплений у корпусі 2. До кінця дроту прикріплена платформа 5, на яку поміщуються вантажі 4. Видовження дроту вимірюється індикатором 3.
Порядок виконання роботи
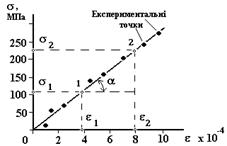
1. Для вирівнювання дроту навантажити його двома – трьома вантажами з набору. Обертаючи шкалу індикатора, встановити його показання на нуль. 2. Послідовно навантажуючи дріт усіма вантажами, вимірювати його абсолютне подовження Δl. Сила F=mg, що діє на дріт, дорівнюватиме сумарній вазі вантажів, покладених на платформу після установки нуля. Результати вимірювань m, Δl, занести в таблицю 5.2. 3. За формулами (5.2) і (5.3) розрахувати механічне напруження σ та відносну деформацію дроту ε. Результати розрахунків занести в таблицю 5.2. 4. Побудувати графік залежності σ = f(ε) за зразком, який представлено на рис. 5.4, тобто провести пряму так, щоб більшість експериментальних точок знаходились якнайближче до неї. На цій прямій (але не з таблиці!) вибрати будь-які дві точки 1 і 2, яким відповідають значення механічного напруження σ1, σ2 та відносної деформації ε1, ε2 .
Таблиця 5.2
Рисунок 5.4
4. За формулою:
розрахувати модуль Юнга Е. При такому методі визначення коефіцієнта пропорційності (як tga на рис.5.4) між будь-якими величинами, що лінійно залежать одна від одної, використовується вся сукупність експериментальних даних, а не випадкове значення якогось одного вимірювання. Користуючись даними таблиці 5.1 визначити матеріал, з якого виготовлено дріт. 5. Використовуючи теорію похибок, оцінити відносну похибку вимірювань модуля Юнга Е за формулою:
де величину δ l – похибку вимірювання видовження, розрахувати за формулою похибки для одноразових вимірювань:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.183.150 (0.26 с.) |
 , (1.13)
, (1.13) . (1.14)
. (1.14) . (1.15)
. (1.15) , (1.16)
, (1.16) .
.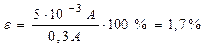 .
. , (1.17)
, (1.17) .
. .
.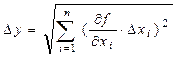 , (1.20)
, (1.20) , (1.21)
, (1.21) .
.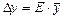 . Наприклад:
. Наприклад: , тоді
, тоді
 .
. ,
,
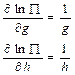
 ,
,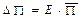 .
. .
. . (2.7)
. (2.7) . (2.8)
. (2.8) , (2.9)
, (2.9) .
. .
. ,
,  (3.1)
(3.1) , (3.2)
, (3.2)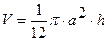 , (3.3)
, (3.3) , (3.4)
, (3.4) .
.

 , (3.5)
, (3.5)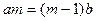 . (3.6) Величину
. (3.6) Величину  називають точністю ноніуса, вона дорівнює точності вимірювання.
називають точністю ноніуса, вона дорівнює точності вимірювання.
 , (3.7)
, (3.7) . (3.8)
. (3.8) . (3.9)
. (3.9) , (4.1)
, (4.1) , (4.2)
, (4.2) , (4.3)
, (4.3) (4.4)
(4.4) (4.5)
(4.5)



 = ∑ (∆аi)2 =
= ∑ (∆аi)2 =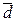 = ∑ (∆di )2 =
= ∑ (∆di )2 = (
( ) is the arithmetic mean; ∆аi (∆di) is the accidental error (deviation).
) is the arithmetic mean; ∆аi (∆di) is the accidental error (deviation). (4.6)
(4.6) (4.7)
(4.7) , (4.8)
, (4.8)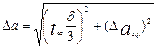 , (4.9)
, (4.9)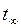 is the Student's constant; δ is an error of an instrument.
is the Student's constant; δ is an error of an instrument. ,
,  , (4.10)
, (4.10) .
. 9. To calculate quantities of Dm, Da, Db, Dc. Substituting them into formula (4.7), we find E.
9. To calculate quantities of Dm, Da, Db, Dc. Substituting them into formula (4.7), we find E. ,
, is the most probable meaning of the substance density, calculated by formula (4.1).
is the most probable meaning of the substance density, calculated by formula (4.1). =
=  …
… 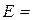 … %.
… %.
 , (5.1)
, (5.1)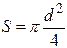 ,
, . (5.2)
. (5.2)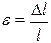 , (5.3)
, (5.3) до початкової довжини
до початкової довжини  .
.
 (5.4)
(5.4)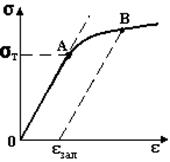
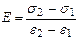 (5.5)
(5.5)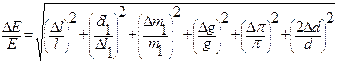 , (5.6)
, (5.6) , (5.7)
, (5.7)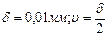 . За формулою похибки для табличних величин:
. За формулою похибки для табличних величин:


