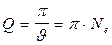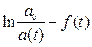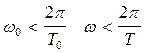Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение затухающих колебаний. Определение ⇐ ПредыдущаяСтр 10 из 10
Логарифм этического декремента затухания.
Цель работы: Экспериментальное определение логарифмического декремента затухания и добротности колебательной системы. Приборы и принадлежности: физический маятник, шкала с сантиметровыми делениями, секундомер.
ВВЕДЕНИЕ. Во всякой реальной колебательной системе имеются силы сопротивления, действия которых приводят к уменьшению энергии системы. Если убыль энергии не восполняется за счёт работы внешних сил, колебания будет затухать. В простейшем, случае сила сопротивления Fconp пропорциональна величине скорости. Fconp = - rх Здесь r — постоянная, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила Fconp и скорость и имеют противоположные направления, следовательно, их проекции на ось х имеют разные знаки. Уравнение второго закона Ньютона при наличии сил сопротивления в проекции наось х имеет вид:
Здесь первое слагаемое представляет собой проекцию квазиупругой силы на ось х, второе слагаемое — проекцию силы сопротивления на ось х. Применив обозначения
получим:
Это дифференциальное уравнение описывает затухающие колебания системы. Отметим, что w0 представляет собой ту частоту с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (при r =0). Эту частоту называют частотой собственных колебаний системы. Подстановка функции х =е-lt приводит к характеристическому уравнению
Корни этого уравнения равны
При не слишком большом затухании (при b < wо) подкоренное выражение будет отрицательным. Представим его в виде (iw)2 где <w> вещественная величина, равная
Тогда корни характеристического уравнения запишутся следующим образом:
a общим решением уравнения будет функция
или
Здесь а 0 и j - определяются начальными условиями.
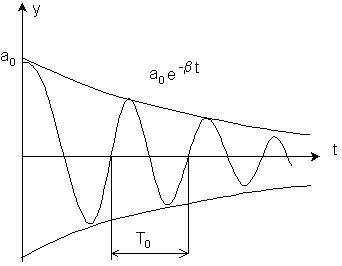
Рис.18
Движение системы можно рассматривать как гармоническое колебание частоты w с амплитудой, изменяющейся по закону a{t)= а 0 • е-bt. Верхняя из пунктирных кривых на рис1 даёт график функции а (t) причем величина а 0 представляет собой амплитуду в начальный момент времени. Начальное смещение x 0 зависит, кроме а 0, также от начальной фазы j: x0 = а 0 × cosj
Скорость затухания колебаний определяется величиной b =- r / 2m которую называют коэффициентом затухания.
При незначительном сопротивлении среды (b2 << w0) период колебаний, практически равен Т = 2p/w0. С ростом коэффициента затухания, период колебаний увеличивается. Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно:
Это отношение называют декрементом затухания, а его логарифм логарифмическим декрементом затухания:
Для характеристики колебательной системы обычно используется логарифмический декремент затухания J. Выразив b через J и Т, можно закон убывания амплитуды со временем записать в виде За время t, за которое амплитуда уменьшается в е раз, система успевает совершить Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в е раз. Для характеристики колебательной системы часто употребляется также величина
называемая добротностью колебательной системы. Как видно из её определения добротность пропорциональна числу колебаний Ne, совершаемых системой за то время t. за которое амплитуда колебаний уменьшается в е раз.
Измерения 1. Для определения зависимости амплитуды колебаний физического маятника от времени рекомендуется выбрать начальное отклонение маятника около 14 делений шкалы. Включить секундомер необходимо при значении амплитуды 12 делений и, не выключая его, отмечать время, когда амплитуда будет принимать значения равные 10, 8, 6, 4 и 2 делениям шкалы. 2. По полученным данным постройте график зависимости
Если амплитуда затухающих колебаний действительно уменьшается со временем по экспоненциальному закону, то точки на этом графике должны ложиться вдоль некоторой прямой. 3. По тангенсу угла наклона этой прямой определите коэффициент затухания b и найдите логарифмический декремент затухания и добротность системы. 4. Определите период Т затухающих колебаний, измерив время 50 полных колебаний физического маятника. Затем, сняв с маятника картонные «крылья», определите период То собственных колебаний маятника, измерив время 50 полных колебаний.
5. Вычислите 12. Данные измерений и вычислений внесите в таблицу.
Контрольные вопросы 1. Напишите дифференциальное уравнение затухающих колебаний. 2. Какой аналитический вид имеет зависимость амплитуды свободных затухающих колебаний физического маятника от времени? В каких координатах эта зависимость представляется прямой линией? 3. Как графически определить коэффициент затухания b? Как зная b вычислить логарифмический декремент затухания и добротность системы Q? 4. Как изменяется (увеличивается или уменьшается) период свободных колебаний при наличии сопротивления среды? 5. Какие колебания называются свободными? Чем определяется амплитуда, начальная фаза и частота свободных колебаний? 6. Как в данной работе определяется частота свободных колебаний? В чём отличие частоты свободных колебанийот частоты собственных колебаний? Когда они совпадают? 7. Что понимают под логарифмическим декрементом затухания? Каким образом эта величина определяется в работе?
ӘДЕБИЕТТЕР 1. Стрелков С.П. Механика. М., «Наука», 1975. 2. Савельев И.В. Курс общей физики, т.1, М., «Наука», 1973. 3. Архангельский М.М. Курс физики. Механика.М., «Просвещение» 1975. 4. Гершензон Е.М., Малов Н.Н., Курс общей физики. Механика.М., «Просвещение» 1978. 5. Руководство к лабораторным занятиям по физике. (Под редакцией Гольдина). М. «Наука», 1973. 6. Савельев И.В. Жалпы физика курсы. 1 том, Алматы, «Мектеп» 1977ж. 7. Арызханов Б. Физика курсы. Алматы, «Мектеп» 1988ж. 8. Тілеубергенова Г.А. т.б. Жалпы физика курсының практикумы. Алматы, «Мектеп» 1987 ж. 9. Қожанов Т.С., Рысменде С.С. Механика. Молекулалық физика. Термодинамика. Алматы 2000. 10. Хайкин С.Э. Физические основы механики. М. Наука. 1971. 11. Сивухин Д.В. Общий курс физики. М. 1989 Т.1 12. Физический практикум. Под ред. Ивероновой В.И. М.: Наука. 1967. 13. Богданова Т.Н., Субботина Е.Н. Руководство к практическим занятиям по физике. М.: Советская наука. 1949. 14. Келинков С.Г., Соломехо Г.И. Практикум по физике. М.: Высшая школа. 1990. 15. Майсова Н.Н. Практикум по курсу общей физики. М.: Высшая школа. 1970. 16. Ефремова Н.Н., Качан В.Л. Руководство к лабораторным работам по физике. М.: Высшая школа. 1970. 17. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике. М.: «Высшая школа». 1965. Литература 1. Стрелков С.П. Механика. М., «Наука», 1975. 2. Савельев И.В. Курс общей физики, т.1, М., «Наука», 1973. 3. Архангельский М.М. Курс физики. Механика.М., «Просвещение» 1975. 4. Гершензон Е.М., Малов Н.Н., Курс общей физики. Механика.М., «Просвещение» 1978. 5. Руководство к лабораторным занятиям по физике. (Под редакцией Гольдина). М. «Наука», 1973. 6. Хайкин С.Э. Физические основы механики. М. Наука. 1971. 7. Сивухин Д.В. Общий курс физики. М. 1989 Т.1 8. Физический практикум. Под ред. Ивероновой В.И. М.: Наука. 1967. 9. Богданова Т.Н., Субботина Е.Н. Руководство к практическим занятиям по физике. М.: Советская наука. 1949.
10. Келинков С.Г., Соломехо Г.И. Практикум по физике. М.: Высшая школа. 1990. 11. Майсова Н.Н. Практикум по курсу общей физики. М.: Высшая школа. 1970. 12. Ефремова Н.Н., Качан В.Л. Руководство к лабораторным работам по физике. М.: Высшая школа. 1970. 13. Кортнев А.В., Рублев Ю.В., Куценко А.Н. Практикум по физике. М.: «Высшая школа». 1965. Балабеков К.Н., Донбаев Қ.М., Жүнісбеков А.М., Қанымғазиева И.А., Киселев Б.Г.
Механика бөлімінен зертханалық жұмыстарға әдiстемелiк нұсқау /Оқу құралы/
Методические указания к лабораторным работам по механике
/Учебное пособие/
Техникалық редактор Жүнісбеков А.М. Шығаруға жауапты Балабеков Қ.Н.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 480; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.27.148 (0.019 с.) |
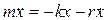
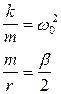
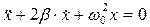
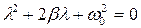
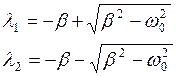
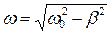
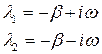
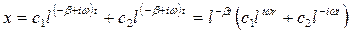
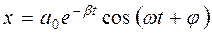

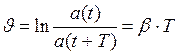
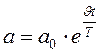 .
. колебаний.
колебаний.