
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила построения и обработки графиковСтр 1 из 10Следующая ⇒
Графики строятся на листе миллиметровой бумаги размером не меньше страницы тетради. На лист карандашом наносятся координатные оси, причем для независимой величины выбирается ось абсцисс. На концах осей указываются обозначения физических величин и единицы их измерения. Масштабные деления наносятся на оси в виде равноотстоящих «целых» чисел, кратных числам: 1, 2, 5,... или чисел, умноженных на 10± n (n — целое число). Обычно порядок масштаба, т. е. 10± n выносится на конец оси. Начало отсчета по осям и масштабы следует выбирать так, чтобы график занял все поле (не следует стремиться к тому, чтобы точка пересечения координатных осей соответствовала нулю по одной или по обеим осям: на графике приводится только та область изменения измеренных величин, которая была получена на опыте). После выбора начал отсчета по осям и масштабов на лист карандашом наносятся экспериментальные точки, которые соединяются плавной кривой без изломов и перегибов. Кривая должна проходить насколько возможно ближе ко всем нанесенным точкам, но ни в коем случае не следует стремиться провести ее через каждую точку; по обе стороны от кривой должно располагаться примерно одинаковое число точек. В экспериментах часто встречаются так называемые линейные зависимости 2-х измеряемых величин х и у: y = kx + b,
где k и b — постоянные параметры. График такой зависимости представляет собой прямую линию. Как правило, экспериментальные точки из-за различных погрешностей не ложатся на одну прямую. Задача экспериментатора — наилучшим образом провести прямую и по тангенсу угла наклона определить k ==D y /D x ==tg a.
Во многих случаях именно определение величины этого коэффициента является основной целью эксперимента. Правила взвешивания на весах
Для определениямасс существуетбольшое количество весов различной точности и пределов взвешивания. Обычно различают технические весы, точность которых составляет несколько миллиграммов и аналитические весы, точность которых может составлять десятые и сотые доли миллиграмма. Однако, в общих чертах устройство тех и других весов одинаково. Основой весов является коромысло, установленное на призме и к концам которого подвешены чашки. В нерабочем состоянии весы арретируются. С помощью специального приспособления коромысло весов приподнимается с острия призмы специальными колонками. Это делается для того, чтобы уменьшить изнашивание призмы и предохранить её от толчков и ударов. Отличие аналитических весов от технических заключается в том, что аналитические весы заключаются в шкафчик с прозрачными (стеклянными) стенками, чтобы исключить искажения, связанные с движением воздуха.
Кроме того, аналитические весы обычно снабжаются специальнымлегким проволочным разновесом - "гусариком'', или "рейтером", который может устанавливаться в любой точке коромысла весов. Весы должны устанавливаться строго по отвесу. Любая неточность установки приведёт к отклонению стрелки от вертикали и появлению систематической ошибки взвешивания. При ненагруженных весах стрелка устанавливается вертикально около нулевого положения шкалы. Обычно при этом стрелка с нулевым положением не совпадает, поэтому прежде чем взвешивать, нужно определить нулевое положение стрелки, и определить цену деления шкалы с помощью, разновесов. Изменять нагрузку весов можно только при арретированных весах. Брать разновески и взвешиваемые тела следует пинцетом. До окончательного установления весов не освобождать арретир полностью. Для исключения систематической ошибки весов используется несколько методов: 1. Метод двойного взвешивания. Тело взвешивается сначала на одной чашке весов, затем на другой. Результат находится как среднее арифметическое двух взвешиваний. 2. Метод тарирования. Тело уравновешивается обычно песком, насыпаемым на вторую чашку весов. После этого тело снимается и заменяется разновесками. 3. Разновидность метода тарирования является метод постоянной нагрузки. При этом на одной чашке весов находится постоянная гиря, масса которой больше массы взвешиваемых тел. На второй чашке помещаются разновески, которые уравновешивают гирю. Затем на вторую чашку помещают взвешиваемое тело, а часть разновесок убирают до получения нового равновесия.
Измерение линейных размеров.
Штангенциркуль, микрометр.
В простейшем случае измерение длины осуществляется простым сравнением эталона (масштабной лин ейки) с измеряемой длиной. Повышение точности измерения сводится с устранению возможных источников ошибок. При работе со шкалой такими ошибками могут быть неравномерность шкалы, толщина штрихов шкалы, параллакс (кажущее совпадение штриха шкалы и границы линии из-за смещения глаза наблюдателя) и т.д. Все усовершенствования измерительных приборов в этом случае сводятся к устранению источников ошибок и уменьшению деления шкалы. Штангенциркуль. Штангенциркуль представляет собой линейку с делениями, снабженную двумя зажимами (губками) между которыми помещается измеряемое тело. Один из зажимов неподвижный, с ним связывается нулевой отсчет линейки, второй зажим скользит по линейке, соответственно размерам тела.
Рис. 1 Штангенциркуль.
Обычно все приборы, имеющие шкалу снабжаются нониусом. Как уже говорилось, ошибка при измерении по шкале принимается равной половине деления шкалы. Такая оценка связана с тем, что глаз человека может определять часть деления шкалы с точностью около 0,15-0,20 деления. С учетом того, что не всегда концы измеряемого тела совпадают со штрихами шкалы принята такая оценка погрешности. Однако, точность измерения при тех же делениях шкалы может быть существенно увеличена. Два штриха шкалы можно совместить с точностью до половины ширины штриха. Если ширина штриха составляет 0,05 основного деления, то совмещать штрихи можно с точностью в 0,05 величины основного деления. Для этого подвижный зажим соединяется с дополнительной шкалой. Шкала эта конструируется таким образом, чтобы длина, соответствующая n делениям основной шкалы разбивалась на дополнительной шкале на n -1 или n +1 делений. Таким образом одно деление дополнительной шкалы (нониуса) отличается на 1/ n от деления основной шкалы. Если деление нониуса меньше деления основной шкалы, то нониус называется прямым или нониусом первого рода. Если деление нониуса больше деления шкалы, то нониус называется обратным или нониусом второго рода.
Нониус первого рода
Рис.2
Если теперь длина предмета отличается на ∆ L от целого числа делений шкалы, то нетрудно видеть, что совпадут - D L / n деление нониуса и штрих шкалы. Это даёт возможность повысить точность измерения в 20-10 раз по сравнению с обычной шкалой. Нониусы различной конструкции применяются практически во всех случаях измерения угловых и линейных величин. Хотя при этом их конструкции могут существенно отличаться, принцип всех нониусов один – повышение точности совмещения шкалы с измеряемым телом за счёт ширины штриха шкалы. Микрометр. Микрометрический винт. При измерениях малых длин помимо точности отсчета необходимо фиксировать очень малые перемещения подвижного зажима. Обычно это осуществляется с помощью микрометрического винта. Микрометрический винт – это винт с относительно большим диаметром и малым шагом. Один оборот винта перемещает зажим на малое расстояние, равное шагу. Однако благодаря большому диаметру можно разделить окружность винта на большое число. делений (обычно 50-100 делении) и отсчитывая с помощью этих делении часть оборота винта соответственно перемещать его на соответствующую часть шага. При шаге винта 0,5 мм и разделении окружности винта на 50 делении это даёт возможность измерять толщины с точностью 0,01 мм. Шкала микрометрического винта обычно не снабжается нониусом, так как неточности шага винта и качество резьбы обычно оказывается больше, чем часть шага, соответствующая толщине штриха.
Микрометр Рис.3
Микрометр представляет собой жесткую металлическую скобу одна сторона которой снабжена неподвижным зажимом, а вторая подвижным зажимом, связанным с микрометрическим винтом. При работе с микрометром очень важно обеспечить одинаковое усилие сжимающее измеряемое тело при всех измерениях. С этой целью рукоятка микрометрического винта связана с самим винтом фрикционной передачей – трещеткой Другим способом повышения точности линейных измерений является использование отсчетных микроскопов. В этом случае шкала помещается в фокусе окуляра микроскопа. Увеличение объектива в этом случае дает возможность более точно совмещать деление шкалы и границы измеряемого тела. А увеличение окуляра дает возможность использовать шкалу с более мелким делением. Лабораторная работа № 1 Погрешности измерений
Цель работы: ознакомиться с методами определения относительных и абсолютных ошибок прямых и косвенных измерений. Получить представление о систематических ошибках и их учете. Получить представление об оптимальном выборе условий измерения. Приборы и материалы: установка ЕLWRO для изучения ошибок измерений. Измерения Работа заключается в измерении удельного сопротивления материала проволоки и оценке возникающих при этом погрешностей. Как известно, из школьного курса физики, сопротивление проводника определяется формулой
где R- сопротивление проводника, l - его длина, S - площадь поперечного сечения, r - удельное сопротивление. Сопротивление можно определить, измеряя силу тока и падение напряжения на проводнике. Тогда удельное сопротивление находится как
Это типичный пример косвенного измерения, так как при этом измеряются сила тока, напряжение, длина и диаметр проволоки, а удельное сопротивление находится из вычислений. Установка ЕLWRO для измерения, удельного сопротивления включает в себя проводник, для которого собственно измеряется удельное сопротивление, выпрямитель со стабилизатором тока, линейку для измерения длины проводника, между электрическими контактами один из которых подвижный, амперметр, вольтметр. Для проверки полученного результата к установке может подключатся мостовая схема измерения сопротивлений.
Амперметр и вольтметр могут подключаться к проводнику двумя способами
Нетрудно видеть, что каждый из способов вносит свою систематическую погрешность. В первом способе вольтметр измеряет сумму падений напряжения на проводнике и на амперметре, т.е, получается завышенное напряжение. Во втором случае амперметр измеряет силу тока, протекающего не только через проводник, но и через вольтметр, что дает завышенную силу тока. Принимая во внимание, что измеряется небольшое сопротивление короткого проводника, следует считать, что в первом случае ошибка будет больше, так как сопротивления проводника и амперметра сравнимы по величине, тогда как сопротивление вольтметра много больше сопротивления проводника. 1. Включить установку в сеть, прогреть ее в течение 10-15 минут. 2. Установить длину проводника 40-50 см. Изменяя силу тока через 10мА, измерить разность показаний вольтметра при первом и втором способах включения. Если действительно сопротивление вольтметра очень велико, то зависимость 3. Установить длину проводника 10см. Для первого способа включения измерить падение напряжения на проводнике при силе тока 65 мА, 100 мА, 150 мА, 200 мА, 250 мА. Занести результаты в таблицу и вычислить для каждого значения тока полученное удельное сопротивление. Взяв из графика соответствующую поправку исправить полученное значение U и вычислить исправленное значение удельного сопротивления. При вычислении считать диаметр проволоки 0,155мм. 4. Повторить измерение для длин проволоки 20, 30, 40 и 50см.
Результаты занести в таблицу. J = 65 м А.
J = 100 м А.
J = 150 m A J = 200 m A J = 250 m A Относительная ошибка в определении удельного сопротивления определится как
5. Определить среднее значение и среднеквадратичные ошибки измерений для каждого раздела таблицы (для каждой силы тока) и для всех измерений вместе взятых. Сравнить полученные из разброса полученных результатов расчетные значения. Среднеквадратичная ошибка может оказаться меньше расчётной это связано с тем, что ошибка измерений амперметра и вольтметра носит в значительной степени систематический характер и может не проявляться как случайная. Например, если амперметр во всей шкале даёт показания, отличающиеся на некоторую величину от истинных, то такая ошибка не обнаружится. Однако, она обусловлена классом точности прибора и поэтому должна учитываться.
Контрольные вопросы
1. Какие измерения называются прямыми и какие косвенными? 2. Что такое случайные и что такое систематические ошибки, чем они обусловлены? 3. Что такое среднеквадратичная ошибка и как она определяется? 4. Что такое доверительный интервал? 5. Как определяется ошибка косвенных измерений?
Лабораторная работа №2
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.120.109 (0.033 с.) |




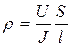




 R
R
 R
R

 Построить график зависимости
Построить график зависимости  от J (правила построения графиков).
от J (правила построения графиков).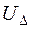 от J должна проходить вблизи начала координат что и дает возможность учитывать систематическую ошибку, обусловленную внутренним сопротивлением вольтметра.
от J должна проходить вблизи начала координат что и дает возможность учитывать систематическую ошибку, обусловленную внутренним сопротивлением вольтметра.








