
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динаміка криволінійного руху
183. Із якого рівняння можна визначити значення першої космічної швидкості? А) 184. Із якого рівняння можна визначити значення другої космічної швидкості? А) 185. Визначте першукосмічну швидкість для Венери, якщо маса Венери МВ становить 4,9×1024 кг, а її радіус RB дорівнює 6200 км.
А) 6,8 км/с. Б) 4,9 км/с. В) 7,3 км/с. Г) 8,1 км/с. Д) 7,8 км/с.
186. Обчисліть прискорення вільного падіння gh тіл на висоті h, яка дорівнює половині радіуса Землі. Радіус Землі R3 вважати рівним 6400 км.
А) 6,82 м/с2. Б) 8,46 м/с2. В) 5,78 м/с2. Г) 7,19 м/с2. Д) 4,34 м/с2.
187. Яку швидкість V повинен мати супутник, щоб обертатись навколо Землі на висоті h =600 км над її поверхнею? Який період його обертання? Радіус Землі R3 =6400 км, а її маса М3 =6×1024 кг. А) 6,8×103 м/с. Б) 8,0×103 м/с. В) 7,2×103 м/с. Г) 7,6×103 м/с. Д) 6,4×103 м/с.
188. Визначити період T обертання супутника навколо Землі, якщо він обертається на висоті h =1700 км над її поверхнею? Радіус Землі R3 вважати рівним 6400 км.
А) 100 хв. Б) 60 хв. В) 120 хв. Г) 40 хв. Д) 80 хв.
189. Місяць рухається навколо Землі зі швидкістю V =1 км/с. Відстань R від Землі до Місяця дорівнює 3,8×105 км. Визначите за цих умов масу Землі M3.
А) 5,7×1024 кг. Б) 6,1×1024 кг. В) 5,5×1024 кг. Г) 5,9×1024 кг. Д) 6,3×1024 кг.
190. Автомобіль масою m =2 т проходить по опуклому мосту, радіусом R =40 м, зі швидкістю V =36 км/год. Із якою силою N давить автомобіль на міст у його середині? (Вважати g =10 м/с2).
А) 25 кН. Б) 20 кН. В) 10 кН. Г) 30 кН. Д) 15 кН.
191. Із якою швидкістю V має їхати велосипедист у середній частині опуклого мосту із радіусом кривини R =10 м, щоб не чинити тиску на міст? (g =10 м/с2).
А) 15 м/с. Б) 10 м/с. В) 25 м/с. Г) 20 м/с. Д) 30 м/с.
192. Тіло масою m =1 кг рухається по колу радіуса R =2 м у вертикальній площині. Чому дорівнює сила натягу нитки Fн у нижній точці кола, якщо його швидкість у цій точці V =4 м/с? (Вважати g =10 м/с2).
А) 24 Н. Б) 12 Н. В) 32 Н. Г) 18 Н. Д) 36 Н.
193. Із якою найбільшою швидкістю Vmax можна вести автомобіль на повороті дороги із радіусом кривини R =150 м, щоб його “не занесло”, якщо коефіцієнт тертя коліс об дорогу m =0,42?
А) 25 м/с. Б) 30 м/с. В) 35 м/с. Г) 15 м/с. Д) 20 м/с.
194. Льотчик тисне на сидіння крісла літака у верхній точці петлі Нестерова із силою N =6300 Н. Маса льотчика m =70 кг, а радіус петлі R =400 м. Визначити швидкість літака V. (Вважати g =10 м/с2).
А) 150 м/с. Б) 200 м/с. В) 300 м/с. Г) 250 м/с. Д) 100 м/с.
195. Літак здійснює «мертву петлю» радіусом R =800 м, рухаючись зі сталою швидкістю V =720 км/год. 3 якою силою N пілот масою m =70 кг буде тиснути на сидіння літака у верхній точці петлі?
А) 6300 Н. Б) 3700 Н. В) 2800 Н. Г) 5400 Н. Д) 4200 Н.
196. Літак, рухаючись зі швидкістю V =720 км/год, робить "мертву петлю" радіусом R =800 м. З якою силою N пілот масою m =70 кг давить на сидіння літака у нижній точці траєкторії руху?.
А) 6400 Н. Б) 2700 Н. В) 3800 Н. Г) 4200 Н. Д) 5400 Н.
197. Відро, до половини наповнене водою, обертають у вертикальній площині. Відстань від осі обертання до центру його ваги R =1 м. Із якою найменшою частотою nmin потрібно обертати відро, щоб вода у верхній точці не виливалась із нього?
А) 0,25 Гц. Б) 1,0 Гц. В) 0,75 Гц. Г) 1,25 Гц.. Д) 0,50 Гц.
198. Із якою максимальною швидкістю Vmax може їхати мотоцикліст по горизонтальній площині, описуючи дугу радіусом R =90 м, якщо коефіцієнт тертя коліс об дорогу m дорівнює 0,4?
А) 14,5 м/с. Б) 18,8 м/с. В) 22,4 м/с. Г) 27,6 м/с. Д) 16,3 м/с.
199. На який кут a від вертикалі повинен відхилитись мотоцикліст, описуючи дугу радіусом R =90 м, при швидкості руху V =15 м/с? (Вважати g =10 м/с2).
А) 140. Б) 220. В) 300. Г) 180. Д) 260.
200. Визначити доцентрове прискорення ац тіла на екваторі, що пов'язане із добовим обертальнім рухом Землі. Радіус Землі R3 вважати рівним 6400 км.
А) 5,1×10-3 м/с2. Б) 6,8×10-2 м/с2. В) 9,6×10-3 м/с2. Г) 3,4×10-2 м/с2. Д) 1,7×10-2 м/с2.
201. Мотоцикліст рухається зі швидкістю V =80 км/год по горизонтальному кільцю вертикального циліндру, радіусом R =10 м. Яким повинен бути мінімальний коефіцієнт тертя шин мотоцикла об поверхню циліндра m, щоб таке було можливим?
А) 0,05. Б) 0,10. В) 0,25. Г) 0,15. Д) 0,20.
202. Який мінімальний радіус кола R, по якому може проїхати ковзаняр, що рухається зі швидкістю V =20 км/год, якщо коефіцієнт тертя ковзанів об лід m =0,2?
А) 12,8 м. Б) 21,6 м. В) 15,7 м. Г) 18,2 м. Д) 24,4 м.
203. Літак рухається по колу у горизонтальній площині зі швидкістю V =720 км/год. Визначте радіус цього кола R, якщо корпус літака повернутий навколо напрямку його польоту на кут a =100. (Вважати g =10 м/с2).
А) 22,7 км. Б) 16,4 км. В) 25,2 км. Г) 18,8 км. Д) 20,6 км.
204. Хлопчик масою m =50 кг коливається на гойдалці iз довжиною підвісу l =4 м. З якою силою N він давить на сидіння при проходженні середнього положення зі швидкістю V =6 м/с? А) 500 Н. Б) 950 Н. В) 800 Н. Г) 650 Н. Д) 900 Н.
205. Знайти силу тиску N автомобіля на середину опуклого мосту, радіусом R =50 м, якщо його маса m дорівнює 5 т, а швидкість V =21,6 м/с.
А) 3,0 кН. Б) 1,8 кН. В) 4,2 кН. Г) 2,4 кН. Д) 3,6 кН.
206. Шосе має віраж з ухилом a =100 при радіусі заокруглення дороги R =100 метрів. На яку швидкість руху V розрахований цей віраж?
А) 15,4 м/с. Б) 18,2 м/с. В) 13,1 м/с. Г) 16,5 м/с. Д) 14,7 м/с.
207. Тягарець математичного маятника рухається по колуу горизонтальній площині так, що нитка підвісу описує конус. Відстань від точки підвісу до центру кола h =10 см. Обчисліть кількість обертів тягарця N за Dt =1 хвилину. (g =10 м/с2).
А) 95,5. Б) 72,8. В) 64,6. Г) 86,4. Д) 58,2.
Динаміка обертального руху
208. Яка із величин, що характеризують обертальний рух, еквівалентна масі при поступальному русі? А) Момент імпульсу. Б) Кутове прискорення. В) Момент сили. Г) Момент інерції. Д) Кутова швидкість. 209. Чим визначається момент інерції твердого тіла відносно даної осі обертання? А) Кутовою швидкістю тіла. Б) Моментом імпульсу тіла. В) Кутовим прискоренням тіла. Г) Моментом сил, що діють на тіло. Д) Розподілом маси тіла відносно даної осі.
210. Від яких чинників не залежить момент інерції твердого тіла?
А) Від форми тіла. Б) Від кутової швидкості обертання. В) Від маси і розмірів тіла. Г) Від вибору осі обертання. Д) Від маси тіла.
211. Момент інерції твердого тіла залежить від:
А) Моменту сили і кутового прискорення тіла. Г) Величини сили і плеча цієї сили. Б) Моменту імпульсу і кутової швидкості. Д) Величини сили і кутового прискорення. В) Маси тіла і її розподілу відносно осі обертання.
212. Укажіть невірну розмірність для моменту інерції тіла. А) Н м2. Б) кг м2. В) Н×м×с2. Г) Дж×с2. Д) 213. Укажіть математичний вираз теореми Штейнера для визначення моменту інерції твердого тіла ( d - відстань від центра мас тіла до осі його обертання). А) 214. Чому дорівнює момент інерції обруча масою m відносно осі, перпендикулярної до його площини, яка проходить через кінець радіуса R? А) 215. Чому дорівнює момент інерції кулі масою m =1 кг і радіусом R =10 см відносно осі, дотичної до її поверхні? А) 0,8×10-2 кг×м2. Б) 1,2×10-2 кг×м2. В) 1,4×10-2 кг×м2. Г) 2,2×10-2 кг×м2. Д) 1,8×10-2 кг×м2.
216. Чому дорівнює момент інерції диска щодо осі, яка проходить через середину радіуса перпендикулярно його площині? (m - маса диска, R - його радіус).
А) I=0,5mR2. Б) I=0,75mR2. В) I=mR2. Г) I=1,5mR2. Д) I=0,25mR2.
217. Розрахувати момент інерції суцільного циліндра із рівномірно розподіленою масою відносно осі, яка співпадає із однією із твірних його бокової поверхні. Маса циліндра m =1 кг, а радіус R =10 см.
А) 1,5×10-2 кг×м2. Б) 2×10-2 кг×м2. В) 0,5×10-2 кг×м2. Г) 5×10-2 кг×м2. Д) 2,5×10-2 кг×м2.
218. Визначити момент інерції тонкого однорідного стрижня завдовжки l =1,2 м і масою m =1 кг відносно перпендикулярної стрижню осі, яка проходить на відстані d =20 см від одного із його кінців.
А) 0,12 кг×м2. Б) 0,42 кг×м2. В) 0,36 кг×м2. Г) 0,28 кг×м2. Д) 0,18 кг×м2.
219. На одному кінці стрижня завдовжки l =0,5 м закріплений вантаж, розмірами якого можна знехтувати. Маса вантажу m1 =0,5 кг, а стрижня m2 =200 г. Визначте момент інерції І цієї системи щодо перпендикулярної стрижнюосі, яка проходить через інший його кінець. А) 0,18 кг×м2. Б) 0,32 кг×м2. В) 0,08 кг×м2. Г) 0,24 кг×м2. Д) 0,14 кг×м2. 220. Порожнистий циліндр радіусом R =0,1 м має довжину твірної l =0,2 м. Порівняйте моменти інерції цього циліндра І0 та І відносно двох осей: 1) Вісь співпадає з віссю самого циліндра; 2) Вісь перпендикулярна твірній циліндра і проходить через його край. А) 221. Тонкостінний обруч радіусом R =0,5 м і масою m =1 кг підвішений на тонкому горизонтальному стрижні. Розрахувати момент інерції обруча відносно осі, яка співпадає із стрижнем.
А) 0,25 кг×м2. Б) 0,375 кг×м2. В) 0,50 кг×м2. Г) 0,125 кг×м2. Д) 0,725 кг×м2.
222. Укажіть одиницю виміру моменту сили. А) 223. Яке із наведених співвідношень визначає величину моменту сили, прикладеного до тіла? А) m×r2. Б) 224. При виконанні лабораторної роботи на маятнику Обербека (по динаміці обертального руху твердого тіла) студенти намотують нитку по черзі на два шківи різних радіусів. Яка величина змінюється при цьому?
А) Момент інерції маятника. Б) Момент імпульсу системи. В) Маса системи. Г) Момент діючої на систему сили. Д) Потенціальна енергія системи.
225. Визначити момент сили М щодо осі обертання барабану радіуса R, якщо вантаж масою m, підвішений до кінця намотаної на нього нитки, рухається вниз рівномірно. А) M=2m×g×R. Б) M=m×(g-a) R. В) M=m×g×R. Г) M=m×(g+а) R. Д) M=2m×(g-а) R.
226. Визначте момент сили M щодо осі обертання барабану, якщо до кінця намотаної на нього нитки прив'язаний вантаж вагою Р, який опускається iз прискоренням а. Радіус барабану r. А) 227. Чому дорівнює момент сили М, діючої на барабан радіусу r, якщо вантаж масою m, підвішений до намотаної на нього нитки, піднімається із прискоренням а? А) m×g×r. Б) m×(g+a)×r. В) m×(g-а)×r. Г) m×а×r. Д) 2 m×(g+a)×r.
228. Через блок перекинута нитка, на кінець якої прикріплений вантаж масою m =1 кг. Радіус блоку R =10 см. Розрахувати момент сили M, який діє на блок, якщо вантаж опускається на нитці із прискоренням а =2 м/с2. (Вважати g =10 м/с2).
А) 1,6 Н×м. Б) 1,2 Н×м. В) 0,4 Н×м. Г) 2,0 Н×м. Д) 0,8 Н×м.
229. До твердого тіла прикладена сила F =10 Н. Чому дорівнює момент цієї сили М відносно осі, розташованої на відстані r =10 см від точки прикладання цієї сили? Кут a між напрямком радіус-вектора r та напрямком сили F дорівнює 300.
А) 1,25 Н×м. Б) 0,75 Н×м. В) 0,50 Н×м. Г) 0,25 Н×м. Д) 1,50 Н×м.
230. У деякій точці А до твердого тіла прикладена сила F =20 Н. Визначити момент цієї сили М відносно осі, розташованої від точки прикладання сили на відстані r =0,5 м. Кут a між напрямком сили F та напрямком радіус-вектора r дорівнює 600.
А) 5,6 Н×м. Б) 10 Н×м. В) 6,4 Н×м. Г) 8,7 Н×м. Д) 5,0 Н×м.
231. Укажіть правильну форму запису формули для моменту імпульсу i-той точки. А) 232. Яке із приведених співвідношень записане невірно? А) 233. Які із наведених величин визначають момент імпульсу тіла відносно осі z?
А) m, wz. Б) Mz, Iz. В) Iz, wz. Г) Mz, e. Д) Iz, ez.
234. Укажіть розмірність моменту імпульсу: А) 235. Вкажіть необхідну і достатню умову для збереження моменту імпульсу тіла відносно осі z. ( А) 236. У системі виконується закон збереження моменту імпульсу. Як зміниться момент інерції системи І відносно даної осі, якщо її кутова швидкість v збільшиться? А) Зменшиться. Б) Не зміниться. В) Збільшиться. Г). Це залежить від маси тіла. Д) Це залежить від форми тіла.
237. Який із наведених виразів визначає момент імпульсу точки, яка рухається по колу? А) 238. Людина, обертаючись на лаві Жуковського, наближає руки із вантажами до осі обертання. Як при цьому зміняться момент інерції людини I відносно осі обертання, кутова швидкість її обертання v і момент імпульсу L цієї системи? ( - збільшується, ¯ - зменшується).
А) I =const, v , L ¯. Б) I , v , L . В) I ¯, v ¯, L =const. Г) I ¯, v , L =const. Д) I , v ¯, L =const.
239. Людина, обертаючись на лаві Жуковського, розводить руки із вантажами в сторони. Як при цьому зміняться величини моменту інерції I, кутової швидкості w, моменту імпульса L цієї системи? ( - збільшується, ¯ - зменшується). А) I , w , L =const. Б) I , w ¯, L =const. В) I , w ¯, L ¯. Г) I , w ¯, L . Д) I ¯, w , L =const.
240. Фігурист, виконуючи обертання у вовчку, притискає руки до свого торсу. Як зміняться при цьому його момент інерції I відносно осі обертання та кутова швидкість обертання v? ( - збільшується, ¯ - зменшується).
А) I ¯, v . Б) I , v ¯. В) I ¯, v ¯. Г) I , v . Д) I ¯, w =const.
241. Як зміниться момент інерції I і кутова швидкість w маятника Обербека, якщо вантажі перемістити із середини спиць на їхні кінці? ( - збільшується, ¯ - зменшується). А) I , w . Б) I ¯, w . В) I ¯, w ¯. Г) I , w ¯. Д) I , w =const.
242. Однорідний диск масою m =1 кг і радіусом R =20 см рівномірно обертається навколо осі, яка перпендикулярна його площині і проходить через його центр. Лінійна швидкість точок диску на ободі V =1 м/с. Чому дорівнює момент імпульсу диска L відносно цієї осі?
А) 0,25 кг×м2/с. Б) 0,10 кг×м2/с. В) 0,05 кг×м2/с. Г) 0,20 кг×м2/с. Д) 0,15 кг×м2/с.
243. Суцільний циліндр радіусом R =0,1 м із рівномірно розподіленою масою m =0,2 кг, обертається навколо осі, яка співпадає із його твірною, з кутовою швидкістю v =10 рад/с. Визначте момент імпульсу цього циліндра L відносно даної осі.
А) 1×10-2 кг×м2/с. Б) 2×10-2 кг×м2/с. В) 3×10-2 кг×м2/с. Г) 6×10-2 кг×м2/с. Д) 4×10-2 кг×м2/с.
244. Кутова швидкість фігуриста, який обертається у вовчку із щільно притиснутими до грудей руками v1 =3 рад/с. При цьому його момент інерції відносно осі обертання І1 =1,8 кг×м2. Коли фігурист розвів руки в сторони, його кутова швидкість стала v2 =2,7 рад/с. На скільки змінився при цьому момент інерції фігуриста DІ? А) Збільшився на 0,2 кг×м2. Б) Не змінився. В) Зменшився на 0,2 кг×м2. Г) Збільшився на 0,3 кг×м2. Д) Зменшився на 0,3 кг×м2.
245. Яке із наведених співвідношень є виразом основного закону динаміки обертального руху? А) 246. Яка із формул висловлює основний закон динаміки обертального руху? А) 247. На барабан радіусом R =0,1 м намотана нитка, до якої підвішений вантаж. Визначте масу m цього вантажу, щоб при його опусканні із прискоренням а= 2 м/с2, на барабан діяв момент сили М =0,24 Н×м. (Вважати g =10 м/с2).
А) 120 г. Б) 240 г. В) 300 г. Г) 180 г. Д) 360 г.
248. На блок радіусом R =0,2 м намотана нитка, до кінця якої підвішений вантаж масою m =300 г. Чому дорівнює момент інерції блоку I, якщо вантаж, після того, як його відпустили, опускається iз прискоренням a= 3 м/с2. (Вважати g =10 м/с2).
А) 4,2×10-2 кг×м2. Б) 2,8×10-2 кг×м2. В) 5,6×10-2 кг×м2. Г) 6,4×10-2 кг×м2. Д) 2,1×10-2 кг×м2.
249. Суцільний циліндр (диск) радіусом r і масою m котиться без ковзання по горизонтальній площині зі швидкістю V. Які величини досить знати для визначення його повної кінетичної енергії Ek? А) m, V. Б) m, r. В) V, r. Г) m, w. Д) I, v.
250. Суцільний циліндр масою m котиться по горизонтальній поверхні без прослизання зі швидкістю V. Чому дорівнює його повна кінетична енергія Ek? А) 251. Однорідна куля із рівномірно розподіленою масою m котиться без ковзання по горизонтальній площині зі швидкістю V. Чому дорівнює її повна кінетична енергія Ek? А) 252. Порожнистий циліндр (обруч) масою m котиться без ковзання по горизонтальній площині зі швидкістю V. Чому дорівнює повна кінетична енергія обруча Ek, якщо його момент інерції I=mR2?
А) mV2. Б) 0,5mV2. В) 2mV2. Г) 0,75mV2. Д) 0,25mV2.
253. Порожнистий циліндр масою m котиться без ковзання по горизонтальній поверхні зі швидкістю V. Чому дорівнює відношення кінетичної енергії його обертального Еобер та поступального Епост руху?
254. Порожнистий циліндр (обруч) масою m котиться без ковзання по горизонтальній поверхні зі швидкістю V. Чому дорівнює відношення кінетичних енергій його поступального Епост та обертального Еобер руху?
255. Диск масою m котиться без ковзання по горизонтальній поверхні зі швидкістю V. Знайти відношення кінетичних енергій його обертального Еобер та поступального Епост руху.
256. Куля масою m котиться по горизонтальній поверхні без ковзання зі швидкістю V. Визначте відношення кінетичних енергій його обертального Еобер та поступального Епост руху. (Момент інерції кулі I=0,4mR2).
257. Однорідний диск скочується з висоти h по похилій площині. Яку швидкість V він матиме в кінці свого шляху – у основи площини? Силами опору знехтувати. А) V = 258. Порожнистий циліндр (обруч) скочується без прослизання із гладкої похилої площини, висота якої h =0,9 м. Розрахувати його швидкість V у основи похилої площини, якщо спочатку він покоївся. (Вважати g =10 м/с2).
А) 4,2 м/с. Б) 3,0 м/с. В) 2,4 м/с. Г) 3,6 м/с. Д) 1,8 м/с.
259. На яку висоту h підніметься по похилій площині диск, швидкість якого V у її основи була 4 м/с. Вважати диск однорідним, а рух відбувається без прослизання. Тертям знехтувати. (Вважати g =10 м/с2).
А) 0,8 м. Б) 0,4 м. В) 1,6 м. Г) 0,6 м. Д) 1,2 м.
ОСНОВИ ТЕОРІЇ З РОЗДІЛУ “ Робота. Енергія. Закони збереження”
Механічною системою називають сукупність матеріальних точок або тіл, які розглядаються, як єдине ціле. Тіла механічної системи можуть взаємодіяти як між собою, так і з тілами, що не належать даній системі. Сили взаємодії між матеріальними точками (або тілами) механічної системи називають внутрішніми. А сили, з якими на матеріальні точки механічної системи діють зовнішні тіла, називаються зовнішніми. Така механічна система, на яку не діють зовнішні сили, називається замкнутою. Звичайно це модель, але завжди можна припустити, що внутрішні взаємодії тіл системи набагато більші, ніж зовнішні. Для замкнутих систем існують такі функції координат і швидкостей частинок системи, які зберігають в процесі руху постійне значення. Ці функції носять назву інтегралів руху. Адитивних інтегралів руху всього три: це імпульс, момент імпульсу і енергія. Тобто, для замкнутих систем можна ввести закони збереження параметрів стану і руху тіл загальніші, ніж закони Ньютона. У класичній механіці таких законів три: закони збереження імпульсу, моменту імпульсу і енергії. Закони збереження імпульсу і моменту імпульсу відображають властивості симетрії простору – його однорідність і ізотропність – і лежать у основі сучасної механістичної моделі Всесвіту. Однорідність простору полягає у рівноправності всіх його точок, а під ізотропністю простору розуміють рівноправність всіх напрямів у просторі. Розглядаючи механічну систему із n-тіл, маси і швидкості яких дорівнюють m1, m2,…., mn та V1, V2,…., Vn. Після почленного додавання рівнянь руху для
теми тіл зберігається, тобто не змінюється із часом: якщо у одного із тіл замкнутої системи імпульс змінився, то це могло відбутись тільки за рахунок зміни імпульсів інших тіл цієї системи. Основний закон динаміки для обертального руху свідчить, що швидкість зміни моменту імпульсу твердого тіла (системи матеріальних точок) дорівнює результуючому моменту всіх зовнішніх сил. Для замкнутої системи сумарний момент всіх зовнішніх сил, діючих на систему щодо довільної нерухомої осі М =0, тому і dL/dt=0, звідки L=const. Ця рівність виражає закон збереження моменту імпульсу: сумарний момент імпульсу замкнутої системи матеріальних точок зберігається, тобто не змінюється з часом. Нагадаємо, що момент імпульсу твердого тіла щодо нерухомої осі L=I × w, де I – момент інерції тіла щодо цієї осі обертання, w - кутова швидкість його обертання. Закон збереження моменту імпульсу може бути записаний так: I1× w 1= I 2 × w 2. Це означає, що якщо у тіла, яке обертається, унаслідок будь-яких причин відбудеться збільшення моменту інерції, то це приведе до зменшення його кутової швидкості обертання (приклади – обертання фігуриста або акробата). Отже, закони збереження імпульсу і моменту імпульсу обумовлені симетрією простору і виконуються при будь-яких взаємодіях – про що свідчать численні експериментальні дані. Зазначимо, що тривимірність простору визначає векторну природу цих фізичних параметрів. Зміна параметрів p і L визначається тільки зовнішніми силами: зміна положення замкнутої системи у просторі сама по собі не може змінити її стан; така зміна можлива тільки в результаті взаємодії з іншими системами. Таким чином, ці закони справедливі у мега-, макро- і мікросвіті, тому вони називаються великими законами збереження. Ще одним інтегралом руху є енергія. У загальному значенні під енергією розуміється скалярна фізична величина, що є універсальною мірою різних форм руху і взаємодії матерії. Вона відбиває кількісну зміну стану тіла, його рухи або зміну його структури при відповідних взаємодіях. Енергія – це просто число, що розраховується за певними правилами. Як показав А.Ейнштейн, повна енергія системи, що має масу М, визначається співвідношенням: Е=m×с2, де с – швидкість світла у вакуумі. Важливо, що поняття енергії тісно пов'язане із поняттям механічної роботи. Природа нашого Всесвіту така, що в замкнутій ізольованій системі різні форми енергії можуть перетворюватися одна на одну без втрат: іншими словами, при будь-якому фізичному процесі сумарна енергія не змінюється. Це означає, що вона зберігається і в часі, тобто є третім інтегралом руху (після імпульсу і моменту імпульсу). Закон збереження енергії обумовлений просторово-часовою симетрією, і відображає однорідність часу (час скрізь протікає однаково, і фізичні закони інваріантні щодо вибору початку відліку часу). Для енергії суттєвим є те, що абсолютні її значення довільні. Оскільки рух тіл щодо різних систем відліку має відносний характер, то мова іде про зміну параметрів руху. А це означає, що ми розглядаємо лише зміни енергії, тобто вона відносна. В процесі взаємодії тіл, форми руху матерії можуть змінюватись. Зміна виду енергії обумовлена дією на тіло сил і пов'язана із здійсненням роботи. Робота сили – це кількісна характеристика процесу обміну енергією між взаємодіючими тілами. Робота, здійснювана сталою силою F при переміщенні тіла на прямолінійній ділянці
на. Якщо кут a гострий, то cosa>0, і роботу вважають позитивною. Якщо a тупий, то cosa<0, і робота негативна. Якщо a=p/2, то cosa=0 і А=0, тобто сила, діюча перпендикулярно переміщенню тіла роботи не здійснює. Одиниця роботи – Джоуль (Дж): 1 Дж=1 Н×м=1 кг×м2/с2. Якщо сила змінюється як за величиною, так і за напрямом, тіло переміщується по деякій траєкторії. Розглянемо елементарне переміщення dS, на якому діючу силу F можна вважати сталою. Елементарна робота, здійснювана
Фізична величина, що характеризує інтенсивність виконання роботи (робота,
Здатність тіл здійснювати механічну роботу характеризується запасом їх енергії. У механіці розрізняють два види енергії: кінетичну і потенціальну. Кінетична енергія це енергія механічного руху тіла (або системи тіл). Вона визначається роботою, яку може здійснити тіло унаслідок того, що воно володіє певною швидкістю V.
тобто робота дорівнює спаду кінетичної енергії тіла, оскільки вона здійснюється проти зовнішніх сил. Якщо зовнішні сили діють на тіло і здійснюють роботу, то кінетична енергія тіла зростає. Отже, кінетична енергія тіла, рухомого зі швидкістю
Характерні властивостікінетичної енергії: вона завжди позитивна, неоднакова в різних системах відліку, є функцією стану системи. Одиниця енергії – Джоуль (Дж): 1 Дж=1 Н×м=1 кг×м2/с2. Визначимо кінетичну енергію твердого тіла, яке обертається навколо нерухомої
Повна кінетична енергія твердого тіла, яке обертається, дорівнює сумі кінетичних
і обертальний рух одночасно (котиться), то його повна кінетична енергія складаєть-
ну енергію, елементарна робота зовнішніх сил дорівнює приросту його кінетичної
тального руху), а також w×dt=dj, маємо:
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 947; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.224.197 (0.159 с.) |
 Б)
Б) 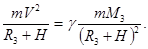 В)
В)  Г)
Г) 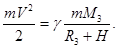 Д)
Д) 
 Б)
Б) 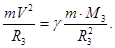 В)
В) 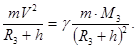 Д)
Д) 
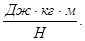
 Б)
Б)  В)
В) 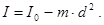 Г)
Г) 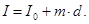 Д)
Д) 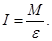
 Б)
Б)  В)
В) 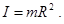 Г)
Г) 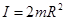 . Д)
. Д) 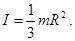
 Б)
Б) 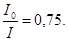 В)
В)  Г)
Г) 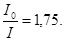 Д)
Д) 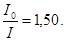
 Б)
Б) 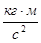 . В)
. В) 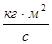 . Г)
. Г)  . Д)
. Д) 
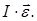 В)
В) 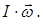 Г)
Г) 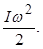 Д) I0+m×d2.
Д) I0+m×d2.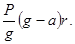 Б) P×r. В)
Б) P×r. В)  Г)
Г) 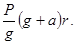 Д)
Д) 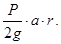
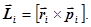 Б)
Б) 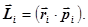 В)
В) 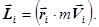 Г)
Г)  . Д)
. Д) 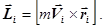
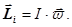 Б)
Б)  В)
В)  Г)
Г) 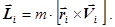 Д)
Д) 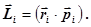
 В)
В) 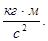 Г)
Г) 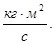 Д)
Д) 
 - сумарний момент всіх зовнішніх сил, прикладених до тіла).
- сумарний момент всіх зовнішніх сил, прикладених до тіла).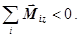 Б)
Б)  В)
В) 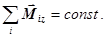 Г)
Г) 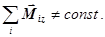 Д)
Д) 
 . Б) mi × ri2. В)
. Б) mi × ri2. В) 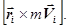 Г) mi × V × t. Д)
Г) mi × V × t. Д) 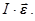
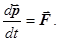 Б)
Б) 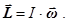 В)
В) 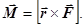 Г)
Г)  Д)
Д) 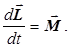
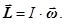 Б)
Б)  Г)
Г)  Д)
Д) 
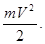 Б)
Б) 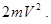 В)
В) 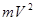 . Г)
. Г) 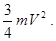 Д)
Д) 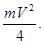
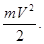 Б)
Б)  В)
В)  Г)
Г)  Д)
Д) 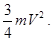
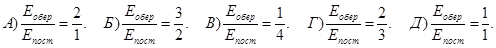


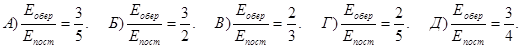
 Б)
Б) 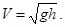 В)
В) 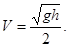 Г)
Г) 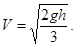 Д)
Д) 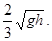
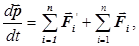
 - сумарний імпульс системи. За третім законом Ньютона, геометрична сума всіх внутрішніх сил механічної системи дорівнює нулю, а в разі замкнутої си-
- сумарний імпульс системи. За третім законом Ньютона, геометрична сума всіх внутрішніх сил механічної системи дорівнює нулю, а в разі замкнутої си-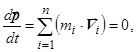 або
або 
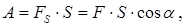
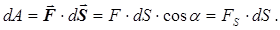
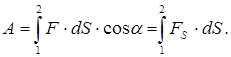
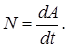
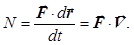
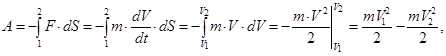
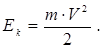
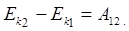
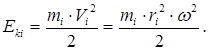
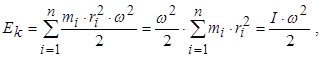
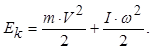
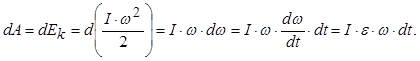
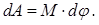 Робота зовнішніх сил при по-
Робота зовнішніх сил при по-


