
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вимоги до оформлення контрольних робіт
1. Семестрові контрольні роботи виконуються чорними або синіми чорнилами чи кульковою ручкою в звичайному шкільному зошиті, на обкладинці якого наводяться відомості студента про себе. Умови задач у контрольній роботі переписуються повністю, без скорочень. Для зауважень та приміток викладача на сторінках зошита потрібно залишати поля. 2. У кінці контрольної роботи вказується, яким підручником чи посібником студент користувався при вивченні фізики та розв'язку задач. Це робиться для того, щоб викладач у випадку необхідності міг вказати, що потрібно студенту вивчити (з цих матеріалів) для закінчення контрольної роботи. У контрольній роботі студент повинен розв'язати задачі того варіанту, номер якого збігається із його шифром. Контрольна робота виконана не за своїм варіантом не перевіряється. 3. Якщо контрольна робота при рецензуванні не зарахована, то студент повинен подати її на повторну рецензію, у яку потрібно включити ті задачі, розв'язки яких були невірними. Повторна робота подається разом із незарахованою. Зарахована контрольна робота подається викладачу на іспит або залік. Студент повинен вміти дати пояснення по суті розв'язку задач, які входять у контрольну роботу. ОСНОВИ ТЕОРІЇ З РОЗДІЛУ “КІНЕМАТИКА МАТЕРІАЛЬНОЇ ТОЧКИ”
Фізика є фундаментом природно-наукової і інженерної освіти, оскільки глибоко впливає на розвиток інших наук і різних галузей техніки. Разом з іншими природними науками фізика вивчає об'єктивні властивості навколишнього нас матеріального світу. Об'єкти навколишнього світу – матеріальні тіла - не залишаються незмінними, а з часом можуть змінювати своє взаємне розташування, форму, розміри, агрегатний стан, фізичні і хімічні властивості і так далі. Всякі зміни, які відбуваються в навколишньому нас світі, є рухом матерії. Рух є спосіб існування матерії. Фізика вивчає найзагальніші форми руху матерії: механічну, теплову, електромагнітну, атомну і ядерну, а також їх взаємні перетворення. Загальною мірою різних форм руху матерії є енергія. Різні фізичні форми руху матерії якісно можуть перетворюватися один на одного, але сама матерія не знищувана і не створювана. Фізика є точною наукою, оскільки вивчає кількісні закономірності явищ. Це експериментальна наука, оскільки багато її законів базуються на фактах, встановлених досвідченим шляхом. Теорії і методи фізики широко використовуються у астрономії, хімії, біології, геології і інших природних науках. Фізичні поняття є простими, і одночасно основоположними і загальними у природознавстві. Це, перш за все, поняття простору, часу, руху, маси, роботи, енергії і багато інших.
Матерія існує у просторі і у часі. Простір і час не існують самі по собі, у відриві від матерії, і матерія не існує поза простором і часом. Простір – об'єктивнареальність, форма існування матерії, що характеризує її протяжність і об'єм, співіснування і взаємодію матеріальних об'єктів і процесів, сукупність відносин координації і розташування об'єктів один щодо одного. Час – поняття, щоописує послідовність зміни явищ і станів матерії, а також їхню відносну тривалість. Разом із простором, час є формою існування матерії: існуєоб'єктивно і пов'язаний із рухом матерії. Найпростішим видом руху матерії є механічний рух, що є зміною взаємного положення тіл або їхніх частин у просторі зі спливанням часу. Розділ фізики, який вивчає механічний рух тіл, називають механікою, яку в свою чергу розділяють на три підрозділи: кінематику, динаміку і статику. Кінематика вивчає рух тіл без урахування причин, що викликають або змінюють його. Динаміка досліджує закони і причини, що викликають рух тіл. Статика розглядає умови рівноваги системи тіл. У свою чергу, механічний рух макроскопічних тіл зі швидкостями, набагато меншими швидкості поширення світла у вакуумі (с =3×108 м/с), вивчає класична (ньютонівська) механіка. У релятивістській механіці (теорії відносності) вивчають механічний рух макроскопічних тіл зі швидкостями, порівнянними зі швидкістю світла у вакуумі. А у квантовій механіці вивчається механічний рух мікроскопічних тіл – окремих атомів і елементарних частинок. У природі не існує ні абсолютного спокою, ні абсолютного руху. Для опису механічного руху даного тіла необхідно вказати будь-яке тіло або систему тіл, які вважаються нерухомими за умов даної задачі, і розглядати рух щодо них. Такі тіла називають тілами відліку. Як правило, із тілом відліку пов'язують систему координат, яка дозволяє встановити положення рухомого тіла у просторі. Простою системою координат є прямокутна декартова система x, у, z. Рух відбувається не тільки у просторі, але і в часі, тому координати тіла при русі змінюються, будучи функціями часу. Для визначення моментів часу, відповідних різним положенням рухомого тіла, необхідно мати годинник, нерухомий щодо тіла відліку, який відлічує проміжки часу відносно довільно вибираного початкового моменту. Системоювідліку називають сукупність тіла відліку, пов'язаної із ним системи координат та годинника для вимірювання часу. Розглядаючи одне і те ж явище в різних системах відліку, ми описуємо його за допомогою тих самих законів, які не змінюються при переході від однієї системи відліку до іншої. Незмінність фізичних законів при переході від однієї системи відліку до іншої носить назву принципу відносності.
При вивченні механічних рухів реальних тіл, зручно абстрагуватись від форми і розмірів тіла, а замінити його на рух однієї точки. Матеріальною точкою називають будь-яке тіло, розмірами якого можна нехтувати за умов даної задачі. (Можливість такого уявлення залежить не від розмірів тіла, а від умов задачі). Будь-яке протяжне тіло можна розглядати, як сукупність (систему) матеріальних точок. Абсолютно твердим тілом називають тіло (систему матеріальних точок), деформацією якого можна нехтувати (відстань між якими не змінюється при його русі). Лінію, яку описує у просторі рухома матеріальна точка, називають траєкторією руху цієї точки. Залежно від типу траєкторії, розрізняють прямолінійний і криволінійний рухи, рух по колу та інші. Траєкторія даного механічного руху в різних системах відліку може мати різну форму. Оскільки фізика є дослідною наукою, уміння спостерігати фізичні процеси і вимірювати різні фізичні величини має особливе значення. Всі зміни, що відбуваються у навколишньому світі зі спливанням часу, оцінюються кількісно за допомогою вимірювань. Виміряти величину означає порівняти її значення із однорідною величиною, прийнятою за одиницю вимірювання. Одиниці фізичних величин можна встановлювати довільно, але для побудови системи одиниць фізичних величин досить вибрати декілька незалежних одна від одної одиниць. Ці одиниці фізичних величин називають основними. Міжнародна система одиниць СІ складається із семи основних одиниць: метр – одиниця довжини, кілограм – маси, секунда – часу, Ампер – сили струму, Кельвін – температури, моль – кількості речовини, кандела – сили світла. Інші одиниці фізичних величин, визначувані через основні, називаються похідними. Скалярні фізичні величини характеризуються тільки своїм чисельним значенням (модулем), а векторні величини окрім чисельного значення характеризуються ще і напрямком. Довільний рух твердого тіла може бути уявлений, як результат накладання поступального і обертального руху. Рух тіла називають поступальним, якщо будь-яка пряма, що єднає дві довільні точки тіла, при його русі залишається паралельною самій собі (всі точки тіла описують паралельні траєкторії однакової довжини). Рух твердого тіла називають обертальним, якщо всі його точки описують кола, центри яких лежать на одній прямій, званій віссю обертання. Положення матеріальної точки А у просторі задається радіусом-вектором r, проведеним із початку системи координат до точки А. При русі точки, її радіус-вектор в загальному випадку змінюється як за модулем, так і за напрямком, тобто він залежить від часу r=r( t ). Цьому векторному рівнянню еквівалентна система скалярних рівнянь: x=x(t), y=y(t), z=z(t). Ці рівняння називають рівняннями руху матеріальної точки.
Розглянемо рух матеріальної точки на ділянці криволінійної траєкторії АВ, почавши відлік часу з моменту, коли точка знаходилась у положенні А. Переміщення точки від А до В за проміжок часу Dt зображається вектором D r. Цей вектор, визначуваний приростом радіус-вектора точки за даний проміжок часу D r=r2-r1, називається вектором переміщення. Довжину ділянки траєкторії АВDS, яку описує матеріальна точка за даний проміжок часу Dt, називають пройденим шляхом. Шлях є скалярною функцією часу DS=DS(t). При прямолінійному русі вектор переміщення співпадає із відповідною ділянкою траєкторії, тому модуль переміщення дорівнює пройденому шляху: úD r ê =DS. Векторна величина, яка визначає як бистроту руху, так і його напрямок у даний момент часу, називається швидкістю руху. Середня швид-
Напрямок вектора середньої швидкості співпадає з напрямком вектора переміщення.
При Dt®0 хорда АВ в межі співпадає із дотичною до траєкторії руху точки, тому вектор миттєвої швидкості спрямований по дотичній до траєкторії у бік її руху. Оскільки модуль вектора переміщення úD r ê для малої ділянки траєкторії співпадає із дов-
Одиниця виміру швидкості – метр в секунду (м/с). Рух тіла із постійною швидкістю (V=const) називають рівномірним. Якщо матеріальна точка скоює плоский рух (при якому всі точки її траєкторії лежать у одній площині), то модуль вектора швидкості визначається формулою: Швидкість руху може змінюватись як за модулем, так і за напрямком. Бистроту зміни швидкості точки характеризують вектором прискорення а. Зміна швидкості на ділянці траєкторії АВ за проміжок часу Dt становить D V=V2-V1, де V1 – швидкість у точці А, а V2 – швидкість у точці В. Середнім прискоренням називається векторна
зміни швидкості D V.Миттєве прискорення у будь-який момент часу (у точці А тра-
похідною швидкості за часом. Одиниця виміру прискорення – метр на секунду в квадраті (м/с2). Вектор зміни швидкості D V можна розікласти на дві складові: D Vt - уздовж дотичної до траєкторії і D Vn – перпендикулярно (по нормалі) до траєкторії. D V t визначає бистроту зміни швидкості по модулю, а D Vn характеризує бистроту змі
мно перпендикулярні складові: тангенціальну аt і нормальну аn. Перша із них співпа-
Нормальна складова прискорення an характеризує зміну швидкості по напрямку і
точки при її криволінійному русі дорівнює геометричній сумі тангенціальної і нор-
Залежно від співвідношення між тангенціальною і нормальною складовими прискорення, класифікують декілька видів руху:
Для визначення шляху, пройденого точкою за проміжок часу від t1 до t2, необхідно знати функціональну залежність її швидкості від часу V(t). Пройдений шлях визначається інтегруванням цієї залежності і чисельно дорівнює площі фігури під
При обертальному русі твердого тіла його точки, що знаходяться на різних відстанях ri від осі обертання, за рівні проміжки часу проходять різні шляхи. Отже, всі вони мають різні швидкості і прискорення. Якщо радіус кола, описуваного деякою точкою, дорівнює r, а її лінійне переміщення (довжина дуги кола) дорівнює dS, то кут повороту радіус-вектора точки (її кутове переміщення) складає dj=dS/r, і є однаковим для всіх точок тіла. Окрім кута повороту, кінематичними характеристиками обертального руху є кутова швидкість w і кутове прискорення e. Якщо тіло за проміжок часу Dt повертається на кут Dj, то швидкість його обертання характеризу-
аксіальним вектором) за правилом правого гвинта: якщо напрям обертання правого гвинта співпадає з обертанням тіла, то вістря гвинта указує напрям вектора кутової швидкості. Якщо w=const, то обертальний рух називають рівномірним. Час одного повного обороту тіла навколо осі обертання називається періодом обертання Т, а величину n, зворотну періоду, - частотою (n=1/Т). Частота обертання визначається кількістю повних оборотів тіла, скоєних ним при рівномірному обертанні за одиницю часу. За час одного періоду кут повороту радіус-вектора точки дорівнює 2p радіан.
віть при постійній по модулю швидкості, такий рух все одно є прискореним, оскільки при V=const напрям швидкості весь час змінюється. Прискорення точки, яка рівномірно рухається по колу, у будь-який момент часу є нормальним (доцентровим), спрямованим по радіусу до центру кола, перпендикулярно вектору швидкості. Бистрота зміни кутової швидкості характеризується кутовим прискоренням. Якщо за проміжок часу Dt кутова швидкість тіла, яке обертається, одержує приріст Dw, то кутовим прискоренням називають векторну величину, визначувана першою
із напрямом вектора кутової швидкості w (визначається за правилом правого гвинта), а при уповільненому обертанні – спрямований протилежно. Одиниця кутового прискорення – радіан в секунду за секунду (рад / с2). Обертання тіла із постійним кутовим прискоренням (e=const)називається рівнозмінним. При такому русі, його кінематичні характеристики зв'язані між собою співвідношеннями, подібними співвід-
тиками поступального і обертального руху можна одержати, використовуючи співвідношення: dS=R×dj, де dS – довжина дуги кола, dj - центральний кут, на який вона спирається, R – її радіус. Диференціювавши це співвідношення за часом, одержуємо зв'язок між лінійною швидкістю V руху точки по колу із кутовою швидкістю
ТЕСТОВІ ЗАВДАННЯ З РОЗДІЛУ “Кінематика МАТЕРІАЛЬНОЇ ТОЧКИ”
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.227.69 (0.03 с.) |



 де Vx=V×cosa, Vy=V×sina - проекції вектора швидкості на осі координат.
де Vx=V×cosa, Vy=V×sina - проекції вектора швидкості на осі координат.






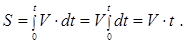






 , або
, або 
 або
або 




