Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення та основні властивості тригонометричних функцій, їх графіки.Стр 1 из 7Следующая ⇒
Означення та основні властивості тригонометричних функцій, їх графіки. Тригонометри́чні фу́нкції — це функції кута. Вони можуть бути визначені як відношення двох сторін та кута трикутника або як відношення координат точок кола.Тригонометричні функції та їхні властивості вивчають на основі таких концентрів.--У курсі геометрії 8 класу вводиться поняття синуса, косинуса і тангенса гострого кута прямокутного трикутника.-- У курсі геометрії 9 класу вивчаються означення синуса, косинуса і тангенса будь-яких кутів від 0° до 180°; теореми синуса і косинуса. Пізніше для будь-яких кутів від 0° до 180° означення цих функцій вводиться координатним способом — за допомогою кола радіуса R у системі координат. Термін «тригонометричні функції» тут не використовується.--У 10 класі в курсі алгебри та початків аналізу повторюються і розширюються відомості про радіанну систему вимірювання кутів і дуг; вводиться поняття кута повороту і розглядаються синус, косинус, тангенс і котангенс довільного гострого кута.Учні вже знають, що sinx, cosx, tgx,ctgx залежать від значень х, отже рівності у=sinx, у=cosx, у=tgx, у=ctgx задають функції, їх називають тригонометричними функціями.
3. Задача 16. Знайти невизначений інтеграл
Абсолютна та умовна збіжність рядів. Ознака Лейбніца збіжності знакозмінного ряду та оцінка його залишку Оз. Знакозмінним наз. ряд, членами якого мають різні знаки. Серед членів знакозмінного ряду є як додатні, так і від’ємні числа, які можуть слідувати в довільному порядку. Найбільш простим є випадок, коли члени ряду по черзі мають то додатний, то від'ємний знак. Знакозмінний ряд зручніше записувати так, щоб знаки членів були позначені, а саме c 1 -c2+c3-c4+... (- 1) n -1 cn+... = де cn> 0 для кожного n. Теор. (Оз. Лейбница). Якщо члени знакозмінного ряду:1) монотонно спадають: cn+1 < cn для кожного n; 2) прямують до нуля: Якщо знакозмінний ряд збігається, а ряд, складений абсолютних величин, розбігається, то знакозмінний ряд називається умовно збіжним.
Теорема. Якщо ряд збігається абсолютно, то ряд, що отримано з нього перестановкою членів, також збігається й має ту ж саму суму, що й початковий ряд. Іншими словами, абсолютно збіжний ряд має переставну властивість. Теорема (Римана). Якщо ряд збігається умовно, то, яке б не було число A, можна так переставити члени ряду, що сума ряду, який отримаємо, буде дорівнювати A.Умовно збіжний ряд переставною властивістю не володіє. Зауваження. Умовна збіжність здійснюється лише завдяки взаємному погашенню додатних і від'ємних членів, і тому істотно залежить від порядку, у якому ці члени йдуть, а абсолютна збіжність заснована на швидкості спадання членів, і від їхнього порядку не залежить. Зауважимо, що сума тільки додатних членів умовно збіжного ряду дорівнює нескінченності, та сума тільки від'ємних членів також дає нескінченність: ∑ а = +∞ ∑ = −∞ ≥0 Внутрішньо предметні та міжпредметні зв’язки Однією з важливих умов міцності знань, умінь і навиків, які формуються в учнів, є здійснення міжпредметних зв’язків в процесі викладання навчальних предметів. Міжпредметні зв’язки – це вираження фактичних зв’язків, що встановлюються в процесі навчання або в свідомості учня, між різними навчальними предметами. Міжпредметні зв’язки мають дві сторони – об’єктивну і суб’єктивну.Об’єктивна сторона міжпредметних зв’язків знаходить вираження в визначенні змісту навчання і враховується при розробці навчальних планів, програм, складанні підручників, навчальних і методичних посібників по відповідних навчальних предметах.Суб’єктивна сторона міжпредметних зв’язків здійснюється викладачами в процесі навчання Класифікація міжпредметних зв’язків: за змістом навчального матеріалу, ·за уміннями, що формуються, ·за методами та засобами навчання ·
В) Моменти інерції
Теорема.
3.? Навчання готових доведень. За умови належної організації навчання готових доведень можна формувати в учнів компоненти самостійного пошуку і побудови доведення. Готові доведення мають виступати як моделі, на яких учні навчаються розумових дій і прийомів розумової діяльності, що покладено в основу вміння доводити, методів доведень та їх застосування, вчаться самостійно шукати доведення за аналогією з вивченим.
Підготовка до навчання учнів доведень здійснюється вже в 5 - 6 класах, де вони ознайомлюються з першими твердженнями і роблять перші кроки у виконанні дедуктивних умовиводів. Цілеспрямоване навчання доведень починається з перших уроків систематичного курсу планіметрії введенням понять «теорема», «доведення теореми». Учні мають вчитися виконувати аналіз формулювання теореми, тобто відокремлювати умову від висновку. Під час вивчення готових складніших доведень (наприклад, ознак рівності трикутників) доцільно запропонувати учням готову таблицю, в якій у лівому стовпчику записано твердження, з яких складається доведення, у правому - відповідні обґрунтування. Демонструючи цю таблицю, потрібно спочатку закрити правий стовпчик і поступово відкривати його в міру того, як учні самостійно знаходитимуть потрібні обґрунтування. Такі таблиці доцільно складати учням після самостійного вивчення окремих найпростіших теорем на уроці за підручником. Під час вивчення готових доведень теорем учні мають усвідомлювати істотні елементи доведення, відсторонюватися від неістотних (розміщення рисунка, позначення літерами) і помічати істотне спільне в доведеннях. Перш ніж проводити докладне доведення, потрібно спочатку назвати основні етапи і твердження, на яких воно ґрунтуватиметься. Досвід показує, що учні краще усвідомлюють і запам'ятовують структуру доведення, якщо записують у символічній формі його короткий виклад. Спочатку треба уважно прослухати доведення за наперед заготовленим на дошці рисунком або за рисунком, який він виконує під час доведення. Після цього вчитель проектує на екран короткий символічний запис умови і вимоги теореми, її доведення, пропонує учням перенести рисунок і записи в зошит, якщо в цьому є потреба. 3. ……… Знайти екстремуми
Обчислити ранг
Вільні коливання струни Означення. Струною називають тверде тіло, довжина якого значно перевищує інші його розміри. Якщо u (x, t) – відхилення від положення рівноваги точки струни з абсцисою x в момент часу t і струна однорідна то рівнянням є
Означення. Рівняння при Хід хвильового процесу залежатиме від його початкового стану та початкових швидкостей. При розгляді задачі про коливання струни додаткові умови можуть бути двох видів: початкові та кінцеві (або крайові). Початкові умови показують, в якому стані перебувала струна в момент початку коливання. Зручніше за все вважати, що струна початку коливатися в момент часу (t = 0). Первинне положення точок струни задається умовою u│t=0= f (x) А початкова швидкість
який задовольняє початкові при
Оскільки початкові умови (задані в точках
Підставляючи загальний розв’язок в крайову умову
Шукаємо нетривіальні розв’язки рівняння (1), які задовольняють крайові умови (3), у вигляді
Підставивши (5) у рівняння (1) і розділивши змінні, одержимо остання рівність можлива тоді і тільки тоді, коли
Підставивши (5) у крайові умови (3), одержимо
Таким чином, нам потрібно знайти ненульові розв’язки рівняння (6) і крайової задачі (7), (8). Задача (7), (.8) не для всяких Задача (7), (8) знаходження власних значень і власних функцій називається задачею Штурма-Ліувілля. Алгоритм методу. 1. Представляємо розв’язок у вигляді 2. Знаходимо власні значення і власні функції задачі Штурма-Ліувілля 3. Для кожноговласного значення 4.Складаємо ряд 5. Невідомі коефіцієнти Розглянемо докладно алгоритм. Шукаємо нетривіальні розв’язки рівняння (1), які задовольняють крайові умови (3), у вигляді
Підставивши (5) у рівняння (1) і розділивши змінні, одержимо остання рівність можлива тоді і тільки тоді, коли
Підставивши (5) у крайові умови (3), одержимо
Таким чином, нам потрібно знайти ненульові розв’язки рівняння (6) і крайової задачі (7), (8). Задача (7), (.8) не для всяких Означення. Ті значення параметра Задача (7), (8) знаходження власних значень і власних функцій називається задачею Штурма-Ліувілля. Знайдемо власні значення та власні функції. Для цього розглянемо окремо випадки, коли а) нехай Підставивши знайдений розв’язок у крайові умови (8), одержимо
при Підставивши його в крайові умови (8), матимемо в) нехай
Задача (7), (8) буде мати нетривіальні розв’язки тільки тоді, коли
Знайденим власним значенням відповідають власні функції Підставивши знайдені власні значення у рівняння (6) і проінтегрувавши його, одержимо
де Розглянемо ряд
Нехай функції
Порівнюючи ряди (12), (13), одержуємо Підставивши знайдені коефіцієнти у (9), одержимо розв’язок задачі (1) - (.3):
Репродуктивний Використовують при поясненні нового матеріалу, перевірки домашнього завдання (учні відтворюють розв'язання задач, формулювання і доведення теорем, означення математичних понять, правила тощо). На уроках, де формуються уміння і навички розв'язування прикладів, задач, застосування репродуктивного методу виявляється в діяльності учнів під час розв'язування вправ і задач за зразком, який дано вчителем або наведено в підручнику, в діяльності за певним алгоритмом. Проблемний виклад як метод навчання математики - полягає в тому, що, пояснюючи навчальний матеріал, учитель сам висуває проблеми і, звичайно, як правило, сам їх розв'язує. Однак постановка проблем посилює увагу учнів, активізує процес сприймання і усвідомлення того, що пояснює вчитель. Частково-пошуковий метод (його інколи називають евристичною бесідою) полягає в тому що вчитель заздалегідь готує систему питань, відповідаючи на які учні самостійно формулюють означення поняття, «відкривають» доведення теореми, знаходять спосіб розв'язування задачі.
Дослідницький метод передбачає самостійний пошук розв'язання пізнавальної задачі. Причому може виявитись потреба, щоб проблему сформулював сам учень або и формулює вчитель, але розв'язують учні самостійно. Суть абстрактно-дедуктивного методу навчання полягає в тому, що під час вивчення нового матеріалу вчитель відразу сам повідомляє означення понять, що вводиться, а потім наводить конкретні приклади об’єктів, що належать до понять. Формулюється и доводиться теорема, і лише після цього розглядаються конкретні приклади застосування нового теоретичного матеріалу. Конкретно-індуктивний метод навчання протилежний абстрактно-дедуктивному методу. Під час навчання цим методом пояснення нового матеріалу починається з розгляду прикладів. Використовуючи приклади, учні мають можливість виділити суттєві ознаки поняття, що вводиться. Це допомагає самостійно чи з допомогою вчителя сформулювати означення поняття. Рисунок до теореми дасть змогу учням виявити властивості зображеної фігури і самостійно чи з допомогою вчителя сформулювати теорему. Програмоване навчання виникло з потреб вдосконалення традиційного навчання і створення кращих умов для реалізації дидактичних принципів навчання. Термін «програмоване навчання» походить від термінів програмування для ЕОМ і здійснюється за навчальними програмами.
Знайти границю функції
Означення та основні властивості тригонометричних функцій, їх графіки. Тригонометри́чні фу́нкції — це функції кута. Вони можуть бути визначені як відношення двох сторін та кута трикутника або як відношення координат точок кола.Тригонометричні функції та їхні властивості вивчають на основі таких концентрів.--У курсі геометрії 8 класу вводиться поняття синуса, косинуса і тангенса гострого кута прямокутного трикутника.-- У курсі геометрії 9 класу вивчаються означення синуса, косинуса і тангенса будь-яких кутів від 0° до 180°; теореми синуса і косинуса. Пізніше для будь-яких кутів від 0° до 180° означення цих функцій вводиться координатним способом — за допомогою кола радіуса R у системі координат. Термін «тригонометричні функції» тут не використовується.--У 10 класі в курсі алгебри та початків аналізу повторюються і розширюються відомості про радіанну систему вимірювання кутів і дуг; вводиться поняття кута повороту і розглядаються синус, косинус, тангенс і котангенс довільного гострого кута.Учні вже знають, що sinx, cosx, tgx,ctgx залежать від значень х, отже рівності у=sinx, у=cosx, у=tgx, у=ctgx задають функції, їх називають тригонометричними функціями.
3. Задача 16. Знайти невизначений інтеграл
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 897; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.31.159 (0.097 с.) |

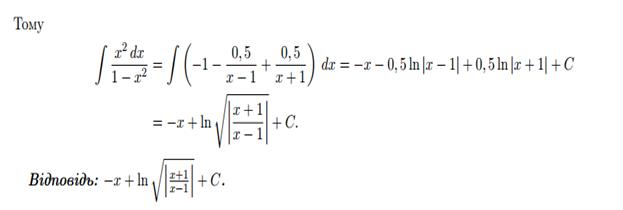 4. Знайти загальний розв’язок рівняння
4. Знайти загальний розв’язок рівняння 

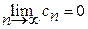 ; то ряд
; то ряд  збігається.
збігається.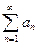 абсолютно збіжний, якщо збігається ряд, утворений із абсолютних величин членів ряду
абсолютно збіжний, якщо збігається ряд, утворений із абсолютних величин членів ряду 
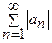 - збігається, то і ряд
- збігається, то і ряд 










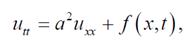
 називають рівняннямвимушених коливань струни. При
називають рівняннямвимушених коливань струни. При  отримуємо рівняння вільних
отримуємо рівняння вільних 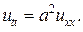 (1)
(1)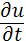 │t=0=
│t=0= 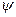 (x) Тобто приходимо до умов
(x) Тобто приходимо до умов  Інший характер мають крайові умови. Вони показують, що відбувається на кінцях струни в увесь час коливань. І простому випадку, коли кінці струни закріплені (початок струни - на початку координат, а кінець - у точці (t, 0)), функції и(х,t) буде підкорятися умовам
Інший характер мають крайові умови. Вони показують, що відбувається на кінцях струни в увесь час коливань. І простому випадку, коли кінці струни закріплені (початок струни - на початку координат, а кінець - у точці (t, 0)), функції и(х,t) буде підкорятися умовам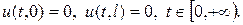 Нехай потрібно знайти розв’язок задачі
Нехай потрібно знайти розв’язок задачі 
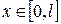 та крайові умови
та крайові умови 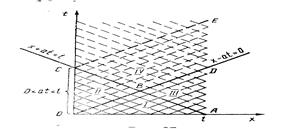 Для побудови розв’язку такої мішаної задачі застосовуємо метод характерис-тик.
Для побудови розв’язку такої мішаної задачі застосовуємо метод характерис-тик.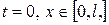 , то розвязок задається дається формулою Д’Аламбера – на рис. область I
, то розвязок задається дається формулою Д’Аламбера – на рис. область I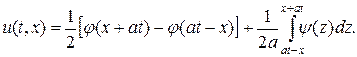
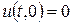 , знаходимо відображену хвилю
, знаходимо відображену хвилю 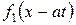 за відомою падаючою хвилею
за відомою падаючою хвилею 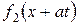 в точках відрізка
в точках відрізка 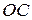 . Це дає можливість побудувати розв’язок розглядуваної мішаної задачі в області II (трикутник
. Це дає можливість побудувати розв’язок розглядуваної мішаної задачі в області II (трикутник 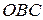 ). Використовуючи другу крайову умову
). Використовуючи другу крайову умову 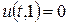 ,знаходимо відображену хвилю
,знаходимо відображену хвилю 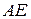 . Це дає можливість знайти шуканий розв’язок в областях III і IV (трикутник
. Це дає можливість знайти шуканий розв’язок в областях III і IV (трикутник 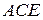 ). Повторюючи вищеприведені міркування, можна побудувати розв’язок мішаної задачі у всій області
). Повторюючи вищеприведені міркування, можна побудувати розв’язок мішаної задачі у всій області  . Розв’язок задачі може бути знайдений і за методом Фурє. Нехай необхідно знайти розв’язок диференціального рівняння
. Розв’язок задачі може бути знайдений і за методом Фурє. Нехай необхідно знайти розв’язок диференціального рівняння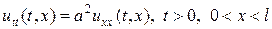 , (1) який задовольняє рівняння
, (1) який задовольняє рівняння 
 (2) і крайові умови
(2) і крайові умови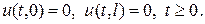 (3)В силу умов узгодженості
(3)В силу умов узгодженості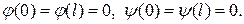 (4)
(4)
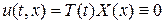 (5)
(5)
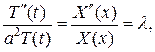
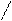
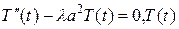 º 0, (6)
º 0, (6)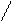

 º 0.(7)
º 0.(7)
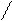 Оскільки
Оскільки 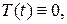 то із останніх рівностей маємо
то із останніх рівностей маємо  (8)
(8)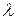 має нетривіальні розв’язки. Означення. Ті значення параметра
має нетривіальні розв’язки. Означення. Ті значення параметра 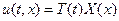 і розв’язуємо задачу Штурма-Ліувілля
і розв’язуємо задачу Штурма-Ліувілля знаходимо загальний розвязок
знаходимо загальний розвязок 
 =
= 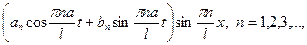
 і
і  , знаходимо, використовуючи початкові умови, отримаємо
, знаходимо, використовуючи початкові умови, отримаємо 

 Тоді загальний розв’язок рівняння (7) має вигляд
Тоді загальний розв’язок рівняння (7) має вигляд 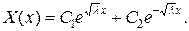
 Визначник системи
Визначник системи 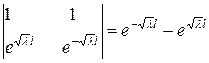
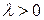 відмінний від нуля, тому система має тільки нульовий розв’язок
відмінний від нуля, тому система має тільки нульовий розв’язок  ,тобто
,тобто  . Таким чином,
. Таким чином,  загальний розв’язок рівняння (7) рівний
загальний розв’язок рівняння (7) рівний  .
. ,
,  . Отже,
. Отже,  і,
і,  . Тоді загальний розв’язок рівняння (7) має вигляд
. Тоді загальний розв’язок рівняння (7) має вигляд

 , а
, а 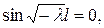 тобто коли
тобто коли ,
, 
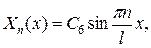 які визначаються з точністю до сталого множника. В зв’язку з цим надалі будемо вважати, що
які визначаються з точністю до сталого множника. В зв’язку з цим надалі будемо вважати, що  .
. Згідно з (5) функції
Згідно з (5) функції
 ,
,  ,задовольняють рівняння (1) і крайові умови (3.3) при довільних
,задовольняють рівняння (1) і крайові умови (3.3) при довільних 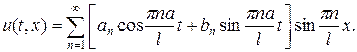 (3.9) Для побудови розв’язку мішаної задачі (1)-.3) залишилось у ряді (9) так вибрати коефіцієнти
(3.9) Для побудови розв’язку мішаної задачі (1)-.3) залишилось у ряді (9) так вибрати коефіцієнти  і
і  є кусково-диференційовними на проміжку
є кусково-диференційовними на проміжку  . Тоді їх можна розкласти в ряди Фур’є
. Тоді їх можна розкласти в ряди Фур’є (13) де
(13) де

 (14)
(14)