Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 5.5 На основании данных таблицы Определите недостающие показатели. Укажите виды относительных величин. Сделайте выводы.Стр 1 из 3Следующая ⇒
Таблица 20– Исходные данные
Задача 6.1 Имеются данные от урожайности пшеницы в районах республики: Таблица 21– Исходные данные
Определите среднюю урожайность пшеницы в отчетном году по республике. Укажите вид средней величины, использованной при решении задач. Сделайте выводы. Задача 6.2 Имеются данные о размерах товарных запасов по магазинам потребительского общества за год: Таблица 22– Исходные данные
Определите средне товарные запасы за год по потребительскому обществу. Укажите вид средней величины, применяемой при расчете. Сделайте выводы. Задача 6.3 Имеются данные о средней скорости автомобилей по маркам: Таблица 23– Исходные данные
Определите среднюю скорость всех автомобилей. Укажите вид средней величины использованной при решении задачи. Сделайте выводы. Задача 6.4 Имеются данные о стоимости основных средств потребительского общества: Таблица 24– Исходные данные
Определите среднюю стоимость основных средств за III, за IV квартал, 2 полугодие. Укажите вид использованных средних величин. Сделайте выводы. Задание 2 Вопросы для самоконтроля:
1. Какие абсолютные величины существует? 2. Какая существует взаимосвязь между относительной величиной выполнения плана, относительной величиной планового задания и относительной величиной динамики? 3. Как определить относительную величину структуры? 4. Что такое средняя величина? 5. Как определяется средняя арифметическая простая и взвешенная? 6. Как определяется средняя гармоническая простая и взвешенная?:
7. Как определяется средняя хронологическая простая и взвешенная? 8. Определение моды? 9. Определение медианы? 10. Какие существуют показатели вариации?
Литература: Егоров Л.И. «Статистика» стр.40-47,66-85 Шмойлова Р.А. «Практикум по теории статистики» стр.100-115,108-112,124-169.
Домашнее задание: подготовиться к проверочному тесту по пройденному материалу.
Практическая работа № 7-8 Тема: « Применение показателей вариации и структурных средних в комплексном анализе социально-экономических явлений и процессов Цель работы: углубить и закрепить теоретические знания по теме «Показатели вариации в статистике. Структурные средние», отработать навыки вычисления, научиться грамотно, анализировать изучаемые социально-экономические явления и процессы с использованием средств вычислительной техники. После изучения темы студент должен: Знать: технику расчета статистических показателей, характеризующих социально-экономические явления; Уметь: осуществлять комплексный анализ изучаемых социально-экономических явлений и процессов с использованием средств вычислительной техники; Ключевые слова и термины: вариация, размах вариации, средняя линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации, мода, медиана; Программа работы: Задание 1 Решите задачи. На оценку «удовлетворительно» 7.1 (пункты а, б) На оценку «хорошо» 7.1 (пункты а, б, в) На оценку «отлично» 7.1 (пункты а, б, в, г) Методические указания к проведению практической работы: Различия индивидуальных значений признака внутри изучаемой совокупности называются вариацией признака. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом отдельном случае. Средняя величина — обобщающая характеристика признака изучаемой совокупности, но она не показывает строение совокупности, не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее. Если отдельные варианты недалеко отстоят от средней, то говорят, что данная средняя хорошо представляет изучаемую совокупность. Для изучения величины отклонений применяют показатели вариации.
При характеристике колеблемости признака применяют систему абсолютных и относительных показателей. К абсолютным показателям вариации относятся 1. Размах вариации:
где 2. Среднее линейное отклонение
3. Дисперсия:
4. Среднее квадратичное отклонение:
Эти показатели (кроме дисперсии) измеряются в тех же единицах, что и сам признак: в тоннах, метрах, секундах, рублях. К относительным показателям вариации относятся: 1. Коэффициент осцилляции: 2. Линейный коэффициент вариации: 3. Коэффициент вариации: Пример Имеются выборочные данные о распределении учителей средних школ по стажу работы. Определить: 1) средний стаж работы учителей; 2) размах вариации; 3) среднее линейное отклонение; 4) дисперсию; 5) среднее квадратическое отклонение; 6) коэффициенты вариации Таблица 25 – Распределение учителей средних школ по стажу работы
Решение. 1. Средний стаж работы учителей; 2.Размах вариации 3.Среднее линейное отклонение 4.Дисперсия 5.Среднее квадратическое отклонение 6.Коэффициент осцилляции: 7. Линейный коэффициент вариации: 8.Коэффициент вариации: Совокупность недостаточно однородна, так как коэффициент осцилляции более 33%. Для характеристики структуры совокупности применяются особые показатели, которые называют структурными средними. К таким показателям относятся мода и медиана. В отличие от средней арифметической и средней гармонической мода и медиана совпадают с конкретным числом, имеющимся в вариационном ряду, и не всегда совпадают со средней арифметической и средней гармонической. Модой {Мо) называется чаще всего встречающийся вариант, или то значение признака, которое соответствует максимальной точке теоретической кривой распределений. В дискретном вариационном ряду мода — это варианта с наибольшей частотой.
4,4; 4,3; 4,4; 4,5; 4,3; 4,3;4,6; 4,2; 4,6; Мо=4,3 тыс. руб. 4,2; 4,3; 4,3; 4,3; 4,4; 4,4; 4,5; 4,6; 4,6; Ме= 4,4
Мо=55руб. Ме=54руб.
Пример. При обследовании 500 семей рабочих одной из отраслей промышленности установлены следующие их размеры по количеству членов семей: Таблица 26Распределение семей по количеству их членов
Определите моду данного вариационного ряда распределения. Решение. Модальной величиной в данном случае будет семья, в составе которой 4 человека, так как этому значению в нашем ряду распределения соответствует наибольшее число семей (260). В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала, то есть того интервала, который имеет наибольшую частоту (частость). В пределах интервала надо найти то значение признака, которое является модой.
Конкретное значение моды для интервального ряда определяется формулой:
Пример. Определить моду продолжительности стажа работы работников торгового предприятия, используя данные таблицы 27. Таблица 27 Распределение работников торгового предприятия по продолжительности стажа работы
Решение. Модальным интервалом величины стажа работников торгового предприятия будет интервал от 6 до 8 лет, так как этот интервал имеет наибольшую частоту (35 человек). Тогда мода продолжительности стажа работы работников торгового предприятия составит:
Наибольшее число рабочих имеют трудовой стаж в размере 6,8 года. Медианой (Me), или серединным вариантом, в статистике называют значение варьирующего признака, который находится в середине ряда значений, расположенных в порядке возрастания или убывания. Для дискретного ранжированного ряда (то есть построенного в порядке возрастания или убывания индивидуальных величин) с нечетным числом членов медианой является варианта, расположенная в центре ряда. Пример Процент выполнения плана товарооборота за месяц 13 торговых предприятий составил (%): 95; 98; 101; 104; 109; 115; 119; 126; 135; 144; 176; 202; 223. Определить медиану. Решение. Медианой здесь будет 7-я варианта, которая делит упорядоченный ряд пополам и соответствует 119 % выполнения плана товарооборота. Для дискретного ранжированного ряда с четным числом членов медианой будет 'варианта, рассчитанная из двух смежных центральных вариант. В интервальном вариационном ряду порядок нахождения медианы следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал. Медианы в интервальном ряду распределения определяется по формуле:
Пример. По данным типового примера 6.7 (табл. 6.5) необходимо рассчитать медиану. Решение. Медианным интервалом величины стажа работников торгового предприятия будет интервал от 6 до 8 лет, так как этот интервал имеет накопленную частоту (82 = 4 + 23 + 20 + 35), которая больше половины всей суммы частот ряда (50 = 100: 2). Тогда медиана продолжительности стажа работы работников торгового предприятия составит:
Более половины рабочих имеют трудовой стаж в размере менее 6,2 года, остальные рабочие более 6,2 года. Задачи для самостоятельного решения: Задача 7.1 Распределение работников фирм по размеру среднемесячной заработной платы характеризуется следующими данными: Таблица 28 Исходные данные.
Вычислите по фирме: 1. Среднемесячную зарплату. 2. Моду и медиану. 3. Размах вариации, среднее линейное отклонение, дисперсию, среднее квадратичное отклонение. 4. Коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации? Задание 2 Вопросы для самоконтроля:
1. Определение моды в вариационном ряду. 2. Определение моды в интервальном ряду 3. Определение медианы в вариационном ряду. 4. Определение медианы в интервальном ряду.? 5. Абсолютные показатели вариации. 6. Относительные показатели вариации
Литература: Егоров Л.И. «Статистика» стр. 66-85 Шмойлова Р.А. «Практикум по теории статистики» стр.100,124-169.
Домашнее задание: подготовиться к проверочному тесту по пройденному материалу. Практическая работа № 9
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1385; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.98.108 (0.064 с.) |
 ,
,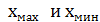 – максимальное и минимальное значение в ряду.
– максимальное и минимальное значение в ряду. , где
, где 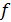 - частота признака;
- частота признака;
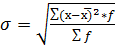



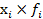



 = 1000/100 = = 10 лет
= 1000/100 = = 10 лет
 = 240/100 = 2.4
= 240/100 = 2.4 =1.55
=1.55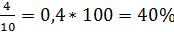


 , где
, где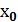 – нижняя граница модального интервала;
– нижняя граница модального интервала; – величина модального интервала;
– величина модального интервала; – частота модального интервала;
– частота модального интервала;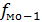 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному; – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.

 – cумма частот;
– cумма частот; – сумма накопленных частот, предшествующих медианному интервалу;
– сумма накопленных частот, предшествующих медианному интервалу; – частота медианного интервала;
– частота медианного интервала;