Прогнозирование (экстраполяция) На основе рядов динамики.

Одна из задач статистики – прогнозирование возможных значений уровней динамического ряда. Эта задача решается на основе статистических методов экстраполяции.

Экстраполяция – приближенный расчет неизвестных уровней динамического ряда, лежащих за его пределами. При осуществлении экстраполяции на основе тренда расчет производится с помощью математического определения по ряду данных значений функций ее значений, находящихся вне этого ряда.

При экстраполяции исходят из предложения, что характер динамики, т.е. та или иная закономерность развития, имевшая место в течении известного периода, сохранится также и в будущем (перспективная экстраполяция - прогнозирование) или имело место в прошлом (ретроперспективная экстраполяция). Важное значение при экстраполяции имеют вопросы о ее базе расчета и сроках прогнозирования. База расчета, определяемая на основе теоретического анализа сущности изучаемого явления, должна быть оптимальной по своей длительности. В качестве такой базы нельзя использовать очень короткий или очень длинный период. При экстраполяции на практике берут те субпериоды базисного ряда динамики, которые составляют определенный этап в развитии изучаемого явления в конкретных исторических условиях. Установление сроков прогнозирования зависит от задачи исследования. Но следует иметь в виду, что чем короче сроки прогнозирования, тем надежнее результат экстраполяции. Обычно рекомендуют, чтобы срок прогноза не превышал одной трети базы расчета.

Применение методов экстраполяции зависит от характера изменений в базисном ряду динамики и предопределяется постановкой задачи исследования. Экстраполяция может производится на основе следующих методов:

1) На основе среднего (постоянного) абсолютного прироста

 

2) на основе среднего (годового, стабильного) темпа роста:

 

3) на основе аналитического выравнивания, когда применяется адекватная трендовая модель;

(например: при выравнивании по прямой объема производства картофеля в районе за 2001-2007гг. была определена на основе функции трендовая модель:

Дл прогнозирования возможного объема производства картофеля в 2010г. модель представляется t=10:

 

 

)

51. абсолютное значение 1% прироста.

Это специфический, самостоятельный, аналитический показатель. Представляет собой отношение абсолютного прироста за какой-либо период времени () к темпу прироста за тот же период, выраженному в процентах

Полученную формулу преобразуют и получаем:

Абсолютное значение 1% прироста широко используется в экономическом анализе, т.к. позволяет ответить на вопрос, какие абсолютные величины скрываются за большими или малыми темпами роста и прироста, т.е. каково абсолютное содержание 1% прироста.

Если известно более двух уровней динамического ряда, то расчет абсолютного значения 1% прироста имеет смысл только для цепных абсолютных приростов и темпов роста по формуле:

Для базисных показателей он будет одним и тем же для всех лет или других периодов времени, т.к. первоначальный уровень (у) остается неизменным.

52.основные примеры и методы обработки и анализа рядов динамики.

Сопоставимость уровней ряда динамики – это сравнимость их (статистических показателей) во времени. охватывает значительные периоды времени, за которые могли произойти изменения, приводящие к причинам несопоставимости. Это:

-изменение территориальных границ областей и т.д.;

(границы москвы и саратова изменились со временем)

- изменение единиц измерения или единиц счета;

(урожай когда то в пудах сейчас в центнерах или тоннах, длина в аршинах теперь в метрах)

- изменение методологии расчета показателей;

(до 1959г. производительность на одного рабочего, после на одного работающего; или же раньше учет урожая по первоначально оприходованному - бункерному весу, а после стали учитывать после доработки-сушки, очистки)

- изменение круга охватываемых объектов;

(ранее обследовалось 62тыс.бюджетов семей рабочих, служащих, колхозников, в современной России – 62 тыс. бюджетов домашних хозяйств)

- разные временные даты;

- сезонные факторы и др.

Вопрос о сопоставимости уровней ряда динамики решается в процессе сбора и обработки данных либо путем их пересчета, например на основе смыкания рядов динамики.

Смыкание – объединение в один ряд двух или нескольких рядов динамики, уровни которой исчислены по разной методологии или разным территориальным границам. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).

Приведение рядов к одному основанию означает определение базисных темпов роста для сравниваемых рядов по отношению к одному и тому же году и их сопоставление.

 

(в этом случае у всех сравниваемых рядов за базу принимается 100%, т.е. приводят к одной базе и сравнивают).

Коэффициент опережения – один из аналитических показателей, используемый в сравнительном анализе нескольких рядов динамики. Дает числовую характеристику процесса опережения за какой-либо период.

если одноименные явления:

1. Коэффициент абсолютного опережения

Показывает, во сколько раз один абсолютный прирост больше другого; должен быть одинаковый период времени и одинаковые знаки (или «+» или «-»)

2. Коэффициент относительного опережения

Показывает, во сколько раз один темп роста больше другого.

Характеризует одинаковый процесс (либо рост, либо снижение)

Аналогично определяются коэффициенты опережения на основе темпов прироста, средних темпов роста и прироста

Если разные явления: используют только относительные показатели динамики (темпы роста и прироста, средние темпа роста и прироста).

Метод скользящей средней – переход от годовых данных к трех четырех и т.д. - летних данных.путем передвижки вперед на один уровень в сглаживании постепенно участвуют все уровни ряда.

Аналитическое выравнивание включает два этапа:1)выбор вида кривой (с помощью графика, на котором фактическим путем выбирается наиболее подходящая кривая; выбранная кривая должна удовлетворять способу наименьших квадратов

)

2)определение параметров функции и выравненных значений уровней ряда

(с помощью системы нормальных уравнений

 

)

Аналитическое выравнивание позволяет не только выявить общее направление основной тенденции, но и дать числовую характеристику изменения динамического ряда в виде показателя средней скорости изменения уровня, что используется при экстраполяции динамических рядов.

 

6. программно – методологические вопросы плана стат. наблюдения.

Объект наблюдения – совокупность явлений, сведения о которых подлежит собрать в процессе наблюдения.

Единица наблюдения – составная часть объекта, его ячейка (семья, предприятие и т.д.)

Программа наблюдения – перечень признаков, который подлежит регистрации у всех единиц наблюдения. правильная программа должна отвечать двум требованиям – полноте и единству.

Полнота определяется включение в неё всех признаков, которые вытекают из цели задач наблюдения. Единство программы означает, что: а) сведения о единицах наблюдения должны быть получены по одной и той же программе, б) понимание и порядок регистрации всех признаков, включенных в программу, едины у всех единиц наблюдения.

Формуляр наблюдения – документ, бланк для регистрации сведений о единицах изучаемой совокупности (переписные листы, формы отчетности и др.)

Различают: карточные формуляры – предназначены для собирания сведений об одной единице наблюдения;

Списочные формуляры – для собирания сведений о двух или нескольких единицах наблюдения.

Способы стат. наблюдения – способ собирания сведений об отдельных единицах наблюдения, которые заносятся в статистический формуляр.

1.непосредственное наблюдение – заполнение соответствующих вопросов формуляра производится непосредственно уполномоченным для этой цели лицом или группой лиц (точный но трудоемкий способ сн)

2. документальный способ – заполнение формуляра на основании соответствующих документов (лежит в основе отчетности, составляемой на основе первичных учетных документов).

Виды опроса:

1) Экспедиционный – устный опрос, непосредственный контакт, наиболее точный из всех разновидностей, но самый неэкономичный.

2) корреспондентский органы наблюдения рассылают по почте единицам наблюдения статистические формуляры с кратким указанием порядка их заполнения. Обратно пересылаются также по почте. Наименее экономичный способ, но наименее точен.

3) саморегистрация – в форме письменного опроса при непосредственном контакте с наблюдаемыми единицами, занимает промежуточное место по точности и экономичности.

Ряды общих индексов

Речь идет о последовательном индексировании общих индексов, т.е. построении системы базисных и цепных общих индексов с постоянными и переменными весами. В зависимости от характера базы и характера весов возможны четыре системы общих индексов.

На примере общего индекса цен по схеме Ласпейреса:

 

 

19.Структурные средние (медиана и мода), способы их расчёта.

Для характеристики структуры вариационных рядов применяются показатели особого рода, которые называют структурными средними.

Мода (Мо) – это значение варьирующего признака, наиболее часто встречающиеся в данном ряду. Модой, или иначе, модальной величиной признака в дискретном ряду является вариант, имеющий наибольшую частоту (или частость).

Медиана (Ме) – это численное значение признака у той единицы изучаемой совокупности, которая находится в середине ранжированного ряда. Медиана делит совокупность на две равные части. Одна часть единиц совокупности имеет значение варьирующего признака меньше, чем медиана, другая – большее.

При определении моды и медианы по данным интервального вариационного ряда применяют специальные формулы:

,

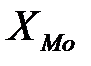где – нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);

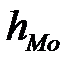– величина модального интервала;

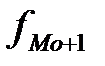, , – частота модального, до и после модального интервалов, соответственно.

,

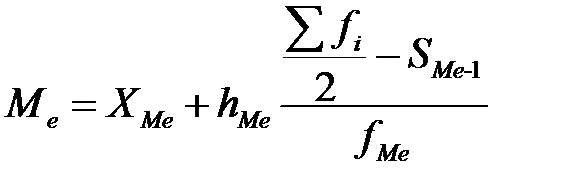где – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);

– величина медианного интервала;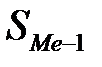

– сумма накопленных частот до медианного интервала;

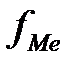– частота медианного интервала.

После расчета медианы и моды необходимо пояснить их экономический смысл.