
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретичні основи електротехнікиСтр 1 из 11Следующая ⇒
ТЕОРЕТИЧНІ ОСНОВИ ЕЛЕКТРОТЕХНІКИ КОНТРОЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ
Міністерство освіти і науки України Вінницький національний технічний університет
ТЕОРЕТИЧНІ ОСНОВИ ЕЛЕКТРОТЕХНІКИ КОНТРОЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ Навчальний посібник
Вінниця ВНТУ
УДК 621.3(075)7 ББК 31.21я73 М13
Автори: В. Г. Мадьяров, І. К. Говор, Ю. Г. Ведміцький, С. Б. Корж
Рекомендовано до видання Вченою радою Вінницького національного технічного університету Міністерства освіти і науки України (протокол №10 від 28 травня 2009 р.)
Рецензенти: П. Д. Лежнюк, доктор технічних наук, професор В. Л. Нагул, кандидат технічних наук В. М. Кутін, доктор технічних наук, професор
Теоретичні основи електротехніки. Контрольні завдання для М13_.самостійної роботи студентів: навчальний посібник /_ _____[Мадьяров_В. Г., Говор І. К., Ведміцький Ю. Г., та ін.] – Вінниця: _____ВНТУ, 2010. – 145 с. В першій частині посібника наведені завдання для розрахунково-графічних робіт, які виконуються студентами самостійно. В другій частині наведені приклади розрахунку електричних кіл. Навчальний посібник призначений для студентів електротехнічних спеціальностей. УДК 621.3(075) ББК 31.21я73
© В. Мадьяров, І. Говор, Ю. Ведміцький, С. Корж, 2010 ЗМІСТ Вступ........................................................................................................ 4 Розрахунково-графічні завдання
1.1_Лінійні кола постійного струму з ідеальними джерелами ЕРС та струму 5 1.2_Лінійні кола постійного струму....................................................... 11 1.3_Лінійні кола однофазного синусоїдного струму............................. 17 1.4_Розрахунок електричного кола синусоїдного струму.................... 23 1.5_Розрахунок несиметричних трифазних кіл..................................... 29 1.6_Ч-1. Лінійні однофазні кола з несинусоїдними ЕРС........................ 40 1.7_Ч-2. Аналіз електричного кола при дії несинусоїдного періо-дичного сигналу.................................................................................................................. 45 1.8_Лінійні трифазні кола з несинусоїдними Е Р С.............................. 49 1.9_Перехідні процеси в лінійних електричних колах.......................... 54 1.10_Перехідні процеси в лінійних електричних колах з подвійною комутацією 60
1.11_Магнітні кола постійного струму................................................... 65 1.12_Комплексна розрахунково-графічна робота №1.......................... 69 1.13_Комплексна розрахунково-графічна робота №2.......................... 77 1.14_Довгі лінії в усталеному режимі..................................................... 83 1.15_Розрахунок електричного поля двох паралельних циліндрів.... 85
Приклади розрахунку електричних кіл 2.1_Методи розрахунку лінійних електричних кіл............................... 87 2.2_Розрахунок лінійних електричних кіл однофазного cтруму.......... 98 2.3_Розрахунок симетричного і несиметричного трифазних кіл.......... 103 2.4_Розрахунок однофазних та трифазних кіл з несинусоїдними ЕРС 114 2.5_Перехідні процеси в лінійних електричних колах.......................... 122 2.6_Розрахунок магнітних кіл постійного струму................................. 127 2.7_Розрахунок довгої лінії.................................................................... 133 2.8_Розрахунок електричного поля двох паралельних циліндрів....... 138 Глосарій................................................................................................... 144 Список літератури................................................................................... 146
Вступ Навчальний посібник написаний відповідно до матеріалу вивчення курсу теоретичних основ електротехніки студентами електротехнічного профілю і є доповненням посібників "Теоретичні основи електротехніки" ч. 1, 2 та 3, що видані кафедрою протягом останніх років. Посібник складається із п’ятнадцяти завдань розрахунково-графічних робіт (РГР), передбачених навчальними планами вивчення дисциплін “Теоретичні основи електротехніки” (бакалаврський напрям 6.050701, 6.050702), “Основи теорії електрорадіокіл” (бакалаврський напрям 6.051004), “Теорія електричних сигналів і кіл” (бакалаврський напрям 6.050201),“Теорія електричних та магнітних кіл” (бакалаврський напрям 6.050101, 6.050102) “Основи електротехніки і електроніки” (бакалаврський напрям 6.050103). Посібник відповідає таким основним розділам теоретичних основ електротехніки як закони Ома та Кірхгофа, методи розрахунку лінійних електричних кіл, кола із взаємоіндукцією, трифазні електричні кола, несинусоїдні струми і напруги в однофазних та трифазних колах (РГЗ №1-8). Розрахунку перехідних процесів відповідають РГЗ № 9,10; РГЗ № 11 –«Магнітні кола постійного струму»; РГЗ № 14 – «Електричні кола з розподіленими параметрами»; РГЗ № 15 – «Теорії електромагнітного кола».
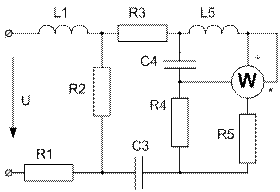
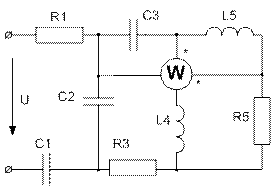
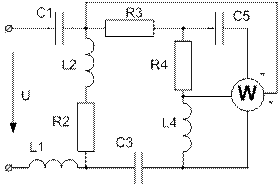
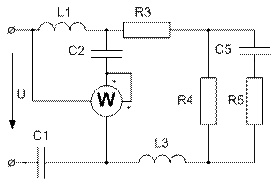
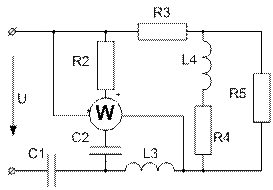
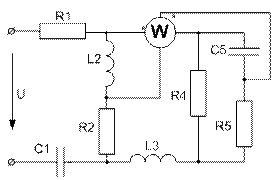
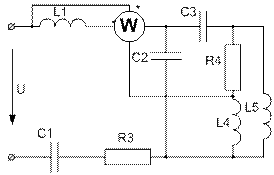
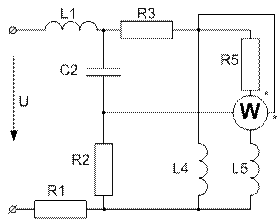
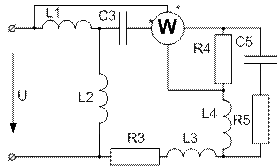
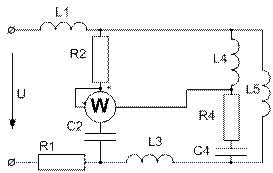
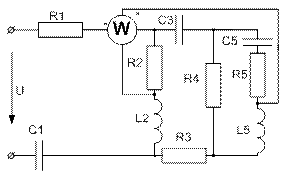
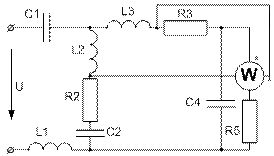
Усі завдання розраховані на широке застосування ЕОМ при їх виконанні. Варіанти завдань визначаються чотиризначним шифром, що видаються викладачем. Дві останніх цифри визначають номер схеми, а дві перших – рядки даних в таблицях 1 і 2 відповідно. Варіанти РГР №15 визначаються за трьома останніми цифрами шифру. В посібнику наведені приклади виконання та оформлення розрахунково-графічних робіт.
Завдання № 1
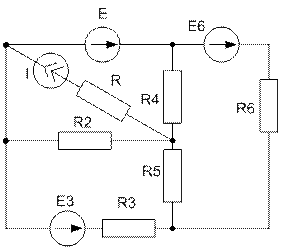
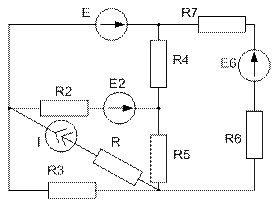
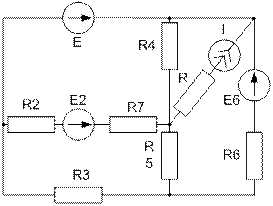
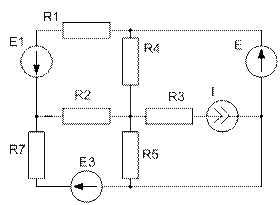
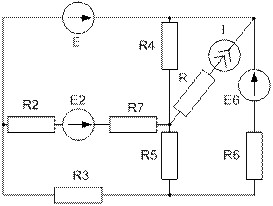
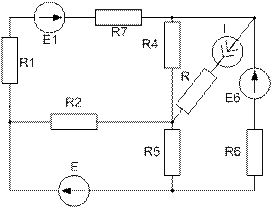
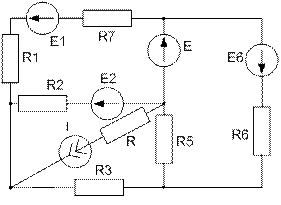
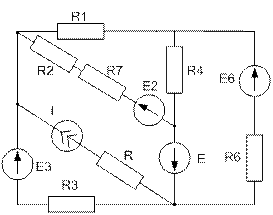
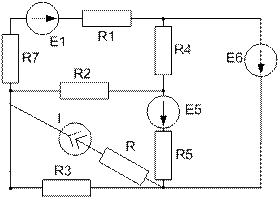
Завдання №2 Лінійні кола постійного струму Для електричного кола, схема якого зображена на рисунку: 1) скласти на підставі законів Кірхгофа систему рівнянь для розрахунку струмів в усіх гілках; 2) визначити струми в усіх гілках методом контурних струмів; 3) визначити струми в усіх гілках методом вузлових потенціалів; 4) визначити струм, показаний на рисунку, методом еквівалентного генератора; 5) результати розрахунку струмів, проведених різними методами, звести в таблицю і порівняти їх; 6) скласти баланс потужностей; 7) накреслити потенціальну діаграму для замкненого контуру, який містить дві ЕРС. Таблиця 1
Таблиця 2
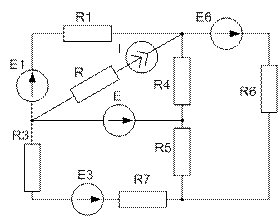
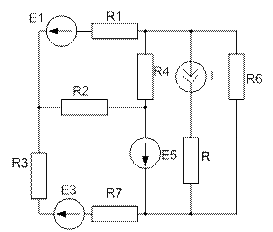
Завдання №3 Таблиця 2
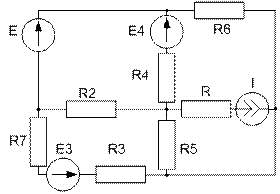
Завдання №4
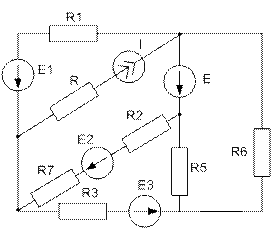
Завдання №5
Завдання № 6 Ч. І
Завдання №7 Ч.ІІ
Аналіз електричного кола Завдання №8
Завдання № 9
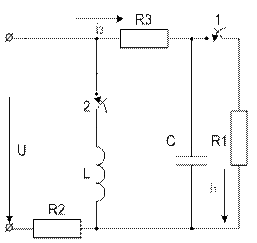
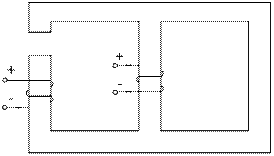
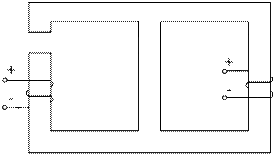
Завдання № 10 З подвійною комутацією Задача 1 Для електричного кола (рисунок 01-24), параметри якого задані в таблицях 1 і 2, спочатку комутує ключ 1, а через час Необхідно розрахувати перехідний процес у колі класичним методом: 1) знайти аналітичні вирази залежності від часу вказаних на рисунках величин; 2) побудувати графіки цих залежностей; 3) визначити практичну тривалість перехідного процесу. Задача 2 Скориставшись результатами, отриманими при виконанні першої задачі за розрахунками кола першого порядку, знайти операторним методом вказані на рисунку величини для кола другого порядку. Примітки: 1) в схемах 05, 11, 14 ключ 2 миттєво переключається з точки a в точку b; 2) в схемах 01, 14, 22 ємності до комутації ключа 1 не заряджені; 3) прикладена напруга в усіх схемах постійна; 4) будувати графіки перехідних величин, починаючи з моменту комутації першого ключа до моменту
Таблиця 1 Таблиця 2
Завдання № 11
Таблиця 1
Таблиця 2
Завдання №12 Завдання №13 Завдання №14 Завдання №15 Метод рівнянь Кірхгофа Перший закон Кірхгофа: алгебраїчна сума струмів у вітках (leg), що сходяться до одного вузла (node) кола, дорівнює нулю. Алгебраїчна сума береться тому, що струми в вітках одного вузла можуть бути по-різному орієнтовані відносно цього вузла. Другий закон Кірхгофа: алгебраїчна сума ЕРС (electromotive force (emf)) будь-якого замкненого контуру (closed circuit) електричного кола дорівнює алгебраїчній сумі спаду напруг (voltage) на елементах цього контуру. Для складання рівнянь за другим законом Кірхгофа необхідно довільно задати напрямок обходу контуру. ЕРС, що входять в рівняння, приймаються додатними, якщо вони збігаються з напрямком обходу контуру. Спади напруг на ділянках кола входять в рівняння зі знаком плюс, якщо напрямок струму (current), що протікає по цій ділянці, збігається з напрямом обходу контуру. Для розрахунку кіл за допомогою рівнянь Кірхгофа необхідно спочатку довільно вибрати напрямки струмів у вітках. При складанні рівнянь за першим законом Кірхгофа струми, які підходять до вузла, беруться зі знаком мінус, направлені від вузла – зі знаком плюс (або навпаки). Число незалежних рівнянь, складених за першим законом, повинно бути на одиницю менше числа вузлів n в схемі.
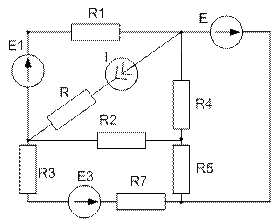
Так, для розрахунку схеми, що містить m віток, треба мати систему m рівнянь, тоді за другим законом Кірхгофа складемо m – (n-1) рівнянь. Отримані таким чином рівняння утворять систему, розв’язування якої дозволяє знайти величину всіх струмів. Якщо при розв’язанні системи будуть від’ємні значення, це означає, що дійсні напрямки струмів не збігаються з довільно вибраними на початку розрахунку. Приклад 2. Скласти рівняння за законами Кірхгофа для схеми (рисунок 2.1), якщо Е1=40 В, Е2=20 В, R1=20 0м, R2=20 0м, R3=40 0м, R4=20 0м, R5=5 0м, R6=50м. Розв’язування. Вибираємо довільно напрямки струмів у вітках, як показано на рисунку 2.5. В схемі три вузли (n=3), тому за першим законом Кірхгофа складаємо (n-1) =2 рівняння. Для вузла a: За другим законом Кірхгофа необхідно скласти m – (n-1) рівнянь, тобто для даної схеми 5 – (3-1) =3 рівняння. При вибраних напрямках обходу контурів
Підставляючи числові значення, одержуємо систему рівнянь:
Метод контурних струмів При розрахунку електричних кіл методом контурних струмів спочатку визначають контурні струми, тобто струми, кожний з яких протікає по власному контуру, залишаючись вздовж нього незмінним (рисунок 2.6). Напрямки контурних струмів вибираються довільно. Струми у вітках визначаються як алгебраїчна сума контурних струмів, що протікають по цих вітках. Так, по вітці, що містить ЕРС Е1 і опір R1, протікає тільки один контурний струм J4, тому струм вітки I1 за величиною дорівнює контурному струму J4. Струми I1 і J4 збігаються за напрямком, тоді I1 = J4 . У вітці, що містить I3 і R3, протікають два контурних струми J1 і J2. Оскільки обидва контурних струми в цій вітці збігаються за напрямком зі струмом вітки I3, тоді I3 = J1+J2. Аналогічно визначаються струми в інших вітках: I2 = J2; I4 = - J1; I3 = - J3 + J4; I6 = J2 - J3; I7 = - J3.
Рівняння для визначення контурних струмів складаються за другим законом Кірхгофа. Контури вибирають таким чином, щоб рівняння, які одержують, були незалежні одне від одного. Для цього необхідно, щоб в кожний новий контур, для якого складається рівняння, входила хоча б одна нова вітка, яка не входила ні в один з раніше розглянутих контурів. При записі рівнянь напрямок обходу контуру звичайно вибирають таким, щоб збігався з напрямком контурного струму; при цьому треба враховувати, що у вітках, які належать двом або більше контурам, протікає відповідна кількість контурних струмів і, отже, спад напруги на таких ділянках складається з алгебраїчної суми спадів напруг від кожного контурного струму. Наприклад, для контуру, в якому протікає струм J 2, рівняння, складене за другим законом Кірхгофа, має вигляд:
Якщо ввести деякі нові позначення і поняття, то запис контурних рівнянь можна формалізувати. В загальному випадку, коли електричне коло містить q контурів, можна записати систему рівнянь:
.................
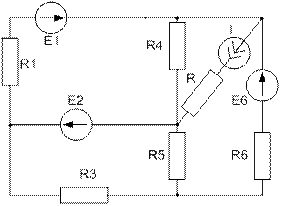
Опір з однаковими індексами ЕРС Приклад 3. Визначити струми у вітках схеми (рисунок 2.7) методом контурних струмів, якщо E1=40 В, E2=40 В, E3=140 В, R1=20 Ом, R2=20_Ом, R3=10 Ом, R4=20 Ом, R5=40 Ом, R6=20 Ом.
Розв’язування. В зв’язку з тим, що електричне коло містить три незалежні контури (independent contour), то систему контурних рівнянь записуємо у вигляді:
Визначимо коефіцієнти отриманої системи рівнянь. Власні опори контурів (own resistance of a contour):
Спільні опори (common resistances):
Враховуючи, що контури 1 і 3 не мають спільної вітки, R13= R31=0. Опір R23 входить в рівняння зі знаком мінус тому, що струми J2 і J3 в цьому опорі направлені в різні сторони. Контурні ЕРС: E11= E3 – E2=100 В; E22= - E1 – E2=-80 В; E33=0. Підставляючи числові значення в систему рівнянь, маємо:
Розв’язавши її, отримуємо: J1 = 4 А; J2 = -3 А; J3 = -2 А. Струми у вітках визначаються із співвідношень: I1 = - J2 = 3 А; I2 = J1 + J2 = 1 А; I3 = J1 = 4 А; I4 = J3 = -2 А; I5 = J3 – J2 = 1 А. Метод вузлових потенціалів Зміст методу полягає в тому, що спочатку визначаються потенціали вузлів (node potential) схеми, а після цього за відомими потенціалами, використовуючи закон Ома для ділянок кола, визначаються струми в вітках. Потенціал одного з вузлів (опорного) можна прийняти рівним нулю, тоді число невідомих в системі вузлових рівнянь буде на одиницю менше числа вузлів. В загальному випадку система вузлових рівнянь для схеми, що містить n+1 вузлів, записується у вигляді:
................
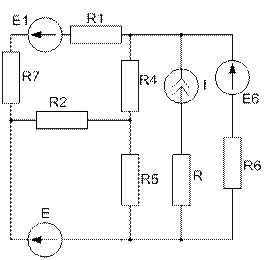
де j n - потенціал n -го вузла; потенціал n+1 -го опорного вузла прийняти рівним нулю; g nn – власна провідність n -го вузла, що визначається як сума провідностей віток, що сходяться в цьому вузлі; g ik – спільна провідність вузлів i та k, дорівнює сумі провідностей віток, що з'єднують безпосередньо вузли i та k. В лінійному колі g ik= g ki; J nn=S E k g k – вузловий струм n -го вузла. Ця величина дорівнює алгебраїчній сумі добутків E k g k, де E k та g k – відповідно ЕРС і провідність віток, що підходять до n -го вузла. Додатне значення цього добутку береться в тому випадку, коли ЕРС E k направлена до даного вузла. Приклад 4. Визначити струми у вітках схеми (рисунок 2.8) методом вузлових потенціалів, якщо E1 = 60 В; E2 = 20 В; E3 = 120 В; R1 = R2 = R4 = = 20 Ом; R3 = R6 = 10 Ом; R5 = 10 Ом. Розв’язування. Приймемо потенціал вузла 3 рівним нулю (j3=0). Запишемо систему двох вузлових рівнянь у загальному вигляді:
Знайдемо коефіцієнти системи. Власна провідність вузла (own conductance of node) 1 складається з чотирьох доданків, бо до нього примикають чотири вітки:
Аналогічно
Спільна провідність (common conductance) вузлів 1 та 2 складається з суми двох доданків, бо ці вузли з'єднані двома вітками:
(Якщо два вузли не з'єднані між собою жодною віткою, то їхня спільна провідність дорівнює нулю). Вузловий струм (node current) першого вузла складається з суми двох доданків, тому що з чотирьох віток, які примикають до нього, лише дві містять ЕРС. Обидві ці ЕРС направлені від вузла 1, тому обидва доданки від’ємні, тобто:
Вузловий струм другого вузла:
Підставляючи числові дані в систему, одержуємо:
Розв'язування системи дасть значення потенціалів: j1 = - 40 В; j2 = 20 В.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 569; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.144.32 (0.168 с.) |








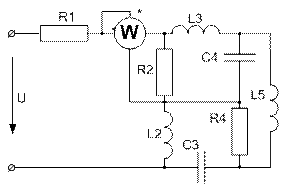
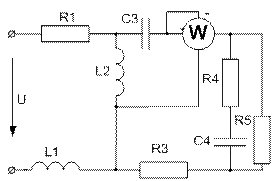
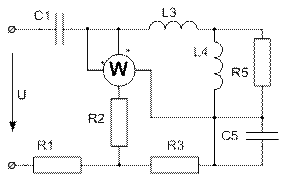
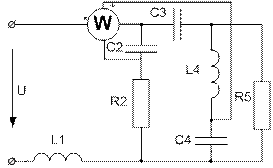




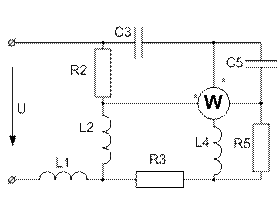
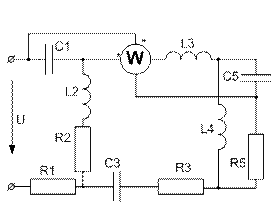
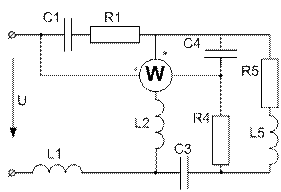
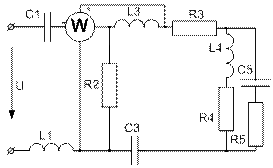
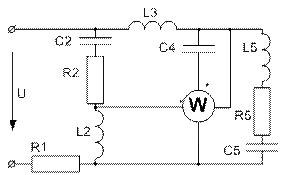
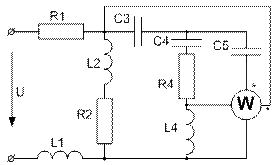
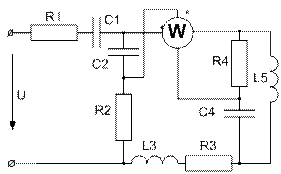
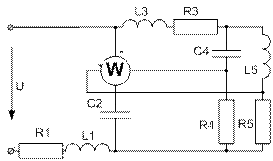
 (
( – стала часу першого порядку) комутує ключ 2.
– стала часу першого порядку) комутує ключ 2. , де
, де  – модуль меншого за абсолютною величиною кореня кола другого порядку.
– модуль меншого за абсолютною величиною кореня кола другого порядку.


































 с
с




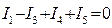 ; для вузла b:
; для вузла b:  .
. ;
; ;
; .
. ;
; ;
;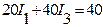 ;
; ;
; .
.


 .
. ;
;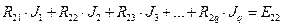 ;
;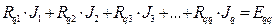 .
. називають власним опором
називають власним опором  -го контуру, оскільки він дорівнює сумі всіх опорів, які належать цьому контуру. Опір з різнойменними індексами
-го контуру, оскільки він дорівнює сумі всіх опорів, які належать цьому контуру. Опір з різнойменними індексами  називається спільним опором контурів
називається спільним опором контурів  і
і  . Якщо ці струми в вітках з опором
. Якщо ці струми в вітках з опором  називають контурною ЕРС. Вона дорівнює алгебраїчній сумі ЕРС, які належать контуру, що розглядається.
називають контурною ЕРС. Вона дорівнює алгебраїчній сумі ЕРС, які належать контуру, що розглядається.
 ;
;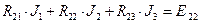 ;
; .
. Ом;
Ом; Ом;
Ом; Ом.
Ом. Ом;
Ом;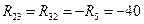 Ом.
Ом. ;
; ;
; .
. ;
;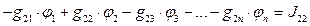 ;
; ,
,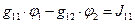 ;
; .
.
 См.
См.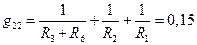 См.
См. См.
См. А.
А.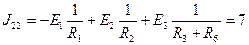 А.
А. ;
; .
.


