
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест Дарбина–Уотсона отсутствия автокорреляции случайного остатка в ЛММР.
Проверка статистической гипотезы Неадекватность этой гипотезы влечет и неадекватность 3й предпосылки теоремы Г-М, что индуцирует негативные для МНК-оценок параметров модели последствия. Шаг 1. По уравнениям наблюдений объекта вычислить МНК-оценки и оценки случайных остатков. Шаг 2. Вычислить статистику Дарбина-Уотсона: Область изменения этой величины: (0,4) Шаг 3. Из таблицы границ интервала критических значений DWпо количеству уравнений наблюдений и количеству объясняющих переменных следует выбрать две величины Шаг 4. Проверить в какое из пяти подмножеств интервала (0,4) попала величина DWи сделать соответствующий вывод.
Тест Д-У базируется на предположении, что 1) Функция регрессии модели является неоднородной (параметр а0 подлежит определению) 2) Случайные остатки в уравнениях наблюдений распределены по нормальному закону 3) Предпосылки 1, 2, 4 теоремы Г-М справедливы
Авторы теста, Дарбин и Уотсон, построили две случайные переменные, такие что:
Т.о. при заданном уровне значимости критерием гипотезы может служить во-первых, множество М1. Во-вторых, множество М5. Т.к.
Величина DWпринимает значения от 0 до 4 так как:
38. Коэффициент детерминации как мерило качества спецификации эконометрической модели (на примере модели Оукена). Скорректированный коэффициент детерминации. Коэффициент детерминации, R2, служит мерой объясняющей способности регрессоров Рассмотрим модель Оукена:
Следовательно, в качестве меры, объясняющей способности регрессора, может служить величина
Она именуется коэффициентом детерминации модели и равно доле эмпирической дисперсии переменной y, которая в рамках обучающей выборки объясняется в модели ее регрессором.
Если При включении в модель новых объясняющих переменных статистика ESS останется на прежнем уровне, либо уменьшится. TSSне изменится.Т.о. увеличивается в ответ на включение в модель дополнительных переменных (необязательно экономически обоснованных). Поэтому в качестве меры объясняющей способности предопределенных переменных модели используют скорректированный на количество регрессоров коэффициент детерминации.
Качество спецификации модели признается удовлетворительным, если регрессоры обладают способностью объяснять значения эндогенной переменной, но наличие такой способности не эквивалентно адекватности модели.
|
|||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 610; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.151.231 (0.007 с.) |
 , приj=i-1 (проверка 3 предпосылки теоремы Г-М)
, приj=i-1 (проверка 3 предпосылки теоремы Г-М)


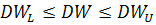 и зависят только от количества уравнений наблюдений количества объясняющих переменных. Т.о. были рассчитаны величины
и зависят только от количества уравнений наблюдений количества объясняющих переменных. Т.о. были рассчитаны величины  , вот их смысл:
, вот их смысл: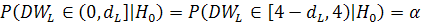


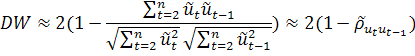
 \\\
\\\ . Это есть объясненная регрессорами в рамках обучающей выборки
. Это есть объясненная регрессорами в рамках обучающей выборки  доля эмпирической дисперсии эндогенной переменной y. Данная величина зависит от выборки и поэтому является случайной переменной, это обстоятельство снижает уровень объективности заключения о качестве спецификации модели, сделанного лишь на основании коэффициента детерминации, чтобы придать большую объективность используетсяяF-тест.
доля эмпирической дисперсии эндогенной переменной y. Данная величина зависит от выборки и поэтому является случайной переменной, это обстоятельство снижает уровень объективности заключения о качестве спецификации модели, сделанного лишь на основании коэффициента детерминации, чтобы придать большую объективность используетсяяF-тест.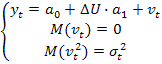 где
где  -темп прироста ВВП,
-темп прироста ВВП,  -изменение уровня безработицы,
-изменение уровня безработицы,  -случайный остаток.Оцененная модель МНК парной регрессии выглядит следующим образом:
-случайный остаток.Оцененная модель МНК парной регрессии выглядит следующим образом: Предполагается, что все предпосылки теоремы Г-М адекватны, обозначим
Предполагается, что все предпосылки теоремы Г-М адекватны, обозначим  как оценку функции регрессии, справедливо
как оценку функции регрессии, справедливо 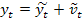 . Первое слагаемое полностью объясняется регрессором, второе, напротив никак им не объясняется, поэтому объясняющая способность регрессора тем выше, чем большую долю в переменной y составляет первое слагаемое. Измерить эту долю можно, если привлечь понятие дисперсии.
. Первое слагаемое полностью объясняется регрессором, второе, напротив никак им не объясняется, поэтому объясняющая способность регрессора тем выше, чем большую долю в переменной y составляет первое слагаемое. Измерить эту долю можно, если привлечь понятие дисперсии.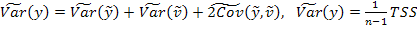 ,
, 


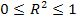
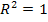 , то значения эндогенной переменной объясняются значениями регрессора (поскольку ESS=0).Напротив, когда
, то значения эндогенной переменной объясняются значениями регрессора (поскольку ESS=0).Напротив, когда 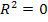 , то спецификация совершенно плоха, т.к. в ее рамах регрессор неспособен объяснять значения эндогенной переменной.Т.е. справедлива гипотеза:
, то спецификация совершенно плоха, т.к. в ее рамах регрессор неспособен объяснять значения эндогенной переменной.Т.е. справедлива гипотеза: 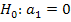 Т.к. коэффициент детерминации вычисляется по выборочным данным, он является случайной переменной, т.е. если
Т.к. коэффициент детерминации вычисляется по выборочным данным, он является случайной переменной, т.е. если  нет полного основания для отклонения гипотезы
нет полного основания для отклонения гипотезы 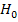 . Для этого используется формализованный критерий F-тест.
. Для этого используется формализованный критерий F-тест.
 . Добавленная в функцию регрессии объясняющая переменная рассматривается как полезная, если в ответ скорректированный коэффициент детерминации увеличился.
. Добавленная в функцию регрессии объясняющая переменная рассматривается как полезная, если в ответ скорректированный коэффициент детерминации увеличился.


