
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Назначение экономико-математических моделей (ЭММ).Стр 1 из 9Следующая ⇒
Назначение экономико-математических моделей (ЭММ). Эконометрика – наука, дающая количественное выражение взаимосвязей экономических явлений и процессов. Базируется на экономической теории, экономической статистике, экономических измерениях, математико-статистическом инструментарии и предназначена для построения эконометрических моделей, которые используются для оценивания и прогнозирования значений экономических переменных, недоступных для измерения. Основная цель: модельное описание конкретных количественных взаимосвязей, обусловленных общими качественными закономерностями, изученными в экономической теории. Экономико-математическая модель объекта – это математически выраженная связь между его экономическими переменными (набор графиков или таблиц), система математических уравнений (или неравенств), связывающая воедино экономические переменные объекта. Говорят, что модель предназначена для объяснения эндогенных (те, которые создаются в модели – «y» короче:)) переменных при помощи экзогенных (наоборот, которые были известны – «х» то бишь) переменных. Задачи: Обнаружение и анализ закономерностей в экономике; построение на базе выявленных закономерностей эконометрических моделей. Два принципа спецификации эконометрических Первый принцип спецификации эконометрической модели заключается в том, что спецификация модели возникает в результате перевода на математический язык экономических утверждений, причем привлекаются, по возможности, линейные алгебраические функции (Или коротко после преобразования модели к математическому языку). Второй принцип требует, чтобы количество уравнений, составляющих спецификацию модели, в точности совпадало с количеством эндогенных переменных, включённых в модель. Типы уравнений в ЭММ: поведенческие уравнения и тождества (на примере макромодели). Экономическим объектом служит закрытая экономика. Ее состояние в текущем периоде t описывается переменными (Yt, Ct, It). Требуется составить спецификацию макромодели, позволяющей объяснять отмеченные выше переменные Вот спецификация: C=a0+a1*Y Y=C+I 0<a1<1
2. Типы переменных в экономических моделях. Структурная и приведённая форма модели (на примере макромодели). Компактная запись.
Лаговые и предопределённые переменные динамической модели. · Предопределенные – текущие и лаговые экзогенные переменные, выступают в роли-факторов-аргументов или объясняющих переменных. · Лаговыми называются экзогенные и эндогенные переменные экономических моделей, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Модели, имеющие лаговые переменные, называются дискретными. Модель Линтнера корректировки размера дивидендов. Пусть pt – текущая прибыль фирмы на акцию после уплаты налогов (в литературе по управлению финансами эта величина традиционно обозначается аббревиатурой EPSt), Dt – дивиденды на акцию, которые фирма выплачивает своим акционерам в текущем периоде (традиционное обозначение DPSt). Известный американский экономист Дж. Линтнер, анализируя дивидендную политику фирм, сформулировал в 1956 г. следующие утверждения: «У фирмы имеется долгосрочная целевая доля γ текущей прибыли и соответствующий этой доле уровень дивидендов Спецификация модели:
Компактная запись. Запишем модель в компактном виде. Для этого введем векторы
соответственно текущих эндогенных переменных и предопределенных переменных модели. Тогда модель предстанет в компактной записи с матрицами:
4. Спецификация и преобразование к приведённой форме эконометрических моделей. Эконометрическая модель Самуэльсона–Хикса делового цикла экономики. Компактная запись. Спецификация и преобразование к приведённой форме эконометрических моделей. Существует 2 принципа спецификации (подробного описания) эконометрических моделей. Первый принцип спецификации эконометрической модели заключается в том, что спецификация модели возникает в результате перевода на математический язык экономических утверждений, причем привлекаются, по возможности, линейные алгебраические функции.
Второй принцип требует, чтобы количество уравнений, составляющих спецификацию модели, в точности совпадало с количеством эндогенных переменных, включённых в модель. Модель, возникающая на этапе спецификации, как правило, имеет структурную форму, отражающую заложенные в модель экономические утверждения. В такой форме эндогенные переменные модели не выражены явно через ее экзогенные переменные. При помощи алгебраических преобразований модель от структурной формы может быть трансформирована к приведённой форме, где каждая эндогенная переменная представляется в виде явной функции только экзогенных переменных модели. Приведённая форма модели непосредственно предназначена для прогноза (объяснения) эндогенных переменных при помощи экзогенных переменных. В частном случае структурная форма модели совпадает с приведённой. Свойства 1. Операции ковариации и корреляции симметричны относительно своих аргументов; 2. Ковариация и корреляция между независимыми переменными равны 0; 3. 4. 5. 6. 7.
12. Случайная переменная и закон её распределения. Закон распределения Фишера. Квантиль, F крит уровня Опр1. Случайная величина Функция Опр2. Случайной называют переменную которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые невозможно заранее учесть. Опр3. Переменная x с областью изменения X называется случайной, если свои возможные значения q из множества X переменная x принимает в результате некоторого опыта со случайными элементарными исходами вида Закон распределения – функция Полной характеристикой СП служит её дифференциальный закон распределения (ЗР). Так называется функция Для дискретной величины Для непрерывной величины Закон распределения Фишера F распределение Плотность Или
Случайная переменная (СП) x именуется дискретной (ДСП), если множество X состоит из конечного или счётного количества констант qi, то есть X = {q1, q2,..., qn }. Если же X есть некоторый интервал числовой прямой, конечный или бесконечный, то есть X = (a, b), то СП x называется непрерывной (НСП). Пусть Случайная переменная
13. Случайный вектор и его основные количественные характеристики (на примере вектора Рассмотрим набор случайных переменных
Его основными характеристиками служат: 1) Вектор ожидаемых значений компонент:
так называют вектор констант, компоненты которого – мат. ожидания компонент вектора 2) Ковариационная матрица:
По главной диагонали располагаются дисперсии компонент случайного вектора. Недиагональные элементы это ковариации компонентов. Например,
ЛММР
Объясняющие переменные
19. Схема Гаусса-Маркова (на примере модели Оукена). Модель Оукена:
t=1,2,... где wt - темп прироста безработицы в году t, yt - темп роста ВВП
Пусть в рамках исследуемой модели величины связаны следующим образом:
Она называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели, или иначе – схемой Гаусса-Маркова ( где
Оценку вектора обозначим где f (·, ·) – символ процедуры. Данная процедура именуется линейной относительно вектора
Понятие статистической процедуры оценивания параметров эконометрической модели. Линейные стат. процедуры. Требования к наилучшей стат. процедуре.
Пусть имеется выборка
значений переменных x и y модели
Данная выборка получена на этапе наблюдения и предназначена для оценивания параметров модели
В рамках данной модели величины (*) связаны следующей СЛАУ:
Она называется системой уравнений наблюдения объекта в рамках исследуемой линейной модели, или иначе – схемой Гаусса-Маркова. Вот компактная запись этой схемы где
Наконец, Оценку вектора обозначим где f (·, ·) – символ процедуры. Данная процедура именуется линейной относительно вектора
Класс таких всевозможных линейных процедур оценивания по исходной выборке вектора Наилучшая процедура f* (·, ·) из выбранного класса процедур F должна генерировать оценку
21. Теорема Гаусса-Маркова – Эйткена. Вывод выражения Теорема (Гаусс, Марков, Эйткен). Пусть матрица X уравнений наблюдений размера n E(u1) = E(u2) =... = E(un) = 0, (1) Var(u1)=..=Var(un)=σ2 (2) Cov(ui,uj)=0, i≠j (3) Cov(xmi,uj) = 0 при всех значениях m=1,…k; i и j. (4) Тогда: a) наилучшая линейная процедура (9.12) имеет вид
б) линейная несмещённая эффективная оценка (9.21) обладает свойством наименьших квадратов
в) ковариационная матрица оценки (9.21) вычисляется по правилу
г) несмещённая оценка параметра s2модели находится по формуле:
где (k+1) – количество неизвестных коэффициентов функции регрессии. Доказательство а. Нам необходимо отыскать процедуру M(X), трансформирующей вектор Из предпосылок (1), (4), а также свойств ковариации следует, что Cov( Также (11) можно представить в виде Или Теперь рассмотрим требование о минимальной дисперсии.
Тогда получим следующую задачу Решив задачу получим Подставим в(9) и получим Теперь сопоставляя (10) и (13) получим
ЧТД
22. Теорема Гаусса-Маркова – Эйткена. Вывод выражения Cov Теорема (Гаусс, Марков, Эйткен). Пусть матрица X уравнений наблюдений размера n E(u1) = E(u2) =... = E(un) = 0, (1) Var(u1)=..=Var(un)=σ2 (2) Cov(ui,uj)=0, i≠j (3) Cov(xmi,uj) = 0 при всех значениях m=1,…k; i и j. (4)
Тогда: a) наилучшая линейная процедура (9.12) имеет вид
б) линейная несмещённая эффективная оценка (9.21) обладает свойством наименьших квадратов
в) ковариационная матрица оценки (9.21) вычисляется по правилу
г) несмещённая оценка параметра s2модели находится по формуле:
где (k+1) – количество неизвестных коэффициентов функции регрессии. Доказательство в. Рассмотрим процедуру Эйткена С учетом Где M = В том случае, когда выполнены (2),(3), то
23. Теорема Гаусса-Маркова – Эйткена. Вывод свойства обобщенного метода наименьших квадратов (ОМНК), Теорема (Гаусс, Марков, Эйткен). Пусть матрица X уравнений наблюдений размера n E(u1) = E(u2) =... = E(un) = 0, (1) Var(u1)=..=Var(un)=σ2 (2) Cov(ui,uj)=0, i≠j (3) Cov(xmi,uj) = 0 при всех значениях m=1,…k; i и j. (4) Тогда: a) наилучшая линейная процедура (9.12) имеет вид
б) линейная несмещённая эффективная оценка (9.21) обладает свойством наименьших квадратов
в) ковариационная матрица оценки (9.21) вычисляется по правилу
г) несмещённая оценка параметра s2модели находится по формуле:
Доказательство. Если вектор случайных возмущений в уравнениях наблюдений имеет произвольную ковариационную матрицу (остатки гетероскедастичны и коррелированны), то оптимальная линейная процедура оценивания параметров линейной модели множественной регрессии именуется обобщённым методом наименьших квадратов (или процедурой Эйткена) и определяется формулами:
M = Обратимся к схеме Гаусса-Маркова и перепишем её по-другому:
На время будем здесь рассматривать вектор
образуем квадратичную (сложную) функцию вектора Нас интересует ответ на вопрос: при каком же значении переменного вектора
Можно проверить, что единственным решением Подставим значение результат подстановки обозначим
В частном случае, когда
так что свойство наименьших квадратов обосновано.
24. Теорема Гаусса-Маркова – Эйткена. Вывод оценки дисперсии единицы веса, Теорема (Гаусс, Марков, Эйткен). Пусть матрица X уравнений наблюдений размера n E(u1) = E(u2) =... = E(un) = 0, (1) Var(u1)=..=Var(un)=σ2 (2) Cov(ui,uj)=0, i≠j (3) Cov(xmi,uj) = 0 при всех значениях m=1,…k; i и j. (4) Тогда: a) наилучшая линейная процедура (9.12) имеет вид
б) линейная несмещённая эффективная оценка (9.21) обладает свойством наименьших квадратов
в) ковариационная матрица оценки (9.21) вычисляется по правилу
г) несмещённая оценка параметра s2модели находится по формуле:
где (k+1) – количество неизвестных коэффициентов функции регрессии. Перепишем схему Гаусса-Маркова в следующем виде: Рассмотрим величину
Получается, что величина
служит несмещённой оценкой константы При условии, что ( для парной регрессии ) Так
(для множественной регрессии аналогично)
Правило ранга. Чтобы сформулировать критерий идентифицируемости i-ro уравнения (1.1), потребуется понятие ограничений на его коэффициенты. Определение 17.1. Ограничениями на коэффициенты i-ro уравнения модели (1.1) называется система из однородных линейных алгебраических уравнений
которым априорно удовлетворяет вектор коэффициентов i-го уравнения модели (1.1). Итак, полагаем, что для i-го поведенческого уравнения модели (1.1) построена матрица Ri ограничений (17.30), состоящая из Li строк и G + К столбцов. Подчеркнем, что Li < G + К. Добавим, что Li — количество переменных модели (1.1), не входящих в i-e уравнение. Обозначим символом
расширенную матрицу ЛМОУ. Матрица (17.36) содержит G строк и G+ К столбцов. Элементами i-й строчки матрицы (17.36) являются компоненты вектора (17.31). Все готово для формулировки критерия идентифицируемости поведенческих уравнений модели (1.1) из линейных одновременных линейных уравнений. Теорема 17.2. В ситуации (1.1) i-е уравнение модели (1.1) из линейных одновременных уравнений идентифицируемо тогда и только тогда, когда справедливо равенство rk( где rk( Доказательство этого важного для эконометрики утверждения, именуемого правилам ранга, предлагается получить в процессе Назначение экономико-математических моделей (ЭММ). Эконометрика – наука, дающая количественное выражение взаимосвязей экономических явлений и процессов. Базируется на экономической теории, экономической статистике, экономических измерениях, математико-статистическом инструментарии и предназначена для построения эконометрических моделей, которые используются для оценивания и прогнозирования значений экономических переменных, недоступных для измерения. Основная цель: модельное описание конкретных количественных взаимосвязей, обусловленных общими качественными закономерностями, изученными в экономической теории. Экономико-математическая модель объекта – это математически выраженная связь между его экономическими переменными (набор графиков или таблиц), система математических уравнений (или неравенств), связывающая воедино экономические переменные объекта. Говорят, что модель предназначена для объяснения эндогенных (те, которые создаются в модели – «y» короче:)) переменных при помощи экзогенных (наоборот, которые были известны – «х» то бишь) переменных. Задачи: Обнаружение и анализ закономерностей в экономике; построение на базе выявленных закономерностей эконометрических моделей. Два принципа спецификации эконометрических Первый принцип спецификации эконометрической модели заключается в том, что спецификация модели возникает в результате перевода на математический язык экономических утверждений, причем привлекаются, по возможности, линейные алгебраические функции (Или коротко после преобразования модели к математическому языку). Второй принцип требует, чтобы количество уравнений, составляющих спецификацию модели, в точности совпадало с количеством эндогенных переменных, включённых в модель. Типы уравнений в ЭММ: поведенческие уравнения и тождества (на примере макромодели). Экономическим объектом служит закрытая экономика. Ее состояние в текущем периоде t описывается переменными (Yt, Ct, It). Требуется составить спецификацию макромодели, позволяющей объяснять отмеченные выше переменные Вот спецификация: C=a0+a1*Y Y=C+I 0<a1<1
2. Типы переменных в экономических моделях. Структурная и приведённая форма модели (на примере макромодели). Компактная запись.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.0.53 (0.157 с.) |
 (желаемый уровень), которые фирма хотела бы выплачивать своим акционерам. Текущий уровень реальных дивидендов, Dt является средневзвешенным значением желаемого объема текущих дивидендов,
(желаемый уровень), которые фирма хотела бы выплачивать своим акционерам. Текущий уровень реальных дивидендов, Dt является средневзвешенным значением желаемого объема текущих дивидендов, 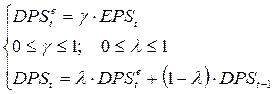
 - время,
- время,  - коэффициент корректировки
- коэффициент корректировки



 ;
; ;
;

 и её расчёт в Excel.
и её расчёт в Excel. называется случайной величиной на вероятностном пространстве
называется случайной величиной на вероятностном пространстве  ,
,  .
. .
. скалярного аргумента q, определенная на всей числовой прямой, характеризующую объективную возможность появления в опыте значений q случайной переменной x.
скалярного аргумента q, определенная на всей числовой прямой, характеризующую объективную возможность появления в опыте значений q случайной переменной x. скалярного аргумента q, определённая на всей числовой прямой, характеризующая объективную возможность появления в опыте
скалярного аргумента q, определённая на всей числовой прямой, характеризующая объективную возможность появления в опыте 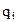 значений СП x. Если x – ДСП, то
значений СП x. Если x – ДСП, то 


 , где
, где  , – независимые случайные величины, распределённые по закону
, – независимые случайные величины, распределённые по закону  со степенями свободы
со степенями свободы  и
и 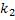 .
.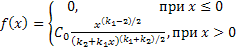 , где
, где 
 (с неотрицательной областью изменения
(с неотрицательной областью изменения 
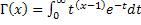 , Г(n+1)=n!, а
, Г(n+1)=n!, а  соответственно натуральные числа (параметры закона Фишера).
соответственно натуральные числа (параметры закона Фишера). - две независимые случайные переменные, имеющие
- две независимые случайные переменные, имеющие  распределение с числом степеней свободы n и m.
распределение с числом степеней свободы n и m. называется дробью Фишера, эта величина распределена по закону Стьюдента. Это позволяет при любом альфа вычислить
называется дробью Фишера, эта величина распределена по закону Стьюдента. Это позволяет при любом альфа вычислить  , удовлетворяющее уравнению
, удовлетворяющее уравнению 
 Это
Это  Эту величины также можно вычислить с помощь Excel, используя функцию FРАСПОБР по аргументам
Эту величины также можно вычислить с помощь Excel, используя функцию FРАСПОБР по аргументам  .
. левых частей схемы Гаусса – Маркова при гомоскедастичном неавтокоррелированном остатке).
левых частей схемы Гаусса – Маркова при гомоскедастичном неавтокоррелированном остатке). . Этот упорядоченный набор называется случайным вектором и обозначается
. Этот упорядоченный набор называется случайным вектором и обозначается 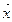 :
: (1)
(1)
 .
. (2)
(2) - это дисперсия компоненты
- это дисперсия компоненты  вектора (1). Элемент
вектора (1). Элемент  - это ковариация компонент
- это ковариация компонент  и
и  вектора (1) Матрица является симметричной.
вектора (1) Матрица является симметричной.
 в общем случае не зависят от случайного остатка
в общем случае не зависят от случайного остатка  . Данная модель является базовой моделью эконометрики, потому что к такому виду может быть трансформирована практически любая эконометрическая модель в виде изолированного уравнения.
. Данная модель является базовой моделью эконометрики, потому что к такому виду может быть трансформирована практически любая эконометрическая модель в виде изолированного уравнения.
 , причём
, причём 
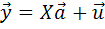 ). Вот компактная запись этой схемы
). Вот компактная запись этой схемы 
 - вектор известных значений эндогенной переменной yt модели;
- вектор известных значений эндогенной переменной yt модели; - вектор неизвестных значений случайных возмущений ut;
- вектор неизвестных значений случайных возмущений ut; - матрица известных значений предопределенной переменной wt модели, расширенная столбцом единиц; наконец,
- матрица известных значений предопределенной переменной wt модели, расширенная столбцом единиц; наконец, – вектор неизвестных коэффициентов уравнения модели.
– вектор неизвестных коэффициентов уравнения модели. . Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим:
. Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим: 
 значений эндогенной переменной yt, если:
значений эндогенной переменной yt, если:  .
. , где матрица коэффициентов, зависящих только от выборочных значений W предопределенной переменной wt
, где матрица коэффициентов, зависящих только от выборочных значений W предопределенной переменной wt



 .
. - вектор известных значений эндогенной переменной yt модели;
- вектор известных значений эндогенной переменной yt модели;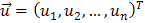 - вектор неизвестных значений случайных возмущений ut;
- вектор неизвестных значений случайных возмущений ut; - матрица известных значений предопределенной переменной x исходной модели, расширенная столбцом единиц (при наличии a0);
- матрица известных значений предопределенной переменной x исходной модели, расширенная столбцом единиц (при наличии a0); – вектор неизвестных коэффициентов уравнения модели.
– вектор неизвестных коэффициентов уравнения модели. . Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим:
. Тот факт, что эта оценка вычисляется по выборочным данным при помощи некоторой статистической процедуры, отразим: 
 значений эндогенной переменной yt, если:
значений эндогенной переменной yt, если:  .
.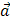 обозначим символом F.
обозначим символом F. , которая обладает одновременно двумя свойствами:
, которая обладает одновременно двумя свойствами: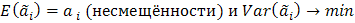 , i=0,1 (эффективности).
, i=0,1 (эффективности). .
. (k+1), где n>(k+1), обладает линейно-независимыми столбцами, а случайные возмущения удовлетворяют 4-м условиям:
(k+1), где n>(k+1), обладает линейно-независимыми столбцами, а случайные возмущения удовлетворяют 4-м условиям: (5)
(5) (6)
(6)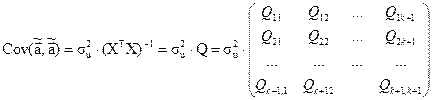 ; (7)
; (7) (8)
(8) в вектор наилучших оценок коэффициентов. Тогда наша задача построить
в вектор наилучших оценок коэффициентов. Тогда наша задача построить  , удовлетворяющим двум условиям оптимальности.
, удовлетворяющим двум условиям оптимальности. 

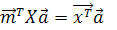
 . (12)
. (12) (из свойства Var(ax+by)=
(из свойства Var(ax+by)=  )
)

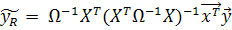 (13)
(13)
 .
.
 и
и  (теорема Фишера),
(теорема Фишера), , получим
, получим  (9)
(9) , тогда (9) превращается в (7)
, тогда (9) превращается в (7)
 . (1)
. (1)  (2)
(2) . (4)
. (4)
 как переменный, тогда вектор
как переменный, тогда вектор  оказывается функцией (аффинным преобразованием) вектора
оказывается функцией (аффинным преобразованием) вектора 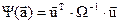 (5)
(5) .
.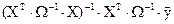 . Это обстоятельство и проясняет причину упомянутого выше названия данной процедуры – обобщённый метод наименьших квадратов.
. Это обстоятельство и проясняет причину упомянутого выше названия данной процедуры – обобщённый метод наименьших квадратов. =
=  , где
, где 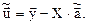 (9.37)
(9.37) , величина
, величина  имеет особенно простой вид:
имеет особенно простой вид: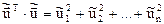 = ESS,
= ESS, .
.

 . Заметим, что при
. Заметим, что при  формула (*) превращается в выражение
формула (*) превращается в выражение  ;
;  ;
;  и с использованием ковариационных правил, можно доказать, что
и с использованием ковариационных правил, можно доказать, что

 (17.30)
(17.30) (17.31)
(17.31) = (А|В) (17.36)
= (А|В) (17.36) ) = G-l, (17.37)
) = G-l, (17.37)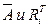 .
.


