
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистичні методи встановлення емпіричних залежностей
При емпіричному (експериментальному) вивченні функціональної залежності величини у від величини х замірюють величину при різних значеннях х. Результати можуть бути представлені у вигляді таблиці 12.3. або графічно. Задача зводиться до аналітичного представлення шуканої функціональної залежності, тобто до підбору формули, яка описує результати експерименту. Особливість задачі полягає в тому, що наявність випадкових похибок зміни ("шуму" в експерименті) робить нерозумним добір такої формули, яка точно відповідала б усім дослідним значенням. Отже, графік шуканої величини не повинен проходити через усі точки, а повинен по можливості згладжувати "шум". Однак, згладжування "шуму" буде більш точним і надійним, чим більше проведено експериментів (тобто чим більше надмірної інформації). Наприклад, для проведення прямої у = ах + b цілком достатньо двох точок (х1,у1) та (х2;у2). Але при наявності більш значного "шуму" для тієї ж мети може знадобитися декілька десятків точок. Таблиця 12.3
Результати експериментів
Емпіричну формулу зазвичай вибирають з формул певного типу (наприклад, у = ах + b, у = аеbх + c). Іншими словами, задача зводиться до визначення параметрів а,b,с,... формули, в той час, як вид формули визначається, виходячи з теоретичних припущень або з міркувань простоти аналітичного уявлення матеріалу. Найбільш простий спосіб переконатися в необхідності підбора для отриманих даних лінійної функції – графічний. Нанесемо дані досвідів на графік, що зручніше за все будувати на міліметровому папері. Дослідні дані, розташовані у виді точок поблизу прямої, будуть свідчити про лінійну функцію. Якщо це так, то лишається лише визначити коефіцієнти а та b. Розглянемо три основних способи визначення коефіцієнтів: натягнутої нитки, середньої і найменших квадратів. Перші два способи дають менш точні результати, однак є більш простими, ніж спосіб найменших квадратів. Спосіб натягнутої нитки полягає у тому, що експериментальні значення наносять на міліметровий папір та проводять пряму, яка найближче всього проходить до цих точок. Вибирають дві довільні точки на прямій (тому спосіб часто називають також способом обраних точок) та визначають їх координати (х1,у1) та (х2;у2). Тоді для визначення коефіцієнтів а та Ь отримають два простих рівняння:
y1 = а1х + b1; y2 = а2х + b2 ( 12.34 ) Спосіб середньої не потребує графічного зображення експериментальних даних і полягає у наступному. Нехай значення, що спостерігалися, наведені у таблиці 12.3. Навіть якщо між x та у теоретично встановлено лінійну залежність y = ах + b. значення у;, які спостерігаються, будуть відрізнятися від ахi+b внаслідок наявності експериментальних похибок. Експериментальна похибка Δi = y1 – axi – b, i = 1,2,…,n. Якщо обирати параметри а та b, так щоб для всіх n спостережень похибки врівноважувалися, тобто
де т – число спостережень у першій групі, яке може бути обрано довільно. Звичайно, т обирають таким чином, щоб число спостережень у другій групі дорівнювало також т, якщо п парне, та т±1, якщо и непарне. Отриману систему для визначення коефіцієнтів а та b записують у наступному вигляді:
Спосіб найменших квадратів полягає у тому, що якщо всі значення функції у1,у2,…,yn виміряні з однаковою точністю, то оцінки параметрів ао,а1,....ап проводять за умови: сума квадратів відхилень значень ук, що заміряні, від розрахункових fN(хк;ао,а1,...аn), тобто:
приймає найменше значення. Вишукування тих значень параметрів ао,а1,...аn, що призводять до найменшого значення функції S = S(ао,а1,...аn), зводиться до рішення системи рівнянь
Аналогічно визначається коефіцієнти для ступеневих функцій виду у = ахb. Такий вид функції зазвичай спостерігається в залежності подовження тканини від прикладеного навантаження. Легко помітити, що функція даного виду зображується у вигляді прямої лінії у логарифмічних осях. Дійсно, після того як проведено логарифмування вказаного рівняння з припущенням, що lgх = Х; lgу= У; lgа = A, можна отримати рівняння
Y = A + bX. (12.39) Для оцінки точності цієї формули необхідно, щоб результати спостережень розміщалися на логарифмічній сітці поблизу прямої лінії. Приклад 7 Необхідно визначити залежність вологості у, % шкіри від часу сушіння х, хв., при температурі 60°С. Об'єм вибірки - шість дослідів. Експериментальні дані представлені нижче.
Визначимо коефіцієнти рівняння у = ах + b. Для цього представимо експериментальні лані у вигляді таблиці 7.2.
Таблиця 12.4
Наведемо основні формули для розрахунку коефіцієнтів:
Використовуючи отримані у табл. 12.4 суми для визначення коефіцієнтів а та b. отримаємо:
Розрахунки можна перевірити за формулою:
У даному випадку маємо 4738 = 814 + 2-720 + 2484, тобто розрахунки виконано вірно. Отримано рівняння: y = 31,43-1,355 x. КОРЕЛЯЦІЙНІ ЗАЛЕЖНОСТІ Залежності між двома величинами, кожна з яких піддається випадковому розсіюванню (неконтрольованому розкидові), вивчають методами кореляційного аналізу. Кореляційний аналіз вивчає усереднений закон поведінки кожної величини в залежності від значень іншої, а також міру залежності між ними. Загальна формула для розрахунку емпіричного коефіцієнту кореляції між величинами xi та уi маєнаступний вигляд:
Зазвичай для спрощення σх та σу розраховують за формулами:
Якщо r<0,25, між уi та xі, то зв'язку між величинами нема. При r=0,25...0,5 між величинами існує дуже слабкий зв'язок, яким можна зневажити, тобто можна вважати, що його практично не існує. Якщо r=0,5....0,7, можна зробити висновок, що між уі та xі існує невеликий зв'язок. При r не менш 0,7 зв'язок вважається добрим, а рівняння регресії досить надійно виражає вплив аргументуй на функцію. Чим ближче | r| до 1, тим тісніше зв'язок між величинами уі та xі..Якщо r приймає додатне значення, характери уі та xі співпадають, при від'ємних значеннях r залежність носить зворотній характер. Ймовірну похибку коефіцієнта кореляції обчислюють за формулою (12.45). Значення ρзалежить від числа визначень п.
У таблиці 12.5 наведено приклад розрахунку коефіцієнту кореляції між абсолютною вологістю W виростка шкіри для одягу хромового дублення з казеїновим покриттям та температурою фазового переходу Т (відповідно х та у ). За отриманими даними розраховуємо коефіцієнт кореляції та ймовірну похибку:
Таблиця 12.5
На основі отриманих даних можна зробити висновок про високий ступень кореляції між абсолютною вологістю шкіри та температурою фазового переходу. ПИТАННЯ ДЛЯ САМОПЕРЕВІРКИ 1. Для чого необхідно проводити математичну обробку результатів
2. Які бувають похибки вимірювань? 3. Що характеризує закон нормального розподілу? 4. Які існують статистичні методи встановлення емпіричних залежностей?
Додаток А Інтеграл Ймовірності
Додаток Б Величини, що пов’язані з інтервалом ймовірності
Додаток В Критичні значення tn(p) для оцінювання значень результатів вимірювань, які «випадають» (n - число прийнятих результатів, p - надійність виводу)
Додаток Г Розподіл Стьюдента [Значення t = t(p;k)]
ДОДАТОК Д
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.219.166 (0.028 с.) |
 то це привело б до отримання одного рівняння, тоді як для находження коефіцієнтів а та b їх необхідно два. Тому припустимо, що врівноваження відбувається не тільки для всіх здійсненних спостережень в цілому, але й для кожної групи, яка містить половину (або майже половину) всіх спостережень окремо. У такому випадку прийдемо до системи рівнянь, яка може бути записана наступним чином:
то це привело б до отримання одного рівняння, тоді як для находження коефіцієнтів а та b їх необхідно два. Тому припустимо, що врівноваження відбувається не тільки для всіх здійсненних спостережень в цілому, але й для кожної групи, яка містить половину (або майже половину) всіх спостережень окремо. У такому випадку прийдемо до системи рівнянь, яка може бути записана наступним чином: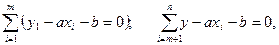 (12.35)
(12.35)
 (12.36)
(12.36) (12.37)
(12.37) (12.38)
(12.38) (12.40)
(12.40) (12.41)
(12.41)
 (12.42)
(12.42)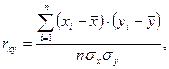 (12.43)
(12.43)
 (12.44)
(12.44) (12.45)
(12.45)



 функція t = t(p) є оберненою до
функція t = t(p) є оберненою до 



