
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сущность, фундаментальные принципы сау и сар.Стр 1 из 11Следующая ⇒
Классификация САУ и САР. Классификация АСР 1 По назначению (по характеру изменения задания): стабилизирующая АСР - система, алгоритм функционирования которой содержит предписание поддерживать регулируемую величину на постоянном значении (x = const); программная АСР - система, алгоритм функционирования которой содержит предписание изменять регулируемую величину в соответствии с заранее заданной функцией (x изменяется программно, например, как функция времени); следящая АСР - система, алгоритм функционирования которой содержит предписание изменять регулируемую величину в зависимости от заранее неизвестной величины на входе АСР (изменяется произвольно). 2 По количеству контуров: одноконтурные - содержащие один контур регулирования (одну обратную связь по регулируемому параметру), многоконтурные - содержащие несколько контуров регулирования (несколько обратных связей, например, по нескольким параметрам, по скорости/ускорению изменения параметра и т.д.). 3 По числу регулируемых величин: одномерные - системы с 1 регулируемой величиной, многомерные - системы с несколькими регулируемыми величинами. Многомерные АСР в свою очередь подразделяются на системы: а) несвязанного регулирования, в которых регуляторы непосредственно не связаны и могут взаимодействовать только через общий для них объект управления; б) связанного регулирования, в которых регуляторы различных параметров одного и того же технологического процесса связаны между собой вне объекта регулирования. 4 По функциональному назначению: АСР температуры, давления, расхода, уровня, напряжения и т.д. 5 По характеру используемых для управления сигналов: непрерывные, дискретные (релейные, импульсные, цифровые). 6 По характеру математических соотношений: линейные, для которых справедлив принцип суперпозиции; нелинейные. Примечание - Если на вход объекта подается несколько входных воздействий, то реакция объекта на сумму входных воздействий равна сумме реакций объекта на каждое воздействие в отдельности: L(х1 + х2) = L(х1) + L(х2), где L - линейная функция (интегрирование, дифференцирование и т.д.). Данный принцип называется принципом суперпозиции (наложения). 7 По виду используемой для регулирования энергии:
пневматические, гидравлические, электрические, механические и др. 8 По наличию внутреннего источника энергии системы прямого действия, системы с вспомогательным источником энергии. 9 По принципу регулирования: по отклонению:
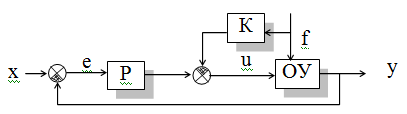
Подавляющее большинство систем построено по принципу обратной связи - регулирования по отклонению. Принцип действия такой системы рассмотрен выше. по возмущению.
Данные системы могут быть использованы в том случае, если есть возможность измерения возмущающего воздействия. На схеме обозначено К - корректирующее звено.
комбинированные - сочетают в себе особенности предыдущих АСР. Данный способ достигает высокого качества управления, поскольку здесь идет коррекция управляющего воздействия не только по величине ошибки, но и по возмущающему воздействию, однако применение данного способа регулирования ограничено тем, что возмущающее воздействие f не всегда возможно измерить.
Основные схемы САР При изображение системы управления (регулирования) применяются два принципа: функциональный и структурный. Функциональная схема – блок-схема системы, заданная функциональным назначением элементов. Структурная схема – блок-схема системы, заданная математическими характеристиками элементов.Структурной схемой САР называется такая схема, все элементы которой представлены своими передаточными функциями. Структурные схемы можно преобразовывать с целью приведения к простейшему (каноническому) виду. Для этого используются следующие правила: 1) последовательное соединение элементов системы, где W(p) = W1(p)·W2(p)
Законы регулирования Программы регулирования По принципу регулирования: по отклонению:
Подавляющее большинство систем построено по принципу обратной связи - регулирования по отклонению (см. рисунок 1.9). Принцип действия такой системы рассмотрен выше. по возмущению.
Данные системы могут быть использованы в том случае, если есть возможность измерения возмущающего воздействия. На схеме обозначено К - корректирующее звено.
комбинированные - сочетают в себе особенности предыдущих АСР.
Данный способ достигает высокого качества управления, поскольку здесь идет коррекция управляющего воздействия не только по величине ошибки, но и по возмущающему воздействию, однако применение данного способа регулирования ограничено тем, что возмущающее воздействие f не всегда возможно измерить.
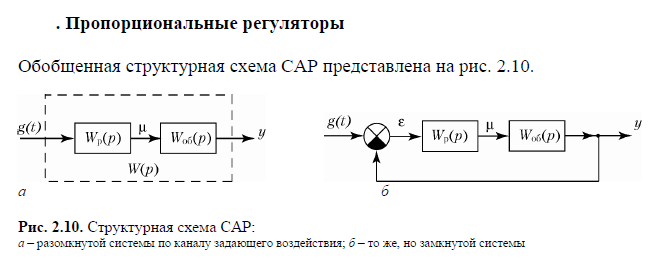
Пропорциональные САР
Для системы регулирования, показанной на рис. 2.10, а, ее амплитудно-фазовая характеристика (АФХ) определяется выражением W (j ω) = W p(j ω) · W об(j ω), (2.5) где W p(j ω) – АФХ регулятора; W об(j ω) – АФХ объекта регулирования. Если комплексная частотная характеристика регулятора будет W p(j ω) = k p, (2.6) то АФХ всей системы запишется в виде W (j ω) = k p · W об(j ω). (2.7) Следовательно, при подключении к объекту регулятора с АФХ (2.6) АФХ системы на каждой частоте увеличивается в k p раз. Такие регуляторы называются пропорциональными (П-регуляторы) и имеют один параметр настройки – коэффициент передачи k p. Переходные процессы в П-регуляторе описываются выражением μ = k p · ε, (2.8) где ε – входное воздействие на регулятор, равное отклонению регулируемой величины от заданного значения; μ – воздействие регулятора на объект, направленное на ликвидацию отклонения регулируемой величины от заданного значения. Комбинированные САР используют оба принципа. а) с воздействием по отклонению регулируемого параметра (принцип Ползунова); б) с воздействием по возмущению, т. е. по изменению нагрузки (принцип Понселе); По свойствам в установившемся режиме различают статические и астатические САР. Статической называют систему, в которой регулируемый параметр в различных установившихся режимах может принимать различные значения. Остаточную ошибку в такой системе называют статизмом. Астатической называют систему, в которой регулируемый параметр в различных установившихся режимах принимает одно и то же значение независимо от величины возмущающего воздействия на объект регулирования. Статизм такой системы всегда равен нулю.
Примеры типовых звеньев Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую природу (электрические, пневматические, механические и др. звенья), но описываться одинаковыми ДУ, а соотношение входных и выходных сигналов в звеньях описываться одинаковыми передаточными функциями. В ТАУ выделяют группу простейших звеньев, которые принято называть типовыми. Статические и динамические характеристики типовых звеньев изучены достаточно полно. Типовые звенья широко используются при определении динамических характеристик объектов управления. Например, зная переходную характеристику, построенную с помощью самопишущего прибора, часто можно определить, к какому типу звеньев относится объект управления, а следовательно, его передаточную функцию, дифференциальное уравнение и т.д., т.е. модель объекта. Типовые звенья Любое сложное звено может быть представлено как соединение простейших звеньев. К простейшим типовым звеньям относятся: · усилительное, · инерционное (апериодическое 1-го порядка), · интегрирующие (реальное и идеальное),
· дифференцирующие (реальное и идеальное), · апериодическое 2-го порядка, · колебательное, · запаздывающее. 1) Усилительное звено.
Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз. у = K.x. При ступенчатом воздействии h(t) = K. Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др. 2) Интегрирующее. 2.1) Идеальное интегрирующее. Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины:
При подаче на вход звена ступенчатого воздействия x(t) = 1 выходной сигнал постоянно возрастает: h(t) = K.t. Это звено астатическое, т.е. не имеет установившегося режима. Примером такого звена может служить емкость, наполняемая жидкостью. Входной параметр – расход поступающей жидкости, выходной - уровень. Изначально емкость пуста и при отсутствии расхода уровень равен нулю, но если включить подачу жидкости, уровень начинает равномерно увеличиваться. 2.2) Реальное интегрирующее.
Передаточная функция этого звена имеет вид: W(s) = Переходная характеристика в отличие от идеального звена является кривой h(t) = K.(t – T) + K.T.e-t/T.
Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора. Если напряжение на двигатель не подается, то ротор не двигается и угол его поворота можно принять равным нулю. При подаче напряжения ротор начинает раскручиваться, а угол его поворота сначала медленно вследствие инерции, а затем быстрее увеличиваться до достижения определенной скорости вращения. 3) Дифференцирующее. 3.1) Идеальное дифференцирующее. Выходная величина пропорциональна производной по времени от входной:
При ступенчатом входном сигнале выходной сигнал представляет собой импульс (d-функцию): h(t) = K.d(t). 3.2) Реальное дифференцирующее.
Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям, передаточные функциикоторыхимеют вид: W(s) = Переходная характеристика: Пример звена: электрогенератор. Входной параметр – угол поворота ротора, выходной – напряжение. Если ротор повернуть на некоторый угол, то на клеммах появится напряжение, но если ротор далее не вращать, напряжение снизится до нуля. Резко упасть оно не может вследствие наличия индуктивности у обмотки.
4) Апериодическое (инерционное). Этому звену соответствуют ДУ и ПФ вида: Определим характер изменения выходной величины этого звена при подаче на вход ступенчатого воздействия величины х0. Изображение ступенчатого воздействия: X(s) = Разложим дробь на простые:
Оригинал первой дроби по таблице: L-1{ Тогда окончательно получаем: y(t) = Kx0 (1 - Постоянная Т называется постоянной времени. Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону. 5) Звенья второго порядка
Звенья имеют ДУ и ПФ вида
W(s) = При подаче на вход ступенчатого воздействия амплитудой х0 переходная кривая будет иметь один из двух видов: апериодический (при Т1³ 2Т2) или колебательный (при Т1 < 2Т2).
В связи с этим выделяют звенья второго порядка: · апериодическое 2-го порядка (Т1³ 2Т2), · инерционное (Т1 < 2Т2), · консервативное (Т1= 0). 6) Запаздывающее. Если при подаче на вход объекта некоторого сигнала он реагирует на этот сигнал не моментально, а спустя некоторое время, то говорят, что объект обладает запаздыванием. Запаздывание – это интервал времени от момента изменения входного сигнала до начала изменения выходного. Запаздывающее звено – это звено, у которого выходная величина у в точности повторяет входную величину х с некоторым запаздыванием t: y(t) = x(t - t). Передаточная функция звена: W(s) = e-ts. Примеры запаздываний: движение жидкости по трубопроводу (сколько жидкости было закачано в начале трубопровода, столько ее выйдет в конце, но через некоторое время, пока жидкость движется по трубе), движение груза по конвейеру (запаздывание определяется длиной конвейера и скоростью движения ленты) и т.д.
Усилительное звено.
Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления. Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз. у = K.x. При ступенчатом воздействии h(t) = K. Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др.
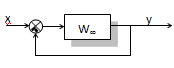
Структурные схемы. Для исследования и расчета структурную схему АСР путем эквивалентных преобразований приводят к простейшему стандартному виду «объект - регулятор». Практически все инженерные методы расчета и определения параметров настройки регуляторов применены для такой стандартной структуры. В общем случае любая одномерная АСР с главной обратной связью путем постепенного укрупнения звеньев может быть приведена к такому виду.
Если выход системы у не подавать на ее вход, то получается разомкнутая система регулирования, передаточная функция которой определяется как произведение: W¥ = Wp.Wy (Wp - ПФ регулятора, Wy - ПФ объекта управления).
То есть последовательность звеньев Wpи Wy может быть заменена одним звеном с W¥. Передаточную функцию замкнутой системы принято обозначать как Ф(s). Она может быть выражена через W¥: Фз(s) = (далее будем рассматривать только системы с обратной отрицательной связью, поскольку они используются в подавляющем большинстве АСР). Данная передаточная функция Фз(s) определяет зависимость у от х и называется передаточной функцией замкнутой системы по каналу задающего воздействия (по заданию). Для АСР существуют также передаточные функции по другим каналам: Фe(s) = Фв(s) = где Wу.в.(s) – передаточная функция объекта управления по каналу передачи возмущающего воздействия. В отношении учета возмущения возможны два варианта: - возмущение оказывает аддитивное влияние на управляющее воздействие; - возмущение влияет на измерения регулируемого параметра. Примером первого варианта может быть влияние колебаний напряжения в сети на напряжение, подаваемое регулятором на нагревательный элемент объекта. Пример второго варианта: погрешности при измерениях регулируемого параметра вследствие изменения температуры окружающей среды. Wу.в.–модель влияния окружающей среды на измерения.
Для первого варианта передаточная функция Wу.в. принимается равной Wу, для второго – как правило, на схеме она выделена в отдельное звено. Поскольку передаточная функция разомкнутой системы является в общем случае дробно-рациональной функцией вида W¥ = Фз(s) = Фe(s) = гдеD = A + B. Как видно, эти передаточные функции отличаются только выражениями числителей. Выражение знаменателя называется характеристическим выражением замкнутой системы и обозначается как Dз(s) = A(s) + B(s), в то время как выражение, находящееся в знаменателе передаточной функции разомкнутой системы W¥, называется характеристическим выражением разомкнутой системы А(s). Пример. Определение передаточных функций АСР. Структура АСР представлена на рисунке. Требуется определить передаточные функции регулятора, объекта, разомкнутой системы, замкнутой системы и характеристические выражения.
ПараметрыK0 = 1, K1 = 3, K2 = 1,5,K4 = 2, K5 = 0,5. В структурной схеме АСР звенья, соответствующие регулирующему устройству, стоят перед звеньями объекта управления и генерируют управляющее воздействие на объект u. По схеме видно, что к схеме регулятора относятся звенья 1, 2 и 3, а к схеме объекта – звенья 4 и 5. Учитывая, что звенья 1, 2 и 3 соединены параллельно, получаем передаточную функцию регулятора как сумму передаточных функций звеньев:
Звенья 4 и 5 соединены последовательно, поэтому передаточная функция объекта управления определяется как произведение передаточных функций звеньев:
Передаточная функция разомкнутой системы:
откуда видно, что числитель В(s) = 1,5.s2 + 3.s + 1, знаменатель (он же характеристический полином разомкнутой системы) А(s) = 2.s3 + 3.s2 + s. Тогда характеристический полином замкнутой системы равен: D(s) = A(s) + B(s) = 2.s3 + 3.s2 + s + 1,5.s2 + 3.s + 1 = 2.s3 + 4,5.s2 + 4.s + 1. Передаточные функции замкнутой системы: по заданию по ошибке При определении передаточной функции по возмущению принимается Wу.в. = Wоу. Тогда
Колебательное звено Амплитудно-фазовая частотная характеристика (АФХ) имеет вид и определяется соотношением
Амплитудно-частотные характеристики (АЧХ) для различных значений x имеет вид (рис. 22б) и определяется соотношением
Фазовая частотная характеристика (ФЧХ) имеет вид и определяется соотношением
Частотные характеристики колебательного звена имеют вид
Пример. Передаточная функция неизменяемой части САР:
– действительная часть:
– мнимая часть:
Амплитудно-частотная характеристика описывается выражением:
. Рисунок 2 - Амплитудно-частотная характеристика
Фазовая частотная характеристика описывается выражением:
Рисунок 3 - Фазовая частотная характеристика
ЧХ систем с обратной связью Обратная связь может быть как положительной, так и отрицательной. Отрицательная обратная связь (ООС) действует в сторону уменьшения отклонений текущих значений координат объекта от их предшествующих значений, а положительная обратная связь (ПОС) действует в сторону увеличения. Следовательно, ООС позволяет строить наиболее точные САУ, так как несёт в себе информацию обо всех изменениях регулируемой величины; ПОС служит для изменения внутренних свойств отдельных звеньев САУ. Соединение обратной связью
Если задана передаточная Функция W(S), то путём подставки S=jw получаем частотную передаточную функцию W (jw), которая является комплексным выражением т.е.
А(w) – вещественная составляющая К(w) – мнимая составляющая. Частотная передаточная функция может быть представлена в показательной форме
Функция М(w), представленная при изменении частоты от 0 до Ґ получило название амплитудной частотной характеристики (АЧХ).Функция j(w), представленная при изменении частоты от 0 до Ґ называется фазовой частотной характеристикой (ФЧХ). Для анализа поведения системы в большом диапазоне частот удобно в качестве аргумента частотных характеристик рассматривать не частоту ω, а ее десятичный логарифм ω 10 log.
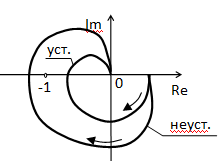
Критерий Найквиста Данный критерий определяет устойчивость по частотным характеристикам системы. Для построения частотных характеристик, например, АФХ требуется подстановка s = jw в передаточную функцию системы, которая, как правило, представляет собой дробно-рациональную функцию. Поэтому данный критерий более сложен для ручного расчета по сравнению с критерием Михайлова. Последовательность: 1) Определяется передаточная функция разомкнутой системы 2) Определяется число правых корней m. 3) Подставляется s = jw: W¥(jw). 4) Строится АФХ разомкнутой системы. Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W¥(jw) m раз полуохватывала точку (-1; 0), где m - число правых корней разомкнутой системы, т.е. корней si > 0.
Eсли АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости (см. рисунок 1.45). В случае, если характеристическое уравнение разомкнутой системы A(s) = 0 правых корней не имеет (т.е. m = 0), то критерий можно переформулировать: замкнутая система устойчива, если АФХ разомкнутой системы W¥(jw) не охватывает точку (-1; 0), в противном случае система неустойчива; если проходит через нее, то на границе устойчивости. Пример. Пусть передаточная функция разомкнутой системы имеет вид
Для построения АФХ разомкнутой системы делается подстановка s = j*w в передаточную функцию:
где
а = (1 – 2*w2)2 + (3,5w3 – 4*w)2 – знаменатель.
По полученным формулам строится АФХ (см. таблицу 1.4 и рисунок 1.46). Характеристическое уравнение правых корней не имеет, АФХ охватывает точку (-1; 0), следовательно, замкнутая система неустойчива. ¨ Точность САР Точность регулирования оценивают по ошибкам, с которыми воспроизводятся заданные значения регулируемых величин. Чем выше точность регулирования, тем меньше должны быть ошибки. В одной и той же системе ошибки получаются различными различными в зависимости от того, каким воздействием задающим, возмущающим или тем и другим одновременно они вызваны. Систему, контур которой не имеет интегрирующих звеньев, называют статической, а при наличии в системе одного или нескольких интегрирующих звеньев – астатической. По числу интегр-их зв-ев определяют порядок астатизма системы, при одном – астатизм первого порядки и т.д. Для определения ошибок в установившемся режиме (при t->∞):
где K, K1 – коэффициент усиления всей разомкн. системы и коэф усил-ия объекта Для систем с астатизмом υ изображение ошибки в установивш. режиме имеет вид: При отсутствии в системе интегрирующих звеньев постоянные воздействия g0 и f0 вызывают постоянную пищьмищьку ε0, которую называют статической. Эта ошибка будет тем меньше, чем больше коэффициент усиления К системы, причем для уменьшения статической ошибки, вызванной возмущающим воздействием, следует увеличить K2 регулятора, а не K1 объекта. В системе с астатизмом первого порядка установившаяся ошибка возникает при воздействиях с постоянной скоростью. Такая ошибка называется скоростной. При воздействиях с постоянным ускорением в системе с астатизмом второго порядка возникает ошибка по ускорению.
Устойчивость линейных САР Важным показателем АСР является устойчивость, поскольку основное ее назначение заключается в поддержании заданного постоянного значения регулируемого параметра или изменении его по определенному закону. При отклонении регулируемого параметра от заданной величины (например, под действием возмущения или изменения задания) регулятор воздействует на систему таким образом, чтобы ликвидировать это отклонение. Если система в результате этого воздействия возвращается в исходное состояние или переходит в другое равновесное состояние, то такая система называется устойчивой. Если же возникают колебания со все возрастающей амплитудой или происходит монотонное увеличение ошибки е, то система называется неустойчивой.
Необходимое и достаточное условие устойчивости формулируется следующим образом: Звено или система называются устойчивыми, если переходная составляющая с течением времени стремится к нулю:
Если выходной сигнал звена или системы y(t) рассматривать как сумму двух составляющих y(t) = yуст + уп(t), где
Рисунок 1.40 Если уп(t) с течением времени стремится к бесконечности, звено или система называются неустойчивыми. Другими словами:
Примеры переходных процессов для каждого случая приведены на рисунке 1.41.
Рисунок 1.41 Для того, чтобы определить, устойчива система или нет, используются критерии устойчивости: 1) корневой критерий; 2) критерий Стодола; 3) критерий Гурвица; 4) критерий Найквиста; 5) критерий Михайлова и др. Первые два критерия являются необходимыми критериями устойчивости отдельных звеньев и разомкнутых систем, однако не являются достаточными для однозначного определения устойчивости. Критерий Гурвица является алгебраическим и может быть использован для определения устойчивости как отдельных звеньев, так и замкнутых систем без запаздывания. При этом он позволяет обойтись без определения корней характеристического полинома, который может иметь достаточно большую степень. Последние два критерия относятся к группе частотных критериев, поскольку определяют устойчивость замкнутых систем по их частотным характеристикам. Их особенностью является возможность применения к замкнутым системам с запаздыванием, которыми является подавляющее большинство систем управления.
39 Критерий устойчивости (Гурвица) Критерий Гурвица, как и критерий Стодола, определяет устойчивость по характеристическому полиному системы без непосредственного вычисления его корней. Однако критерий Стодола является необходимым критерием устойчивости, но не является достаточным. То есть, если по критерию Стодола система неустойчива, то она действительно является неустойчивой, если по критерию система устойчива, то для подтверждения ее устойчивости требуются дополнительные расчеты. Например, характеристический полином s3 + s2 + 2s + 8 по критерию Стодола соответствует устойчивой системе, однако корни этого полинома равны s1 = -2, s2,3 = 0,5 ± j×1,94. То есть система фактически является неустойчивой, хотя коэффициенты полинома положительны. Критерий Гурвица дает необходимое и достаточное условие устойчивости линейных систем. Исходной информацией для данного критерия является характеристический полином системы: разомкнутой A(s) или замкнутой D(s) – в зависимости от того, какая система анализируется. Для определения устойчивости по Гурвицу строится матрица таким образом, чтобы по главной диагонали были расположены коэффициенты ХПЗС с an+1 по a0. Справа и слева от нее записываются коэффициенты с индексами через 2 (a0, a2, a4… или a1, a3, a5 …). Тогда для устойчивой системы необходимо и достаточно, чтобы определитель и все главные диагональные миноры матрицы были больше нуля. Если хотя бы один определитель будет равен нулю, то система будет находиться на границе устойчивости. Если хотя бы один определитель будет отрицателен, то система неустойчива независимо от числа положительных или нулевых определителей. Пример. Дана передаточная функция разомкнутой системы
Требуется определить устойчивость замкнутой системы по критерию Гурвица. Для этого определяется ХПЗС: D(s) = A(s) + B(s) = 2s4 + 3s3 + s2 + 2s3 + 9s2 + 6s + 1 = 2s4 + 5s3 + 10s2 + 6s + 1. Поскольку степень ХПЗС равна n = 4, то матрица будет иметь размер 4х4. Коэффициенты ХПЗС равны а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1. Матрица имеет вид
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители (диагональные миноры матрицы): Δ1 = 5 > 0,
Δ4 = 1* Δ3 = 1*209 > 0. Поскольку все определители положительны, то АСР устойчива.
40 Критерий устойчивости (Найквиста) Данный критерий определяет устойчивость по частотным характеристикам системы. Для построения частотных характеристик, например, АФХ требуется подстановка s = jw в передаточную функцию системы, которая, как правило, представляет собой дробно-рациональную функцию. Поэтому данный критерий более сложен для ручного расчета по сравнению с критерием Михайлова. Последовательность: 1) Определяется передаточная функция разомкнутой системы 2) Определяется число правых корней m. 3) Подставляется s = jw: W¥(jw). 4) Строится АФХ разомкнутой системы. Для устойчивости АСР необходимо и достаточно, чтобы при увеличении w от 0 до ¥ АФХ W¥(jw) m раз полуохватывала точку (-1; 0), где m - число правых корней разомкнутой системы, т.е. корней si > 0.
Если АФХ проходит через точку (-1; 0), то замкнутая система находится на границе устойчивости (см. рисунок 1.45). В случае, если характеристическое уравнение разомкнутой системы A(s) = 0 правых корней не имеет (т.е. m = 0), то критерий можно переформулировать: замкнутая система устойчива, если АФХ разомкнутой системы W¥(jw) не охватывает точку (-1; 0), в противном случае система неустойчива; если проходит через нее, то на границе устойчивости. Пример. Пусть передаточная функция разомкнутой системы имеет вид
Для построения АФХ разомкнутой системы делается подстановка s = j*w в передаточную функцию:
где
а = (1 – 2*w2)2 + (3,5w3 – 4*w)2 – знаменатель.
По полученным формулам строится АФХ (см. таблицу 1.4 и рисунок 1.46). Характеристическое уравнение правых корней не имеет, АФХ охватывает точку (-1; 0), следовательно, замкнутая система неустойчива.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.112.111 (0.22 с.) |








 Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления.
Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления. ; W(s) =
; W(s) = 


 .
. ; W(s) = K*s
; W(s) = K*s
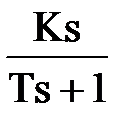 .
. .
. ; W(s) =
; W(s) =  .
. . Тогда изображение выходной величины: Y(s) = W(s) X(s) =
. Тогда изображение выходной величины: Y(s) = W(s) X(s) = 
 .
.
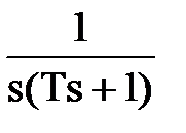 =
= 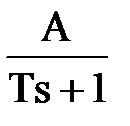 +
+  =
=  =
=  -
-  =
= 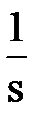 -
- 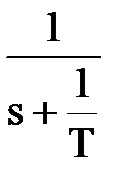
 } = 1, второй: L-1{
} = 1, второй: L-1{  } =
} = 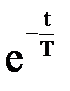 .
. ).
).
 ,
, .
.
 =
=  .
. =
=  - по ошибке,
- по ошибке, =
=  - по возмущению,
- по возмущению,
 , то передаточные функции замкнутой системы могут быть преобразованы:
, то передаточные функции замкнутой системы могут быть преобразованы: =
=  =
=  ,
, =
=  =
= 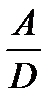 ,
,
 .
. .
. ,
, ,
,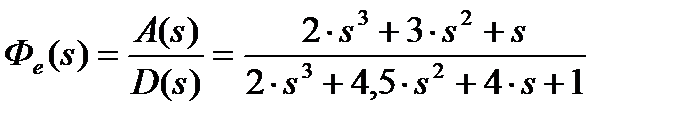 .
. .
.

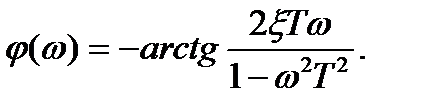

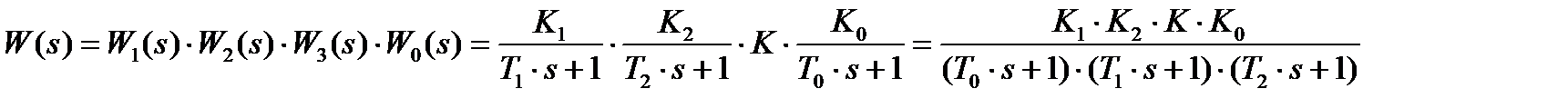 Переведем передаточную функцию разомкнутой системы в комплексные числа, то есть выделим действительную и мнимую части.
Переведем передаточную функцию разомкнутой системы в комплексные числа, то есть выделим действительную и мнимую части.

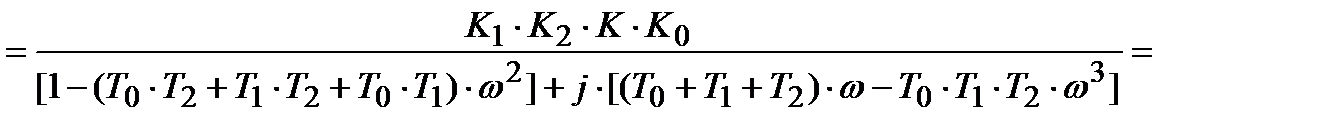


 .
.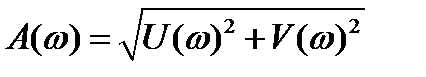

 .
.



 .
.
 .
. ,
, - действительная часть АФХ,
- действительная часть АФХ, - мнимая часть,
- мнимая часть,


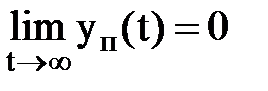 .
. - установившееся значение y(t), уп(t) – переходная составляющая, то уп(t) = y(t) – yуст.
- установившееся значение y(t), уп(t) – переходная составляющая, то уп(t) = y(t) – yуст.
 .
.
 .
.
 ,
,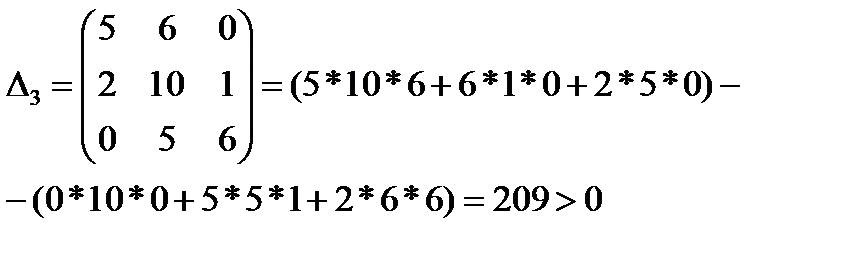
 .
.
 .
.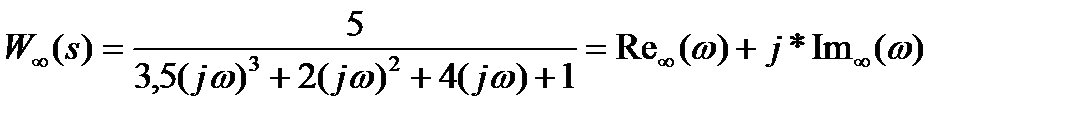 ,
, - действительная часть АФХ,
- действительная часть АФХ,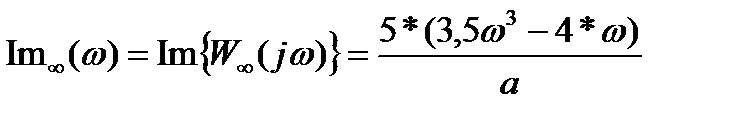 - мнимая часть,
- мнимая часть,


