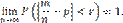Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события: виды событий, действия над событиями. Свойства действий над событиями. Отношения между событиями.Стр 1 из 4Следующая ⇒
Случайные события: виды событий, действия над событиями. Свойства действий над событиями. Отношения между событиями. Случайными событиями мы будем называть любое явление, которое может происходить вокруг нас (или не происходить). События называются несовместными, если появление одного из них исключает появление других. Несовместные, т.е. события, которые не могут произойти одновременно. Теорема: Если события А и В несовместны, то их произведение есть невозможное событие. Полной группой событий называется совокупность всех возможных результатов опыта. Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью. Действия над событиями. 1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произойдет либо событие А, либо событие В, либо, если это возможно, они произойдут одновременно. 2. Произведением А*В событий А и В называется событие, состоящее в том, что события А и В произойдут одновременно. 3. Разностью А\В событий А и В называется событие, состоящее в том, что произойдет та часть события А, которая не входит в В. 4. Событие противоположное к данному. А или дополнение события А.
Частота и относительная частота события. Свойства относительной частоты. Вероятность случайного события. Связь между вероятностью и относительной частотой. Пусть в n опытах некоторое событие А наступило Na раз. Число Na – частота события А.
Свойства: 1) 2) P*() = 0 3) P*(Ω) = 1 4) Если А и В несовместны, то P*(A+В) = P*(A)+ P*(В) Вероятность события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. И определяется формулой: Определение вероятности не требует, чтобы испытания производились в действительности. Определение относительной частоты предполагает, что испытания были произведены фактически. Или вероятность вычисляют до опыта, а относительную частоту – после опыта.
Аксиоматическое определение вероятности. Вероятностью события А называется числовая функция Р(А), удовлетворяющая след. аксиомам вероятности: 1. Р(А) ≥ 0; неотрицательность 2. Р(Ω) = 1, Ω - достоверное событие; 3. Для любых попарно несовместных событий А1, А2…An справедливо следующее равенство: Р(A1+A2+…An)=P(A1)+P(A2)+…+P(An) Следствия из аксиом 1. Вероятность невозможного события равна нулю: P(∅) = 0. 5. Р(A1+A2+…An)=P(A1)+P(A2)+…+P(An) 6. P(A+В) = P(A)+ P(В) Классическое определение вероятности. Вероятность есть число, характеризующее степень возможности появления события. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу, Р (A) = m / n. Свойство 1. Вероятность достоверного события равна единице. Р (A) = m / n = n / n = 1. Свойство 2. Вероятность невозможного события равна нулю. Р (А) = m / n = 0 / n = 0. Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. 0 ≤ Р (А) < 1 Свойство 4. P(A+В) = P(A)+ P(В)
Геометрическая вероятность. Геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.). Вероятность попадания точки на отрезок l определяется равенствомР = Длина l / Длина L. Вероятность попадания точки в фигуру g определяется равенством Р = Площадь g / Площадь G.
Вероятность суммы событий Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. В частности, если два события А и B — несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого. Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р (А + В) = Р (А) + Р (В).
Доказательство: Введем обозначения: n — общее число возможных элементарных исходов испытания; m1 — число исходов, благоприятствующих событию A; m2— число исходов, благоприятствующих событию В.Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m1 + m2. Следовательно,Р (A + В) = (m1 + m2) / n = m1 / n + m2 / n. Приняв во внимание, что m1 / n = Р (А) и m2 / n = Р (В), окончательно получим Р (А + В) = Р (А) + Р (В).
Формула полной вероятности Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий B 1 ,В 2 ,..., Вп, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Формула Байеса Пусть событие A может наступить при условии появления одного из несовместных событий B 1 ,В 2 ,...,Вп, образующих полную группу. Тогда Р(В1/А) = Доказательство: По определению условной вероятности, Р(ВI/A)= Распределение Пауссона. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Если вероятность события мала (р Произведение nр сохраняет постоянное значение, а именно nр = Таким образом, Свойства 1. Функция распределения является неубывающей. 2. Значения функции распределения удовлетворяют неравенствам 3. Если возможные значения случайной величины принадлежат интервалу (a;b), то: 1) F(x)=0 при x ≤a; 2) F(x)=1 при x≥b.
Равномерное распределение. Случайная величина
Нормальное распределение. Нормальное распределение (синоним - гауссово распределение) - распределение непрерывной случайной величины с плотностью
График плотности распределения для нормально распределённой случайной величины имеет вид, отдалённо напоминающий колокол:
Линейная функция регрессии. Рассмотрим двумерную случайную величину (X, Y), где X и У — зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением (точное приближение, вообще говоря, невозможно) величины Y в виде линейной функции величины X:
Теорема. Линейная средняя квадратическая регрессия Y на X имеет вид
Коэффициент β=rσy/σx называют коэффициентом регрессии Y на X, а прямую
Неравенство Маркова. Неравенство Чебышева. Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа ε, не меньше, чем 1 −D[X]ε2 P(|X – M(X)| < ε) ≥ 1 –D(X)ε2 Доказательство. Так как события, состоящие в осуществлении неравенств P(|X−M(X)| < ε) и P(|X – M(X)| ≥ε) противоположны, то сумма их вероятностей равна единице, т. е. P(|X – M(X)| < ε) + P(|X – M(X)| ≥ ε) = 1. Отсюда интересующая нас вероятность P(|X – M(X)| < ε) = 1 − P(|X – M(X)| > ε). Таким образом, задача сводится к вычислению вероятности P(|X –M(X)| ≥ ε). Напишем выражение для дисперсии случайной величины X D(X) = [x1 – M(x)]2p1 + [x2 – M(x)]2p2 +... + [xn – M(x)]2pn Все слагаемые этой суммы неотрицательны. Отбросим те слагаемые, у которых |xi – M(X)| < ε (для оставшихся слагаемых |xj – M(X)| ≥ ε), вследствие чего сумма может только уменьшиться. Условимся считать для определенности, что отброшено k первых слагаемых (не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом,
D(X) ≥ [xk+1 – M(x)]2pk+1 + [xk+2 – M(x)]2pk+2 +... + [xn – M(x)]2pn Обе части неравенства |xj –M(X)| ≥ ε (j = k+1, k+2,..., n) положительны, поэтому, возведя их в квадрат, получим равносильное неравенство |xj – M(X)|2 ≥ε2.Заменяя в оставшейся сумме каждый из множителей |xj – M(X)|2числом ε2(при этом неравенство может лишь усилиться), получим D(X) ≥ ε2(pk+1 + pk+2 +... + pn) По теореме сложения, сумма вероятностей pk+1+pk+2+...+pn есть вероятность того, что X примет одно, безразлично какое, из значений xk+1 +xk+2 +...+xn, а при любом из них отклонение удовлетворяет неравенству |xj – M(X)| ≥ ε. Отсюда следует, что сумма pk+1 + pk+2 +... + pn выражает вероятность P(|X – M(X)| ≥ ε). Это позволяет переписать неравенство для D(X) так D(X) ≥ ε2P(|X – M(X)| ≥ ε) или P(|X – M(X)|≥ ε) ≤D(X)/ε2 Окончательно получим P(|X – M(X)| < ε) ≥D(X)/ε2
Теорема Чебышева. Теорема Чебышева. Если
будет как угодно близка к единице, если число случайных величин достаточно велико. Другими словами, в условиях теоремы
Доказательство. Введем в рассмотрение новую случайную величину — среднее арифметическое случайных величин
Найдем математическое ожидание Х. Пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), получим
Применяя к величине Х неравенство Чебышева, имеем
или, учитывая соотношение (1)
Пользуясь свойствами дисперсии (постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат; дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых), получим
По условию дисперсии всех случайных величин ограничены постоянным числом С, т.е. имеют место неравенства:
поэтому
Итак,
Подставляя правую часть (2) в неравенство (1) (отчего последнее может быть лишь усилено), имеем
Отсюда, переходя к пределу при n→∞, получим
Наконец, учитывая, что вероятность не может превышать единицу, окончательно можем написать
Теорема доказана. Теорема Бернулли. Теорема Бернулли. Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико. Другими словами, если ε — сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство
Доказательство. Обозначим через X1 дискретную случайную величину — число появлений события в первом испытании, через X2 — во втором,..., Xn — в n -м испытании. Ясно, что каждая из величин может принять лишь два значения: 1 (событие A наступило) с вероятностью p и 0 (событие не появилось) с вероятностью
Можно ли применить к рассматриваемым величинам теорему Чебышева? Можно, если случайные величины попарно независимы и дисперсии их ограничены. Оба условия выполняются Действительно, попарная независимость величин Применяя теорему Чебышева (частный случай) к рассматриваемым величинам, имеем
Приняв во внимание, что математическое ожидание a каждой из величин
Остается показать, что дробь
Учитывая это равенство, окончательно получим
Случайные события: виды событий, действия над событиями. Свойства действий над событиями. Отношения между событиями. Случайными событиями мы будем называть любое явление, которое может происходить вокруг нас (или не происходить). События называются несовместными, если появление одного из них исключает появление других. Несовместные, т.е. события, которые не могут произойти одновременно. Теорема: Если события А и В несовместны, то их произведение есть невозможное событие. Полной группой событий называется совокупность всех возможных результатов опыта. Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью. Действия над событиями. 1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произойдет либо событие А, либо событие В, либо, если это возможно, они произойдут одновременно. 2. Произведением А*В событий А и В называется событие, состоящее в том, что события А и В произойдут одновременно. 3. Разностью А\В событий А и В называется событие, состоящее в том, что произойдет та часть события А, которая не входит в В. 4. Событие противоположное к данному. А или дополнение события А.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 3515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.125.2 (0.103 с.) |
 P*(A) - относительная частота (частота).
P*(A) - относительная частота (частота). P*(A)
P*(A) 
 . Где Р(А) — вероятность события A, m — число благоприятствующих событию A исходов, n — общее число возможных исходов.
. Где Р(А) — вероятность события A, m — число благоприятствующих событию A исходов, n — общее число возможных исходов. , где Р (А) = Р (В 1) РВ1 (А) + Р (В 2) РВ2 (А) +...+ Р (Вn) РВn (А)
, где Р (А) = Р (В 1) РВ1 (А) + Р (В 2) РВ2 (А) +...+ Р (Вn) РВn (А) =
= 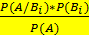
 0, 1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.
0, 1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.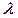 . Это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях n, остается неизменным.
. Это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях n, остается неизменным. Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (р мало) событий.
Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (р мало) событий. <
<  . Так как вероятность любого события неотрицательна, то
. Так как вероятность любого события неотрицательна, то  . Поэтому из формулы следует, что
. Поэтому из формулы следует, что 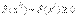 , т.е.
, т.е.  .
. . Это свойство вытекает из того, что F(x) определяется как вероятность. Ясно, что
. Это свойство вытекает из того, что F(x) определяется как вероятность. Ясно, что  и
и 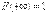 .
. имеет равномерное распределение на отрезке [a,b], если она непрерывна, принимает значения только на отрезке [a,b], а плотность ее распределения постоянна на отрезке [a,b], и равна 0 вне этого отрезка.
имеет равномерное распределение на отрезке [a,b], если она непрерывна, принимает значения только на отрезке [a,b], а плотность ее распределения постоянна на отрезке [a,b], и равна 0 вне этого отрезка.
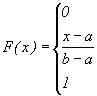

 Здесь "мю" - математическое ожидание, "сигма" - среднеквадратическое отклонение (корень квадратный из дисперсии). Функция распределения не может быть записана через элементарные функции, поскольку интеграл от плотности распределения "неберущийся". Поэтому её записывают вот так:
Здесь "мю" - математическое ожидание, "сигма" - среднеквадратическое отклонение (корень квадратный из дисперсии). Функция распределения не может быть записана через элементарные функции, поскольку интеграл от плотности распределения "неберущийся". Поэтому её записывают вот так: Вероятность того, что непрерывная случайная величина окажется каким-либо действительным числом, равна единице, поскольку полагается, что величина может принимать значение только на множестве действительных чисел. Поэтому
Вероятность того, что непрерывная случайная величина окажется каким-либо действительным числом, равна единице, поскольку полагается, что величина может принимать значение только на множестве действительных чисел. Поэтому

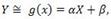 где α и β — параметры, подлежащие определению.
где α и β — параметры, подлежащие определению.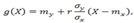 где mx=M(X), my=M(Y), σx=√D(X), σy=√D(Y), r=µxy/(σxσy)— коэффициент корреляции величин X и Y.
где mx=M(X), my=M(Y), σx=√D(X), σy=√D(Y), r=µxy/(σxσy)— коэффициент корреляции величин X и Y.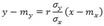 называют прямой среднеквадратической регрессии Y на X.
называют прямой среднеквадратической регрессии Y на X.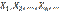 — попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С ), то, как бы мало ни было положительное число ε, вероятность неравенства
— попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С ), то, как бы мало ни было положительное число ε, вероятность неравенства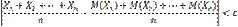
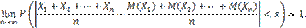
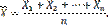
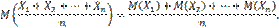 (1)
(1)
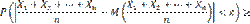
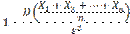
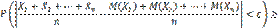
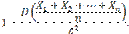
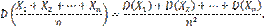
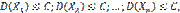
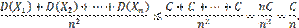
 (2)
(2)
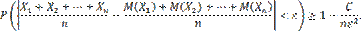
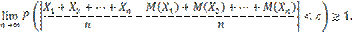
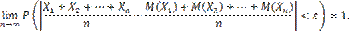
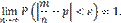
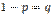 .
.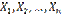 следует из того, что испытания независимы. Дисперсия любой величины
следует из того, что испытания независимы. Дисперсия любой величины  равна произведению
равна произведению 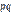 ; так как
; так как 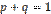 , то произведение
, то произведение 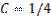 .
.
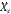 (т.е. математическое ожидание числа появлений события в одном испытании) равно вероятности p наступления события, получим
(т.е. математическое ожидание числа появлений события в одном испытании) равно вероятности p наступления события, получим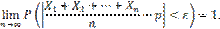
 равна относительной частоте
равна относительной частоте 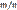 появлений события A в испытаниях. Действительно, каждая из величин
появлений события A в испытаниях. Действительно, каждая из величин 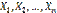 при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма
при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма 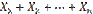 равна числу
равна числу  появлений события в
появлений события в 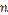 испытаниях, а значит,
испытаниях, а значит,