
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад 11.1. Побудова полігональної моделі сфери сіткою із паралелей та меридіанів.
Найзручнішою для моделювання сфери є сферична система координат (рис.11.2), в якій точка М на сфері з радіусом R визначається значенням полярного кута j в діапазоні від 0 до 2p та сферичного кута q в діапазоні від 0 до p. Координати вершин апроксимуючої сітки обчислюються з допомогою двох циклів, в першому з яких зі сталим кроком змінюється від від 0 до 2p кут j,в другому – від 0 до p кут q. Для переходу від сферичної до декартової системи координат використовуються співвідношення x = R cos j sin q, y = R sin j sin q, z = R cos q. (11.1)
Рис.11.2. Полігональна модель сфери та сферична система координат.
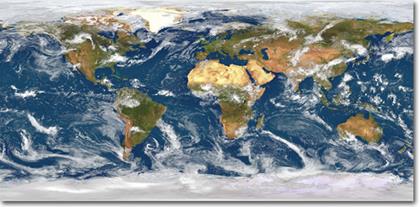
Рис.11.3. Відповідність координат текстури і кутів сфери. Для обчислення текстурних координат використовуються лінійні співвідношення (рис11.3) s = j / ( 2 p), t = 1 - q / p (11.2) Процедура побудова полігональної моделі сфери сіткою із паралелей та меридіанів. R – радіус сфери, n1, n2 – кількість перерізів в двох напрямах (густина сітки); k1, k2 – кількість повторів текстури в двох напрямах. procedure DrawSphere(R:GLfloat; n1,n2:GLint;k1,k2:GLfloat); var i,j,k:GLint; teta, fi, z,delta_fi,delta_teta, delta_s,delta_t,cos_fi,sin_fi,c,s,t,R1:GLfloat; begin delta_fi:=2*pi/n2; delta_teta:=Pi/n1; delta_s:=k2/n2; delta_t:=k1/n1; teta:=-pi; glCullFace (GL_BACK); glEnable (GL_CULL_FACE); for j:=0 to n1-1 do begin fi:=0; glBegin (GL_QUAD_STRIP); for i:=0 to n2 do begin for k:=1 downto 0 do begin t:=teta+k*delta_teta; s:=sin(t); c:=cos(t); R1:=R*s; cos_fi:=cos(fi); sin_fi:=sin(fi); glTexCoord2d (i*delta_s, (j+k)*delta_t); glNormal3f (cos_fi*s, sin_fi*s, c); glVertex3f (R1*cos_fi,R1*sin_fi,R*c); end; fi:=fi+delta_fi end; glEnd; teta:=teta+delta_teta end end; Примітка. Для зменшення кількості операцій та спрощення обчислення текстурної координати t у вищенаведеній процедурі кут q змінюється від p до 2p. Приклад 11.2. Геосфера. В програмах комп’ютерної графіки часто використовується зображення земної кулі у вигляді сфери з з нанесеною текстурою (рис.11.4). Для одержання зображення на рис.11.5 достатньо підібрати відповідну текстуру і використати вищенаведену процедуру (задати розміри і назву файла, змінити точку зору і задати напрям обертання навколо вертикальної осі). Тонкий шар атмосфери навколо земної кулі можна імітувати з допомогою ефекту туману на границі між сферою і темним фоном.
Рис.11.4. Зображення земної поверхні (циліндрична рівноінтервальна проекція).
Рис.11.5. Сфера з нанесеним Рис.11.6. Геосфера з нанесеною зображенням земної поверхні сіткою меридіанів і паралелей. (геосфера).
Для нанесення сітки з меридіанів і паралелей (рис.11.6) потрібно після виведення текстурованої сфери відключити текстуру, задати колір і товщину ліній, режим виведення многокутників у вигляді ліній та повторно вивести сферу більшого радіуса. Для імітації хмарного покрову над земною поверхнею можна використати текстуру з хмарами (рис.11.7) або спеціальну напівпрозору текстуру (рис.11.8) вивести на сферу більшого радіуса, використавши приклад 4.6. Для сфери з хмарним покриттям додати додаткове обертання.
Рис.11.7. Зображення земної поверхні з хмарами.
Рис.11.8. Напівпрозора текстура хмарного покриття. На космічних знімках помітні бліки від сонячних променів на поверхнях океанів і гірських масивів. З використанням відповідної текстури, на якій всі неблікуючі ділянки зафарбовані чорним кольором, до зображення геосфери можна додати бліки, використавши приклади 4.2, 4.6, 10.2. Приклад 11.3. Побудова сфери тріангуляцією ікосаедра (рис.11.9,11.10). При використання сітки із трикутників однакового розміру більш якісно моделюється освітленість порівняно з нерівномірною сіткою із прикладу 11.1, але потрібен складніший алгоритм для обчислення текстурних координат і усунення крайових ефектів.
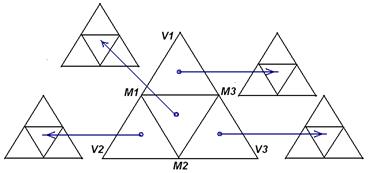
Рис. 11.9. Апроксимація сфери правильними трикутниками
Рис. 11.10. Розбиття трикутника на кожному кроці рекурсивного алгоритму тріангуляції сфери.
Текстурні координати задаються для трикутників останнього рівня вкладеності. Для обчислення текстурних координат вершин потрібно від декартових координат x,y,z перейти до полярного кута j та сферичного q (рис.11.2, 11.3). Із формул (11.1) tg j = y/x, ctg j = x/y, cos q = (z/R), (11.3) причому кут j змінюєтьсяв діапазоні від 0 до 2p, а кут q в діапазоні від 0 до p. Полярний кут j залежить тільки від співвідношення x та y. При j = arctg(y / x), (11.4) при j = arcсtg(x / y)= p/2 - arctg(x / y). (11.4а)
|
|||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.156.156 (0.01 с.) |








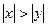 більшу точність дає обчислення кута j за формулою
більшу точність дає обчислення кута j за формулою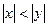 більшу точність дає обчислення кута j за формулою
більшу точність дає обчислення кута j за формулою


