
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обробка результатів експерименту і їх аналіз
1. За формулою (4) обчислити значення коефіцієнта в’язкості досліджуваної рідини за даними вимірювань для кожної кульки окремо. 2. Знайти середню абсолютну і відносну похибки визначення коефіцієнта в’язкості і записати кінцевий результат:
Контрольні запитання 1. Явища переносу. Молекулярно-кінетичний механізм явищ переносу. 2. Закони Фіка, Фур’є і Ньютона. 3. Коефіцієнти явищ переносу і їх фізичний зміст. 4. Зв’язки між коефіцієнтами дифузії, в’язкості і теплопровідності. 5. Експериментальні методи визначення коефіцієнта в’язкості. 7. Вияснити основні джерела похибки у даній роботі.
Лабораторна робота № 7.4 Мета роботи: визначити коефіцієнт теплопровідності міді. Прилади та матеріали: прилад для визначення коефіцієнта теплопровідності; термометри (4 шт.); секундомір, балон для зливання води; мензурка; штангенциркуль. Теоретичні відомості Метод визначення коефіцієнта теплопровідності металів, що застосовується в цій роботі, ґрунтується на вимірюванні кількості теплоти Q Дж/с, що проходить за одиницю часу через поперечний переріз S металевого (мідного) стержня. Як відомо, цей тепловий потік за законом Фур'є визначається за формулою Q=кSgradT, (1) де к — коефіцієнт теплопровідності;
З формули (1) випливає, що коефіцієнт теплопровідності дорівнює:
Він чисельно дорівнює кількості теплоти, що переноситься через одиницю площі (1 м2) поперечного перерізу зразка за одиницю часу (1 с) при спаді температури на 1°С на одиниці шляху (1 м) теплового потоку, тобто к = Вт/м×К Постійність градієнта температури вздовж зразка забезпечується нагріванням одного з його кінців в електричній печі і охолодженням іншого його кінця проточною водою, що має постійну температуру t1 °C. З іншого боку, кількість теплоти, що проходить через зразок і передається воді за одиницю часу, може бути знайдена з рівняння теплового балансу:
де с — питома теплоємність води, Дж/кг×К; m — маса води, що протікає через холодильник за 1 с, кг; t° — температура, до якої нагрівається вода, що оточує холодний кінець зразка. Прирівнюючи праві частини рівнянь (1) і (2), одержуємо такий вираз для коефіцієнта теплопровідності:
Враховуючи особливості конструкції установки, що застосовується в роботі (рис.7.4.1) формулу (3) можна перетворити відносно до виду вимірюваних величин. Установка для визначення теплопровідності складається з мідного стержня 3, що має площу поперечного перерізу S=70,0×10-6 м2, електричного нагрівника 5, водяного холодильника 2, гнізд для термометрів 4, посудини 1 з охолодженою водою і мензурки 6. Градієнт температури можна записати через різницю показів термометрів t3 і t4 і відстань l між ними:
Рис. 7.4.1. Масу води, що протікає через холодильник за одиницю часу, виразимо через її об'єм і густину:
де r — густина води; V — об'єм води, що витікає за час t. Підставляючи формули (4) і (5) в (3), одержуємо кінцевий вираз для розрахунку коефіцієнта теплопровідності міді, з якої виготовлено зразок, то досліджується:
Хід роботи 1. Штангенциркулем виміряти відстань l між термометрами t3 і t4, а також записати значення площі поперечного перерізу мідного стержня S (наводиться в інструкції до установки) і увімкнути нагрівач. 2. Після достатнього прогрівання стержня відкрити кран і повільно пропускати воду через холодильник. Потік охолоджувальної води регулюють таким чином, щоб досягти максимальної різниці температур, що реєструються термометрами t3 і t4. 3. Після встановлення стаціонарного режиму теплопередачі, якому відповідає сталість показань всіх термометрів, вимірюють температури t1, t2, t3 і t4. 4. При такому установленому потокові охолоджувальної води секундоміром заміряють час t, протягом якого в мензурці 6 збирається деякий її об'єм (наприклад, 100 см3). 5. З таблиць знаходять теплоємність води с і її густину r при температурних умовах досліду. 6. Результати вимірювань записують в таблицю.
|
|||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.85.33 (0.005 с.) |
 .
.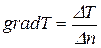 — градієнт температури, К/м.
— градієнт температури, К/м. .
.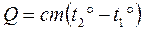 , (2)
, (2) , (3)
, (3)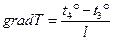 . (4)
. (4)
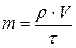 , (5)
, (5) . (6)
. (6)


