
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
С.Г.Авдєєв, Т.І.Бабюк, П.В.Гель, О.С. КамінськийСтр 1 из 7Следующая ⇒
С.Г.Авдєєв, Т.І.Бабюк, П.В.Гель, О.С. Камінський ЛАБОРАТОРНИЙ ПРАКТИКУМ З ФІЗИКИ Частина 3 (ядерна фізика, статистична фізика і термодинаміка, фізика твердого тіла) Міністерство освіти і науки України Вінницький національний технічний університет С.Г.Авдєєв, Т.І.Бабюк, П.В.Гель, О.С. Камінський ЛАБОРАТОРНИЙ ПРАКТИКУМ З ФІЗИКИ Частина 3 (ядерна фізика, статистична фізика і термодинаміка, фізика твердого тіла)
Затверджено Вченою радою Вінницького національного технічного університету як лабораторний практикум для студентів університету. Протокол №8 від 2 березня 2006 року.
Вінниця ВНТУ 2006 УДК 53 (075) А 75
Рецензенти: П.М. Зузяк, доктор фізико-математичних наук, професор В.Г. Дзісь, кандидат технічних наук, доцент І.О. Сівак, доктор технічних наук, професор
Рекомендовано до видання Вченою радою Вінницького національного технічного університету Міністерства освіти і науки України
Авдєєв С.Г., Бабюк Т.І., П.В.Гель, О.С. Камінський А75 Лабораторний практикум з фізики, ч.3 (ядерна фізика, статистична фізика і термодинаміка, фізика твердого тіла). Лабораторний практикум. Видання третє, перероблене і доповнене. – Вінниця: ВНТУ, 2006. - 122с.
Посібник складено відповідно до діючої програми з курсу фізики для технічних вузів і пропонується студентам всіх форм навчання.
УДК 53 (075)
© С.Г. Авдєєв, Т.І. Бабюк, П.В. Гель, О.С. Камінський, 2006 ЗМІСТ
Розділ перший. ФІЗИКА АТОМА ТА ЯДРА Лабораторна робота № 6.1
Мета роботи: за допомогою торцевого лічильника з досить тонким вхідним вікном виміряти залежність N(х)=f(х) і розрахувати енергію a частинок. Прилади і матеріали: перерахувальний прилад ПСО-2,4 в комплекті з блоком детектування a-випромінювання; радіоактивний препарат Рu239.
Теоретичні відомості Явище a- розпаду було відкрите в результаті вивчення природної радіоактивності хімічних елементів. Такі елементи розміщені в кінці періодичної системи Д.І. Менделєєва. Всього нараховується біля 40 природних і більше 100 штучних a-випромінювачів. Рівняння a-розпаду має вигляд:
де
Внаслідок випромінювання a-частинок заряд ядра зменшується на дві одиниці, а масове число – на чотири одиниці. Енергія Еa>0 тому a-розпад можливий в тому випадку, коли маса материнського ядра більша маси дочірнього ядра і атома гелію. Процес a розпаду має дві особливості, які були виявлені на основі експериментального вивчення a-розпаду. Зупинимось на цих особливостях. 1. Стала розпаду l і енергія a-частинок пов’язані законом Гейгера-Неттола, тобто: lnl=B1lnEa+B2. (2)
Для всіх сімейств радіоактивного розпаду стала B1 одна і та ж, а В2 змінюється від одного до іншого сімейства. Із закону Гейгера-Неттола випливає, що чим коротший час життя a-випромінювача, тим більша енергія a-частинок. 2. Енергія a-частинок для різних a-випромінювачів змінюється від 4 до 9 МеВ. Ця енергія значно менша тієї енергії, яку a-частинки повинні були одержати після розпаду за рахунок прискорення в електричному полі ядра. Тобто a-частинки після виходу з ядра повинні прискорюватись до енергії не менше ніж 30 МеВ. Однак експериментально спостерігаються лише a-частинки з енергіями від 4 до 9 МеВ. Як пояснити закон Гейгера-Неттола? Чому енергія випромінюваних a частинок порівняно невелика? Відповіді на ці запитання дає квантова фізика. Перед початком a-розпаду у багатьох ядрах уже є a-частинки. Ці частинки, рухаючись у ядрі, мають енергію
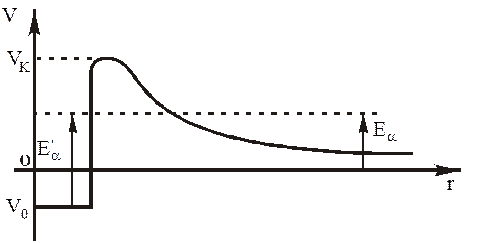
На рис. 6.1 1: V0 – глибина потенціальної ями; Vк – висота потенціального бар’єра;
Еa – енергія a-частинки після виходу з ядра. Вилітаючи з ядра, a-частинки мов би не помічають потенціального бар'єра. Згідно із законами квантової фізики a-частинкам притаманні хвильові властивості. Тому при попаданні на стінку потенціального бар’єра вони відбиваються від неї, як хвилі. Однак від стінки відбиваються не всі a -частинки. Деяка частина з них проникає крізь стінку і вилітає за межі радіоактивних ядер, маючи при цьому енергію Еa. Процес проникнення a-частинок крізь потенціальний бар’єр називається тунельним ефектом. Отже, потенціальний бар'єр для квантових частинок має деяку прозорість.
З ростом енергії
Рис. 6.1.1 Енергія a-частинок залежить від енергетичного стану дочірнього ядра після a-розпаду. Якщо дочірнє ядро знаходиться в основному (не збудженому) стані, то випромінюються лише моно-енергетичні a-частинки. Якщо ж новоутворене ядро може бути як в основному, так і в збудженому станах, то випромінюються декілька енергетичних груп a- частинок і g-квантів. На рис. 6.1.2 подана схема розпаду Для a-розпаду Перехід новоутвореного ядра із збудженого стану в основний стан супроводжується випромінюванням двох g- квантів з енергіями 0,189 МеВ і 0,389 МеВ. Для визначення енергії a-частинок за довжиною вільного пробігу в повітрі слід розглянути механізм взаємодії a- випромінювання з речовиною. Заряджена частинка, рухаючись в речовині, встигає пролетіти деяку відстань перед тим, як втратить всю свою кінетичну енергію. Шлях зарядженої частинки в речовині до повної її зупинки називають лінійним пробігом. Лінійний пробіг визначається питомими втратами енергії. Чим більші густина атомних електронів і заряд частинки, тим більші втрати і тим менший пробіг цієї частинки в речовині. Важкі заряджені частинки, взаємодіючи в основному з атомними електронами, майже не відхиляються від початкового напрямку руху. Це говорить про те, що імовірність взаємодії з ядрами атомів досить низька.
Рис. 6.1.2 Одноразова максимальна втрата енергії a-частинкою при центральному зіткненні з електроном атома може бути оцінена за формулою:
де m – маса електрона; М – маса a-частинки; Еa – кінетична енергія a частинки до зіткнення. Наприклад, для енергії Еa=5,5 МеВ (DЕ)max=3 кеВ. Якщо a- частинка при взаємодії з електронами атомів кожний раз втрачає половину максимальної енергії (DЕ)max, то до повної зупинки вона зіткнеться не менше 3700 разів.
Для визначення довжини вільного пробігу a-частинок в повітрі слід побудувати залежність N(x) числа частинок, які реєструються блоком детектування на різних відстанях від a-випромінювача, від відстані Х. Графік цієї залежності показаний на рис. 6.1.3
Рис. 6.1.3 Як видно з рис. 6.1.3, число зареєстрованих на різних відстанях х a– частинок спочатку трохи зростає, а потім різко спадає. Це пояснюється тим, що іонізаційні властивості a- частинок при зменшенні їх швидкості різко зростають. Точка перегину А характеризує середній пробіг R0 a- частинок у повітрі. Дотична, яка проходить через точку А, екстраполює найбільш прямолінійну частину цієї кривої з віссю х, дає значення екстрапольованого пробігу Re. Різниця Re-R0=d приймається, як правило, за міру розкиду пробігів a-частинок. Для a- частинок з енергією Е=5 МеВ, d/R0=0,01. З ростом енергії a-частинок значення відношення d/R0 зменшується. Оскільки величина d/R0 досить мала, то пробіг частинок у повітрі однозначно визначається їх енергією. У повітрі при нормальних умовах зв’язок міх середнім пробігом R0 (см) і втратами енергії a-частинок Е (МеВ) виражається формулою: R0=0.318E1.5. (4) Ця формула добре збігається з експериментальними даними для a-частинок, енергія яких перебуває в межах 4 £Е£ 9 МеВ. Порядок виконання роботи У лабораторній роботі використовується блок детектування, реєструвальний пристрій якого виконаний на основі люмінофора ZnS, активованого атомами срібла. Ефективність спрацьовування такого пристрою не нижча 20%. Світлові імпульси вловлюються фотопомножувачем і багаторазово підсилюють створену ними електронну емісію. Перерахунковий прилад ПСО-2,4 дає можливість зареєструвати практично кожний імпульс на цифровому табло. Увага! у лабораторній роботі використовується небезпечний радіоактивний препарат Рu239. Період піврозпаду 2,44×104 років. Тому при виконні роботи будьте уважними! 1. Ознайомитись з лабораторною установкою за інструкцією або з допомогою лаборанта. Мікрометричний гвинт, на торці якого укріплено радіоактивний препарат Рu239, встановити на нуль. При цьому препарат буде знаходитись на мінімальній відстані від флуоресціюючого екрана. 2. Провести вимірювання числа N(x) a-частинок через кожен 1 мм відстані препарата від поверхні лічильника (два повних оберти мікрогвинта). Час вимірювання t=100 с. Результати вимірювань занести до таблиці.
3. Побудувати графік залежності кількості зареєстрованих a-частинок від відстані X між препаратом і лічильником. 4. Визначити величину середнього пробігу R0 a-частинок згідно з описом в теоретичних відомостях і рис. 6.1.3. 5. Користуючись формулою (4) теоретичних відомостей, знайти втрати енергії a-частинками на іонізацію молекул повітря.
6. Оцінити точність виконаних розрахунків. Контрольні запитання 1. Записати правило зміщення для a-розпаду і дати його характеристику. 2. Як пояснити закон Гейгера-Неттола? 3. Чому енергія випромінюваних a-частинок порівняно невелика? 4. Чому енергетичний спектр a-випромінювання має дискретний характер? 5. Як взаємодіють a-частинки з молекулами речовини? 6. Як знаходять довжину вільного пробігу a-частинок у повітрі та втрати енергії на іонізацію молекул повітря? 7. При радіоактивному розпаді Рu239 a-частинки що вилітають мають енергію Еa=5,5 МеВ. На іонізацію молекул повітря витрачена енергія, яка знайдена в цій роботі. Де поділась решта енергії (Еa-Е)?
Лабораторна робота № 6.2
Мета роботи: освоїти один із методів визначення активності джерела Прилади і матеріали: перерахунковий прилад ПСО-2,4 з блоком детектування; джерело і -випромінювання Sr90.
Теоретичні відомості Процес самовільного перетворення нестійких ізотопів одних хімічних елементів в ізотопи інших елементів з випромінюванням елементарних частинок або ядер легких хімічних елементів називається радіоактивністю. Явище радіоактивності обумовлене лише внутрішньою будовою ядра і не залежить від зовнішніх умов (тиску, температури, агрегатного стану та ін.). Всі спроби вплинути на хід радіоактивного розпаду не дали бажаних результатів. Радіоактивний розпад не завжди закінчується утворенням стабільного ядра. У багатьох випадках спостерігаються ланцюжки радіоактивних розпадів, в яких ядра знаходяться в близькій взаємодії одне з одним. Такі радіоактивні ланцюжки називають радіоактивними рядами. Серед природних радіоактивних речовин є принаймні три елементи, період піврозпаду яких є одного порядку з віком Землі, приблизно рівним 4,5×109 років. До них відносяться ізотопи 92U238 (Т1/2=4,5×109 років), 92U235 (Т1/2=7,13×108 років), і 90Th232 (Т1/2=1,4×1010 років). Ці елементи розміщені в кінці періодичної системи Менделєєва і входять до групи актиноїдів. Вони дають початок трьом природним радіоактивним рядам: урану (92U238), актинію (92U235) і торію (90Th232). Імовірність радіоактивного розпаду l ядра за одиницю часу є сталою величиною для даного елемента. Звідси випливає, що число актів радіоактивного розпаду dN за інтервал часу dt пропорційне кількості радіоактивних ядер N(t) в момент часу t.
Величину l, яка має розмірність с-1 називають сталою радіоактивного розпаду. Знак мінус у співвідношенні (1) вказує на зменшення числа радіоактивних ядер з часом. Інтегрування диференціального рівняння (1) після поділу змінних дає вираз:
де В – константа інтегрування. При t=0 число радіоактивних ядер було, рівним N0. Тому:
З (2) і (3) одержимо:
Або
Потенціюючи вираз (5), одержимо:
Рівняння (6) відоме під назвою закону радіоактивного розпаду. В цьому рівнянні: N(t) – число ядер, які не розпались на момент часу t; N0 – початкове число атомних ядер; l – стала радіоактивного розпаду. Кількість ядер, які розпадаються за час t, визначається співвідношенням:
Час, за який розпадається половина початкового числа ядер, називається періодом піврозпаду Т. Величина Т визначається із співвідношення:
звідки:
де Нові продукти розпаду можуть бути також радіоактивними. Якщо період піврозпаду препарату «А» значно більший періоду піврозпаду препарату «В», то число ядер NB виражається через число ядер NА таким співвідношенням:
Через деякий час t між радіоактивними нуклідами «А» і «В» наступить рівновага, тобто;
Будь-який радіоактивний розпад характеризується активністю розпаду, тобто числом розпадів за одиницю часу. Із закону радіоактивного розпаду легко визначити активність А:
де Тому:
Одиницею активності будь-якого препарату є 1 Бк (Бекерель), тобто один акт розладу за 1с. ( Дещо раніше користувались одиницею активності в 1 Кі (кюрі). І Кі = 3,7×1010 Бк. Слід відмітити, що хімічно чистий радій масою 1 г якраз має активність в 1 Кі. Після відкриття явища радіоактивного розпаду було виявлено, що різні ядра розпадаються по-різному, з випромінюванням різних частинок. Розрізняють три основні види радіоактивності, які позначають грецькими буквами a, b і g. Розглянемо детальніше природу b-розпаду. Бета-розпадом називається група перетворень атомних ядер, при яких один із нейтронів в ядрі перетворюється в протон або один із протонів у ядрі перетворюється в нейтрон. Одна із особливостей b- розпаду – це суцільний енергетичний спектр b-частинок. Розподіл b-частинок подано на рис. 6.2.1: Енергія b- частинок змінюється від нуля до максимального значення. Енергетичний спектр b-частинок вимірюється магнетним b-спектрометром. Крім електронів (позитронів) при b- розпаді випромінюється нейтрино n0 (антинейтрино Енергія b- частинки
Рис. 6.2.1 Згідно з сучасною теорією ядро, яке містить надлишок нейтронів порівняно зі стабільним ядром з таким же порядковим номером Z, здатне на b-розпад. При цьому в ядрі відбувається перетворення одного із нейтронів в протон:
де +1р1 – протон; -1b0 – електрон;
Якщо ж ядро має надлишок протонів, порівняно з числом нейтронів, то в ядрі можливе перетворення:
де 0n1 – нейтрон; -1b0 – позитрон; n0 – нейтрино. Таке перетворення протона в нейтрон (13) можливе лише в ядрі. Вільний протон не може мати достатньої енергії для такого перетворення. Джерелом додаткової енергії можуть бути нуклони в збудженому ядрі. Існує ще один вид b-розпаду, який пов’язаний із захопленням ядром одного із електронів оболонки атома. В результаті один із протонів ядра перетворюється в нейтрон, випускаючи при цьому нейтрино:
Дочірнє ядро може виявитись у збудженому стані, тому воно здатне на випромінювання одного або кількох g-фотонів. Захоплення електрона ядром може відбутись з К-, L- або М-оболонки атома. Заповнення утворених вакансій більш високо розміщеними електронами приводить до рентгенівського випромінювання, за допомогою якого і було виявлене електронне захоплення у 1937 році.
Порядок виконання роботи Перед виконанням лабораторної роботи слід ознайомитись за інструкцією або за допомогою лаборанта з будовою і порядком роботи на перерахунковому приладі ПСО-2,4. 1. Привести лабораторну установку в робочий стан, при цьому цифрове табло повинно висвічувати нулі. 2. Виміряти радіоактивний фон Nф. Час вимірювання фону t=100 с. Дослід проробити тричі. 3. Одержати у лаборанта досліджуваний і еталонний радіоактивні зразки. Протягом часу t = 100 с виміряти число імпульсів від кожного препарату. Кожний дослід виконати не менше трьох разів. Результати вимірювань фону і препаратів занести до таблиці:
4. Визначити активність досліджуваного радіоактивного препарату, користуючись формулою:
де Ает – активність еталонного препарату, яка згідно з паспортом рівна 2×103 Бк;
5. Оцінити похибки вимірювань. Контрольні запитання І. Який фізичний зміст сталої радіоактивного розпаду та який зв’язок має ця стала з періодом піврозпаду? 2. Вивести закон радіоактивного розпаду. 3. Які процеси відбуваються у ядрах при різних видах b- розпаду? 4. Записати і дати пояснення правил зміщення для трьох видів b- розпаду? 5. На якому принципі працює лічильник Гейгера-Мюллера? 6. В яких одиницях вимірюється активність радіоактивних препаратів? Лабораторна робота № 6.3 ВИЗНАЧЕННЯ ЛІНІЙНОГО КОЕФІЦІЄНТА ОСЛАБЛЕННЯ І ЕНЕРГІЇ ГАММА-КВАНТІВ У СВИНЦІ ДЛЯ Co60 Мета роботи: ознайомитись з експериментальним методом визначення лінійного коефіцієнта ослаблення гамма-квантів у речовині та визначити їх енергію. Прилади і матеріали: експериментальна установка, до складу якої входять: перерахунковий пристрій, лічильник Гейгера; радіоактивний препарат Co60 та свинцеві пластинки.
Теоретичні відомості Проходячи через речовину, g- кванти рухаються зі швидкістю світла і або зовсім не взаємодіють з частинками речовини, або при взаємодії можуть віддавати повністю чи частково свою енергію. Механізм взаємодії g-випромінювання буде розглянуто нижче. Із проходженням пучка g- випромінювання через речовину число g- квантів в ньому поступово зменшується. Зменшується також інтенсивність цього випромінювання. Детальний аналіз показує, що інтенсивність g- квантів у вузькому пучку при проходженні через речовину зменшується за експоненціальним законом: І=І0е-mх, (1) де Іо – початкова інтенсивність; І – інтенсивність пучка g- квантів після проходження шару речовини товщиною х; m – коефіцієнт ослаблення, який залежить від властивостей речовини і енергії g-квантів. Товщина шару поглинальної речовини, при якій інтенсивність падаючого пучка зменшується вдвоє, називається товщиною половинного ослаблення. Знайдемо цю величину:
Звідки
Для 10 – кратного ослаблення ця товщина дорівнює:
Відомо біля десяти процесів взаємодії з речовиною, з яких основним є: фотоефект, комптонівське розсіювання і народження електронно-позитронних пар. Тому коефіцієнт ослаблення g- квантів можна подати у вигляді суми трьох складових m=mф+mк+mп, (4) де mф, mк, mп – лінійні коефіцієнти ослаблення відповідно за рахунок фотоефекту, комптонівського розсіювання і утворення електронно-позитронних пар. Для знаходження залежності коефіцієнта ослаблення від енергії g-квантів і властивостей речовини зупинимось на процесах поглинання дещо детальніше. Фотоефект Електрон, який знаходиться в атомі, не можна вважати вільним. Між ним і ядром (а також і іншими електронами) діють сили взаємодії. Тому при поглинанні g-кванта електроном, який знаходиться в атомі, деяка частина енергії імпульсу передається ядру атома. Як показують розрахунки, в цьому випадку закони збереження енергії і імпульсу завжди можуть бути виконані одночасно. При цьому електрон набуває значної енергії і, як правило, залишає атом. Енергія фотоелектронів дорівнює різниці між енергією Ее = Еg – Ее.з, (5) де Еg – енергія g- кванта; Ее.з – енергія зв'язку електрона в атомі. Якщо електрон вилітає з внутрішньої електронної оболонки, то на неї переходить електрон з більш високої оболонки і заповнює вакансію. Різні енергії зв'язку електронів на цих двох оболонках є причиною появи рентгенівського випромінювання і електронів Оже, які мають незначну енергію. Поява рентгенівського випромінювання і електронів Оже, продовжується до тих пір, поки атом не повернеться в свій основний енергетичний стан. Фотоефект, електрони Оже і рентгенівське випромінювання викликають інтенсивну вторинну іонізацію при взаємодії з атомами поглинальної речовини. Імовірність процесу фотоефекту зменшується із збільшенням енергії g- квантів і росте в залежності від росту порядкового номера поглинальної речовини в таблиці Менделєєва:
де Z – порядковий номер поглинальної речовини; r – густина поглинальної речовини; Еg – енергія g-квантів. Фотоефект найбільш інтенсивний у випадку внутрішніх, міцно зв'язаних електронів і є домінуючим для енергій Комптонівське розсіювання. g- кванти більш високих енергій взаємодіють швидше не з полем всього атома (як у випадку фотоефекту), а з окремим електроном. У цьому випадку поглинання електроном Енергія розсіяного g-фотона Е΄ при комптонівському розсіюванні дорівнює: Е΄g = Еg - Еек, (7) де Еg – енергія падаючого g-фотона; Еек – кінетична енергія розсіяного електрона. Довжина хвилі розсіяного g-фотона пов'язана з довжиною хвилі падаючого g-фотона формулою Комптона:
де m0 – маса електрона; с – швидкість світла; h – стала Планка; q – кут розсіювання; l' – довжина хвилі розсіяного g-фотона. Імовірність комптонівського розсіювання росте з ростом атомного номера Z і падає із ростом їх енергії:
Комптонівське розсіювання відбувається інтенсивніше на найбільш слабко зв'язаних електронах. Розсіяний g-квант може мати достатню енергію, щоб ще раз розсіятись чи здійснити фотоефект. Тому комптонівське розсіювання, як правило, супроводжується випромінюванням рентгенівських променів і електронів Оже, а також має місце інтенсивна іонізація. Порядок виконання роботи Лабораторна установка дає можливість визначити загальний коефіцієнт ослаблення g- променів у свинці. Для виконання цієї роботи слід одержати в лаборанта радіоактивний препарат Co60, який знаходиться в свинцевому контейнері, що має коліматорний отвір і свинцеві фільтри, товщина яких по 1 мм. При роботі з радіоактивним препаратом Co60 будьте уважними! 1. Виміряти інтенсивність g-променів, тобто число g-квантів без поглинальних фільтрів. Час випромінювання 1...2 хв. 2. На шляху проходження g-променів між препаратом і лічильником розмістити спочатку одну пластинку, потім дві і т.д., як поглинальні фільтри. Виміряти N(x). Час вимірювання 1...2 хв. Результати вимірювань занести до таблиці.
3. Побудувати графік залежності In N(x) = f(x). Підберіть масштаб для N(x) таким, щоб кут нахилу одержаної лінії до осі х складав не менше 30° рис. 6-3.2. 4. Користуючись графіком залежності lnN(x)=f(x), знайдіть коефіцієнт поглинання g-променів у свинці;
тобто коефіцієнт поглинання визначається як тангенс кута нахилу експериментальної лінії в області найбільшої прямолінійності. Для збільшення точності вимірювання не слід брати сусідні точки.
Рис. 6.3. 2 5. Користуючись графіками на рис. 6.3.1, знайти значення енергії g-квантів і коефіцієнтів ослаблення mф, mк, mп. Результати вимірювань записати у такому вигляді: m=mф+mк+mп 6. Зробити необхідні висновки про точність вимірювання.
Контрольні запитання 1. Природа g-випромінювання. 2. Як взаємодіють g- промені з речовиною? 3. Як можна зареєструвати g- випромінювання? 4. У чому полягає відмінність реєстрації g- випромінювання від інших видів випромінювання? 5. Де практично використовують м’яке та жорстке g- випромінювання? Лабораторна робота № 6.4 Мета роботи: ознайомитись з одним з методів реєстрації іонізуючого випромінювання – методом товстошарових фотоемульсійних пластинок. Прилади і матеріали: біологічний мікроскоп з препаратопереміщувачем; товстошарові фотоемульсійніпластинки з і слідами іонізуючого випромінювання. Теоретичні відомості Доки частинка летить у вакуумі і ні з чим не взаємодіє, її неможливо спостерігати. Частинку можна зареєструвати лише при взаємодії її з речовиною. Відомі різні види взаємодії частинки з речовиною. Заряджені частинки, проходячи через речовину, викликають іонізацію і збудження атомів середовища, що, в свою чергу, може проявитись у вигляді помітних ефектів: імпульсів струму, спалахів світла і інше. Гамма-кванти самі не створюють іонізації, але, взаємодіючи з атомами середовища, вони можуть у результаті різноманітних ефектів породжувати швидкі електрони, які вже іонізують речовину. Нейтрони викликають різноманітні ядерні реакції, в ході яких виникають швидкі заряджені частинки: протони, Можливі процеси взаємодії частинок з речовиною і не позв'язана з іонізацією, наприклад, генерація квантів випромінювання Вавилова –Черенкова. Всі ці процеси, суть яких – перетворення енергії випромінювання в інші види енергії, можна використати для реєстрації частинок. До пристроїв, в яких безпосередньо використовується створювана випромінюванням іонізація речовини, відносяться іонізаційні камери, газорозрядні лічильники Гейгера, напівпровідникові детектори, камера Вільсона, фотоемульсії і інші. Зупинимось дещо детальніше на фотоемульсійному методі реєстрації заряджених частинок.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 485; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.79.70 (0.263 с.) |
 частинок за довжиною вільного пробігу в повітрі ………………….................................
частинок за довжиною вільного пробігу в повітрі ………………….................................
 випромі-нювання ……....................................................................................................
випромі-нювання ……....................................................................................................
 ..............................................
..............................................

 (1)
(1) – материнське ядро;
– материнське ядро; – дочірнє ядро;
– дочірнє ядро;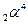 – a-частинка (ядро атома гелію);
– a-частинка (ядро атома гелію); – енергія, яка звільняється при a-розпаді (кінетична енергія a-частинки).
– енергія, яка звільняється при a-розпаді (кінетична енергія a-частинки). (рис. 6-1.1). Коли б не існувало потенціального бар’єра, a-частинки вилітали б з ядра, маючи при цьому енергію
(рис. 6-1.1). Коли б не існувало потенціального бар’єра, a-частинки вилітали б з ядра, маючи при цьому енергію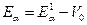 .
.
 , де показані різні енергетичні групи випромінювання a-частинок.
, де показані різні енергетичні групи випромінювання a-частинок. може перебувати як в основному стані, так і в двох збуджених станах.
може перебувати як в основному стані, так і в двох збуджених станах.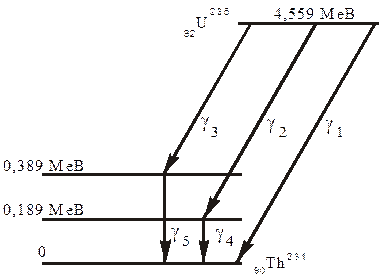
 , (3)
, (3)
 -випромінювання.
-випромінювання.
 . (1)
. (1) , (2)
, (2) . (3)
. (3) . (4)
. (4)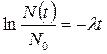 . (5)
. (5) . (6)
. (6) . (7)
. (7) ,
, , (8)
, (8) – середній час життя радіоактивного ядра.
– середній час життя радіоактивного ядра. . (9)
. (9) . (10)
. (10) ,
, — початкова активність препарату.
— початкова активність препарату. . (11)
. (11) ).
). ). Нейтрино і антинейтрино мають спін
). Нейтрино і антинейтрино мають спін 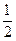 і рухаються подібно до g- кванта зі швидкістю світла, не маючи при цьому ні маси, ні заряду.
і рухаються подібно до g- кванта зі швидкістю світла, не маючи при цьому ні маси, ні заряду. . Вона залежить від енергії, яку при цьому має нейтрино, що і є головною причиною суцільного спектра b-частинок. В середньому разом з b- частинками звільняється енергія, яка дорівнює
. Вона залежить від енергії, яку при цьому має нейтрино, що і є головною причиною суцільного спектра b-частинок. В середньому разом з b- частинками звільняється енергія, яка дорівнює  .
.
 , (12)
, (12) , (13)
, (13) . (14)
. (14) ,
,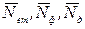 – середні значення імпульсів, які зафіксовані перерахунковим приладом за час t = 100 с.
– середні значення імпульсів, які зафіксовані перерахунковим приладом за час t = 100 с.
 .
.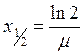 . (2)
. (2) . (3)
. (3) –кванта і енергією зв'язку даного електрона в атомі:
–кванта і енергією зв'язку даного електрона в атомі: , (6)
, (6) , (8)
, (8) . (9)
. (9)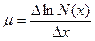 ,
,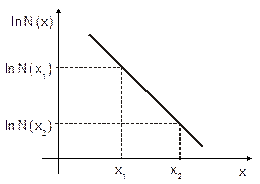
 -частинки, уламки атомних ядер та інші, або утворюються нестабільні ядра, які, як відомо, можна виявити за їх радіоактивністю.
-частинки, уламки атомних ядер та інші, або утворюються нестабільні ядра, які, як відомо, можна виявити за їх радіоактивністю.


