
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спонтанное и вынужденное излучение.
1.1.1. Спонтанное излучение (рис. 1.1, а)
Рассмотрим в некоторой среде два энергетических уровня 1 и 2 с энергиями Е1 и Е2 (Е1 < Е2). В последующем рассмотрении это могут быть любые два уровня из неограниченного набора уровней, свойственных данной среде. Однако удобно принять уровень 1 за основной. Предположим, что атом (или молекула) вещества находится первоначально в состоянии, соответствующем уровню 2. Поскольку Е1 < Е2, атом будет стремиться перейти на уровень 1. Следовательно, из атома должна выделиться соответствующая разность энергий Е2 — Е1. Когда эта энергия высвобождается в виде электромагнитной волны, процесс называют спонтанным излучением. При этом частота ν излученной волны определяется формулой (полученной Планком)
ν = (Е2 — Е1)/h, (1.1)
где h — постоянная Планка. Таким образом, спонтанное излучение характеризуется испусканием фотона с энергией hν = Е2 — Е1 при переходе атома с уровня 2 на уровень 1 (рис. 1.1, а). Заметим, что спонтанное излучение только один из двух возможных путей перехода атома из одного состояния в другое. Переход может происходить также и безызлучательным путем. В этом случае избыток энергии Е2 — Е1 выделяется в какой-либо иной форме (например, разность энергии может перейти в кинетическую энергию окружающих молекул). Вероятность спонтанного излучения можно определить следующим образом. Предположим, что в момент времени t на уровне 2 находятся N2 атомов (в единице объема). Скорость перехода (dN2/dt)спонт этих атомов вследствие спонтанного излучения на нижний уровень, очевидно, пропорциональна N2. Следовательно, можно написать
(dN2/dt)спонт =-АN2 (1.2)
Множитель А представляет собой вероятность спонтанного излучения и называется коэффициентом Эйнштейна А (выражение для А впервые было получено Энштейном из термодинамических соображений). Величину τ спонт = 1/А называют спонтанным временем жизни. Численное значение величины А зависит от конкретного перехода, участвующего в излучении.
Рис. 1.1. Схематическое представление трех процессов, а — спонтанное излучение; б — вынужденное излучение; в — поглощение.
1.1.2. Вынужденное излучение (рис. 1.1, б)
Предположим снова, что атом первоначально находится на верхнем уровне 2 и на вещество падает электромагнитная волна с частотой ν, определяемой выражением (1.1) (т. е. с частотой, равной частоте спонтанно испущенной волны). Поскольку частоты падающей волны и излучения, связанного с атомным переходом, равны друг другу, имеется конечная вероятность того, что падающая волна вызовет переход атома с уровня 2 на уровень 1. При этом разность энергий Е2 — Е1 выделится в виде электромагнитной волны, которая добавится к падающей. Это и есть явление вынужденного излучения. Между процессами спонтанного и вынужденного излучения имеется существенное отличие. В случае спонтанного излучения атом испускает электромагнитную волну, фаза которой не имеет определенной связи с фазой волны, излученной другим атомом. Более того, испущенная волна может иметь любое направление распространения. В случае же вынужденного излучения, поскольку процесс инициируется падающей волной, излучение любого атома добавляется к этой волне в той же фазе. Падающая волна определяет также направление распространения испущенной волны.
Процесс вынужденного излучения можно описать с помощью уравнения
(dN2/dt)вын =W21N2 (1.3)
где (dN2/dt)вын — скорость перехода 2 - 1 за счет вынужденного излучения, a W21 — вероятность вынужденного перехода. Вероятность W21, зависит не только от конкретного перехода, но и от интенсивности падающей электромагнитной волны. Точнее, для плоской волны, как будет показано ниже, можно написать
W21=σ2lF; (1.4)
здесь F — плотность потока фотонов в падающей волне, а σ2l— величина, имеющая размерность площади (она называется сечением вынужденного излучения) и зависящая от характеристик данного перехода.
1.1.3. Поглощение (рис. 1.1,в)
Предположим теперь, что атом первоначально находится на уровне 1. Если это основной уровень, то атом будет оставаться на нем до тех пор, пока на него не подействует какое-либо внешнее возмущение. Пусть на вещество падает электромагнитная волна с частотой v, определяемой выражением (1.1). В таком случае существует конечная вероятность того, что атом перейдет на верхний уровень 2. Разность энергий Е2 — Е1 необходимая для того, чтобы атом совершил переход, берется из энергии падающей электромагнитной волны. В этом заключается процесс поглощения.
По аналогии с (1.3) вероятность поглощения W12 определяется уравнением
(dN1/dt)вын =W12N1 (1.5)
где N1 — число атомов в единице объема, которые в данный момент времени находятся на уровне 1. Кроме того, так же, как и в выражении (1.4), можно написать
W12=σl2F; (1.6)
здесь σl2 — некоторая характерная площадь (сечение поглощения), которая зависит только от конкретного перехода. В предыдущих разделах были даны основные понятия процессов спонтанного и вынужденного излучений, а также поглощения. На языке фотонов эти процессы можно описать следующим образом (рис. 1.1): 1) в процессе спонтанного излучения атом, испуская фотон, переходит с уровня 2 на уровень 1; 2) в процессе вынужденного излучения падающий фотон вызывает переход 2-1, в результате чего мы получаем два фотона (падающий плюс испущенный); 3) в процессе поглощения падающий фотон поглощается, вызывая переход 1 - 2. Следует отметить, что σl2= σ2l, как показал Эйнштейн еще в начале XX в. Это означает, что вероятности вынужденного излучения и поглощения равны друг другу. Поэтому в дальнейшем мы будем писать σl2= σ2l = σ, понимая под а сечение данного перехода. Число атомов в единице объема, находящихся на данном энергетическом уровне, будем называть населенностью этого уровня.
Принцип работы лазера
Рассмотрим в какой-либо среде два произвольных энергетических уровня 1 и 2 с соответствующими населенностями N1 и N2. Пусть в этой среде в направлении оси z распространяется плоская волна с интенсивностью, соответствующей плотности потока фотонов F. Тогда в соответствии с выражениями (1.3) — (1.6) изменение плотности потока dF, обусловленное как процессами вынужденного излучения, так и процессами поглощения, в слое dz (заштрихованная область на рис. 1.2) определяется уравнением
dF=σF(N2 -. N1) (1.7)
Из уравнения (1.7) следует, что в случае N2 > N1 среда ведет себя как усиливающая (т. е. dF/dz > 0), а в случае N2 <. N1 — как поглощающая. Известно, что при термодинамическом равновесии населенности энергетических уровней описываются статистикой Больцмана. Так, если N2e и N1e — населенности двух уровней при термодинамическом равновесии, то мы имеем
N2e/N1e = exp[-(E2-E1)/kT], (1.8)
где k — постоянная Больцмана, а T — абсолютная температура среды. Таким образом, мы видим, что в случае термодинамического равновесия N2 <. N1. В соответствии с (1.7) среда поглощает излучение на частоте ν, что обычно и происходит. Однако если удастся достигнуть неравновесного состояния, для которого N2 >. N1, то среда будет действовать как усилитель. В этом случае будем говорить, что в среде существует инверсия населенностей, имея в виду, что разность населенностей (N2 -. N1> 0) противоположна по знаку той, которая существует в обычных условиях (N2 -. N1< 0). Среду, в которой осуществлена инверсия населенностей, будем называть активной средой. Если частота перехода ν = (Е2 — Е1)/h попадает в СВЧ-диапазон, то соответствующий усилитель называется мазером. Слово мазер (англ. maser) образовано из начальных букв слов следующей фразы: microwave amplification by stimulated emission of radiation — усиление микроволн вынужденным испусканием излучения. Если же частота перехода ν соответствует оптическому диапазону, то усилитель называется лазером. Слово лазер (англ. laser) образовано аналогично, только начальная буква «м», происходящая от первой буквы в слове microwave, заменена буквой «л», происходящей от слова light (свет).
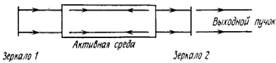
Для того чтобы усилитель превратить в генератор, необходимо ввести подходящую положительную обратную связь. В СВЧ-диапазоне это достигается тем, что активную среду помещают в объемный резонатор, имеющий резонанс при частоте ν. В лазере обратную связь обычно получают размещением активной среды между двумя зеркалами с высоким коэффициентом отражения (например, между плоскопараллельными зеркалами, как показано на рис. 1.3. Такая система зеркал обычно именуется резонатором Фабри-Перо оптическим резонатором или открытым резонатором). В этом случае плоская электромагнитная волна, распространяющаяся в направлении, перпендикулярном зеркалам, будет поочередно отражаться от них, усиливаясь при каждом прохождении через активную среду. Если одно из двух зеркал сделано частично прозрачным, то на выходе системы можно выделить пучок полезного излучения Однако как в мазерах, так и в лазерах генерация возможна лишь при выполнении некоторого порогового условия. Например, в лазере генерация начинается тогда, когда усиление активной среды компенсирует потери в нем (скажем, потери, обусловленные частичным выходом излучения из резонатора через зеркало). В соответствии с выражением (1.7) усиление излучения за один проход в активной среде (т. е. отношение выходной и входной плотностей потока фотонов) равно exp[σ(N2— N1)∙l], где l— длина активной среды. Если потери в резонаторе определяются только пропусканием зеркал, то порог генерации будет достигнут при выполнении условия
R1R2(2σ(N2— N1)∙l) >1 (1.9)
где R1 и R2— коэффициенты отражения зеркал по интенсивности. Это условие показывает, что порог достигается тогда, когда инверсия населенностей приближается к некоторому критическому значению, называемому критической инверсией и определяемому соотношением
(N2— N1)кр=-ln(R1R2)/2σl (1.10)
Как только достигнута критическая инверсия, генерация разовьется из спонтанного излучения. Действительно, фотоны, которые спонтанно испускаются вдоль оси резонатора, будут усиливаться. Этот механизм и лежит в основе лазерного генератора, называемого обычно просто лазером. Однако теперь слово лазер широко применяется к любому устройству, испускающему вынужденное излучение — будь то в дальнем или ближнем ИК-, УФ- и даже в рентгеновском диапазонах. В таких случаях мы будем говорить соответственно об инфракрасных, ультрафиолетовых и рентгеновских лазерах. Заметим также, что названия твердотельный, жидкостный и газовый лазер определяются агрегатным состоянием активной среды.
Схемы накачки
Рассмотрим задачу о том, каким образом в данной среде можно получить инверсию населенностей. На первый взгляд может показаться, что инверсию можно было бы создать при взаимодействии среды с достаточно сильной электромагнитной волной частоты v, определяемой выражением (1.1). Поскольку при термодинамическом равновесии уровень 1 заселен больше, чем уровень 2, поглощение преобладает над вынужденным излучением, т. е. под действием падающей волны происходит больше переходов 1 - 2, чем переходов 2-1, и можно надеяться осуществить таким путем инверсию населенностей. Однако нетрудно заметить, что такой механизм работать не будет (по крайней мере в стационарных условиях). Когда наступят условия, при которых населенности уровней окажутся одинаковыми (N2=N1), процессы вынужденного излучения и поглощения начнут компенсировать друг друга и в соответствии с (1.7) среда станет прозрачной. В такой ситуации обычно говорят о двухуровневом насыщении.
Рис. 1.4. Трехуровневая (а) и четырехуровневая (б) схемы лазера.
Таким образом, используя только два уровня, невозможно получить инверсию населенностей. Естественно, возникает вопрос: можно ли это осуществить с использованием более чем двух уровней из неограниченного набора состояний данной атомной системы? Мы увидим, что в этом случае ответ будет утвердительным и можно будет соответственно говорить о трех и четырехуровневых лазерах в зависимости от числа рабочих уровней (рис. 1.4). В трехуровневом лазере (рис. 1.4, а) атомы каким-либо способом переводятся с основного уровня 1 на уровень 3. Если выбрана среда, в которой атом, оказавшийся в возбужденном состоянии на уровне 3, быстро переходит на уровень 2, то в такой среде можно получить инверсию населенностей между уровнями 2 и 1. В четырехуровневом лазере (рис. 1.4,6) атомы также переводятся с основного уровня (для удобства будем называть его нулевым) на уровень 3. Если после этого атомы быстро переходят на уровень 2, то между уровнями 2 и 1 может быть получена инверсия населенностей. Когда в таком четырехуровневом лазере возникает генерация, атомы в процессе вынужденного излучения переходят с уровня 2 на уровень 1. Поэтому для непрерывной работы четырехуровневого лазера необходимо, чтобы частицы, оказавшиеся на уровне 1, очень быстро переходили на нулевой уровень.
Мы показали, каким образом можно использовать три или четыре энергетических уровня какой-либо системы для получения инверсии населенностей. Будет ли система работать по трех- или четырехуровневой схеме (и будет ли она работать вообще!), зависит от того, насколько выполняются рассмотренные выше условия. Может возникнуть вопрос: зачем использовать четырехуровневую схему, если уже трехуровневая оказывается весьма эффективной для получения инверсии населенностей? Однако дело в том, что в четырехуровневом лазере инверсию получить гораздо легче. Чтобы убедиться в этом, прежде всего заметим, что разности энергий между рабочими уровнями лазера (рис. 1.4) обычно много больше, чем kT, и в соответствии со статистикой Больцмана [см., например, формулу (1.8)] почти все атомы при термодинамическом равновесии находятся в основном состоянии. Если мы теперь обозначим число атомов в единице объема среды как Nt, то в случае трехуровневой системы эти атомы первоначально будут находиться на уровне 1. Переведем теперь атомы с уровня 1 на уровень 3. Тогда с этого уровня атомы будут релаксировать с переходом на более низкий уровень 2. Если такая релаксация происходит достаточно быстро, то уровень 3 остается практически незаселенным. В этом случае, для того чтобы населенности уровней 1 и 2 сделать одинаковыми, на уровень 2 нужно перевести половину атомов Nt, расположенных первоначально на основном уровне. Инверсию населенностей будет создавать любой атом, переведенный на верхний уровень сверх этой половины от общего числа атомов. Однако в четырехуровневом лазере, поскольку уровень 1 первоначально был также незаселенным, любой атом, оказавшийся в возбужденном состоянии, будет давать вклад в инверсию населенностей. Эти простые рассуждения показывают, что по возможности следует искать активные среды, работающие по четырехуровневой схеме. Для получения инверсии населенностей возможно, разумеется, использование большего числа энергетических уровней. Процесс, под действием которого атомы переводятся с уровня 1 на уровень 3 (в трехуровневой схеме лазера), называется накачкой. Имеется несколько способов, с помощью которых можно реализовать этот процесс на практике, например при помощи некоторых видов ламп, дающих достаточно интенсивную световую волну, или посредством электрического разряда в активной среде.
Свойства лазерных пучков
Лазерное излучение характеризуется чрезвычайно высокой степенью монохроматичности, когерентности, направленности и яркости. К этим свойствам можно добавить генерацию световых импульсов малой длительности. Это свойство, возможно, менее фундаментально, но оно играет очень важную роль. Рассмотрим теперь эти свойства подробнее.
1.4.1. Когерентность.
Для любой электромагнитной волны можно определить два независимых понятия когерентности, а именно пространственную и временную когерентность. Для того чтобы определить пространственную когерентность, рассмотрим две точки P1 и Р2, выбранные с таким условием, что в момент времени t = 0 через них проходит волновой фронт некоторой электромагнитной волны, и пусть E1(t) и Е2(t) - соответствующие электрические поля в этих точках. Согласно нашему условию, в момент времени t = 0 разность фаз электрических полей в данных точках равна нулю. Если эта разность фаз остается равной нулю в любой момент времени t > 0, то говорят, что между двумя точками имеется полная когерентность. Если такое условие выполняется для любых пар точек волнового фронта, то данная волна характеризуется полной пространственной когерентностью. Практически для любой точки Р1, если мы имеем достаточную корреляцию фаз, точка Р2 должна располагаться внутри некоторой конечной области, включающей точку P1. В этом случае говорят, что волна характеризуется частичной пространственной когерентностью, причем для любой точки Р можно соответственно определить область когерентности. Для того чтобы определить временную когерентность, рассмотрим электрическое поле волны в данной точке Р в моменты времени t и t + τ. Если для данного интервала времени τ разность фаз колебаний поля остается одной и той же в любой момент времени t, то говорят, что существует временная когерентность на интервале времени τ. Если такое условие выполняется для любого значения τ, то волна характеризуется полной временной когерентностью. Если же это имеет место лишь для определенного интервала времени т, такого, что 0 < τ < τ0, то волна характеризуется частичной временной когерентностью с временем когерентности τ0. Представление о временной когерентности непосредственно связано с монохроматичностью. Электромагнитная волна с временем когерентности, равным τ0, имеет спектральную ширину Δν ~ 1/ τ0. В случае нестационарного пучка (например, лазерного пучка, полученного в результате модуляции добротности или синхронизации мод) время когерентности не связано обратно пропорциональной зависимостью с шириной полосы генерации и фактически может быть много больше, чем величина 1/ Δν. Следует заметить, что понятия временной и пространственной когерентности на самом деле не зависят друг от друга. Действительно, можно привести примеры волны, имеющей полную пространственную когерентность, но лишь частичную временную когерентность, и наоборот. Понятия пространственной и временной когерентности дают описание лазерной когерентности только в первом порядке.
Направленность
Это свойство является простым следствием того, что активная среда помещена в резонатор, например плоскопараллельный резонатор, показанный на рис. 1.3. В таком резонаторе могут поддерживаться только такие электромагнитные волны, которые распространяются вдоль оси резонатора или в очень близком к оси направлении. Для более глубокого понимания свойств направленности лазерных пучков (или в общем случае любой электромагнитной волны) удобно рассмотреть отдельно случаи, когда пучок обладает полной пространственной когерентностью и когда он имеет частичную пространственную когерентность. Рассмотрим вначале пучок с полной пространственной когерентностью. Даже в этом случае пучок с конечной апертурой неизбежно расходится вследствие дифракции. Пусть пучок с постоянной интенсивностью и плоским волновым фронтом падает на экран, в котором имеется отверстие диаметром D. Согласно принципу Гюйгенса волновой фронт в некоторой плоскости Р за экраном может быть получен путем суперпозиции элементарных волн, излученных каждой точкой отверстия. Из-за конечного размера D отверстия пучок имеет конечную расходимость θ. Ее значение можно вычислить с помощью теории дифракции. Для произвольного распределения амплитуды имеем
θ=βλ/D (1.11)
здесь λ — длина волны, a D — диаметр пучка. β— числовой коэффициент порядка единицы, значение которого зависит от формы распределения амплитуд и способа, каким определяются расходимость и диаметр пучка (для пучка с гауссовым распределением интенсивности по сечению, образующегося в одномодовом резонаторе β=0,61). Пучок, расходимость которого описывается выражением (1.11), называется дифракционно-ограниченным. Если волна имеет частичную пространственную когерентность, то ее расходимость будет больше, чем минимальное значение расходимости, обусловленное дифракцией. При соответствующих условиях работы выходной пучок лазера можно сделать дифракционно-ограниченным.
Яркость
Определим яркость какого-либо источника электромагнитных волн как мощность излучения, испускаемого с единицы поверхности источника в единичный телесный угол. Точнее говоря, рассмотрим элемент площади dS поверхности источника в точке О (рис. 1.7). Тогда мощность dP, излучаемая элементом поверхности dS в телесный угол dΩ в направлении 00', может быть записана следующим образом:
dP = BcosθdSdΩ (1.12)
здесь θ — угол между направлением 00' и нормалью к поверхности. Величина В зависит, как правило, от полярных координат θ и φ, т. е. от направления 00' и от положения точки О. Эта величина В на-зывается яркостью источника в точке О в направлении 00'. Яркость лазера даже небольшой мощности (например, несколько милливатт) на несколько порядков превосходит яркость обычных источников. Это свойство в основном является следствием высокой направленности лазерного пучка.
Импульсы малой длительности
При помощи специального метода, называемого синхронизацией мод, можно получить импульсы света, длительность которых приблизительно обратно пропорциональна ширине линии перехода 2-1. Например, в газовых лазерах, ширина линии усиления которых относительно узкая, можно получать импульсы излучения длительностью -—¦ 0,1 — 1 нс. Такие импульсы не рассматриваются как очень короткие, поскольку даже некоторые лампы-вспышки способны излучать световые импульсы длительностью менее 1 нс. Однако у твердотельных или жидкостных лазеров ширины линий усиления могут быть в 103— 105 раз больше, чем у газовых лазеров, и поэтому генерируемые ими импульсы оказываются значительно короче (от 1 пс до ~5 фс). Получение столь коротких импульсов света привело к новым возможностям в лазерных исследованиях и их применениях. Свойство генерации коротких импульсов, которое подразумевает концентрацию энергии во времени, в некотором смысле аналогично свойству монохроматичности, означающему концентрацию энергии в узком диапазоне длин волн. Однако генерация коротких импульсов является, по-видимому, менее фундаментальным свойством, чем монохроматичность. В то время как любой лазер можно в принципе изготовить таким, что он будет генерировать достаточно монохроматическое излучение, короткие импульсы можно получать лишь от лазеров с широкой линией излучения, т. е. на практике только от твердотельных или жидкостных лазеров. Газовые же лазеры, обладающие более узкими линиями усиления, лучше всего подходят для генерации высокомонохроматического излучения.
Ширина линии.
Однородное уширение.
Любые процессы, сокращающие время жизни частиц на уровнях, приводят к уширению линий соответствующих переходов. Действительно, определение энергии состояния должно проводиться за время, не превышающее время жизни в этом состоянии т. А тогда неточность определения энергии в соответствии с соотношением неопределенностей «энергия — время»
ΔЕΔt ≥ ђ (1.13)
не может быть меньше ђ /τ. Неопределенность энергии состояния приводит к неопределенности частоты перехода, равной 1/2πτ. Постоянная времени τ является мерой времени, необходимого для того, чтобы возбужденная система отдала свою энергию. Значение т определяется скоростями спонтанного излучения и безызлучательных релаксационных переходов. В отсутствие внешних воздействий спонтанное излучение определяет время жизни состояния. Поэтому наименьшая возможная, так называемая естественная ширина линии Δν0 определяется вероятностью спонтанного перехода А:
Δν0 =А/2π (1.14)
Естественная ширина, как правило, существенна только на очень высоких частотах (А ~ ν3) и для хорошо разрешенных переходов. Обычно влиянием спонтанного излучения на ширину линии можно пренебречь, так как в реальных условиях релаксационные переходы более эффективно сокращают время жизни. Как уже говорилось, в системах с дискретными уровнями энергии, кроме индуцированных и спонтанных переходов, существенную роль играют релаксационные безызлучательные переходы. Эти переходы возникают в результате взаимодействий квантовой частицы с ее окружением. Механизм процессов этих взаимодействий сильно зависит от вида конкретной системы. Это может быть взаимодействие между ионом и решеткой кристалла; это могут быть соударения между молекулами газа или жидкости и т. д. В конечном счете результатом действия релаксационных процессов является обмен энергией между подсистемой рассматриваемых частиц и тепловыми движениями во всей системе в целом, приводящий к термодинамическому равновесию между ними. Обычно время установления равновесия, время жизни частицы на уровне, обозначается Т 1и называется продольным временем релаксации. Такая терминология отвечает традиции, установившейся при исследовании явлений ядерного магнитного резонанса (ЯМР) и электронного парамагнитного резонанса (ЭПР). Продольная релаксация соответствует движению вектора высокочастотной намагниченности системы частиц вдоль направления внешнего постоянного магнитного поля. Существует еще поперечное время релаксации Т2, которое соответствует движению вектора намагниченности в плоскости, перпендикулярной направлению внешнего постоянного поля. Время Т 2является мерой того отрезка времени, в течение которого частицы приобретут случайные по отношению друг к другу фазы. Любой процесс, вносящий вклад во время релаксации Т2 т. е. любой процесс потери энергии частицами, приводит к потере фазы. Следовательно, Т2 < Т1. Так как время Т2 является самым коротким временем релаксации, то именно оно и определяет ширину линии перехода. Конечность времени жизни частицы в возбужденном энергетическом состоянии ведет к уширению уровней энергии. Излучение с уширенных уровней приобретает спектральную ширину. Наиболее общим, фундаментальным механизмом, ограничивающим сверху время жизни частицы на возбужденном уровне, является спонтанное излучение, которое должно, таким образом, иметь спектральную ширину, соответствующего скорости актов спонтанного распада. Квантовая электродинамика позволяет вычислить спектральное распределение квантов спонтанного излучения, исходящих с уровня шириной
ΔЕ = ђ /τ0. (1.15)
Контур линии спонтанного излучения оказывается имеющим так называемую лоренцеву форму с шириной
Δνл = ΔЕ / ђ = 1/2πτ0 (1.16).
Лоренцева форма линии определяется форм-фактором
q(ν)
и имеет вид резонансной кривой с максимумом на частоте ν =ν0, спадающей до уровня половины пиковой величины при частотах ν=ν0±Δνл/2. Очевидно, что полная ширина кривой на половине максимальной величины составляет Δνл. Если принимать во внимание возможность спонтанного распада не только верхнего из двух рассматриваемых уровней энергии, но и нижнего, когда нижний уровень не является основным, то под Δνл, входящей в формулу (1.17), следует понимать величину, определяемую суммой скоростей распада этих уровней
Δνл =1/2πτ01+1/2πτ02 (1.18)
Уширение линии, обусловленное конечностью времени жизни состояний, связанных рассматриваемым переходом, называется однородным. Каждый атом, находящийся в соответствующем состоянии, излучает при переходе сверху вниз линию с полной шириной Δνл и спектральной формой q(ν). Аналогично каждый атом, находящийся в соответствующем нижнем состоянии, поглощает при переходе снизу вверх излучение в спектре с полной шириной Δνл и в соответствии со спектральной зависимостью q(ν). Невозможно приписать какую-либо определенную спектральную компоненту в спектре q(ν) какому-то определенному атому. При однородном уширении вне зависимости от его природы спектральная зависимость q(ν)есть единая спектральная характеристика как одного атома, так и всей совокупности атомов. Изменение этой характеристики, в принципе возможное при том или ином воздействии на ансамбль атомов, происходит одновременно и одинаковым образом для всех атомов ансамбля. Примерами однородного уширения являются естественная ширина линии и столкновительное уширение в газах.
Неоднородное уширение.
Экспериментально наблюдаемые спектральные линии могут явиться бесструктурной суперпозицией нескольких спектрально неразрешимых однородно уширенных линий. В этих случаях каждая частица излучает или поглощает не в пределах всей экспериментально наблюдаемой линии. Такая спектральная линия называется неоднородно уширенной. Причиной неоднородного уширения может быть любой процесс, приводящий к различию в условиях излучения (поглощения) для части одинаковых атомов исследуемого ансамбля частиц, или наличие в ансамбле атомов с близкими, но различными спектральными свойствами (сверхтонкая структура того или иного вида), однородно уширенные спектральные линии которых перекрываются лишь частично. Термин «неоднородное уширение» возник в спектроскопии ЯМР, в которой уширение этого типа происходило из-за неоднородности внешнего намагничивающего поля в пределах исследуемого образца. Классическим примером неоднородного упшрения является доплеровское уширение, характерное для газов при малых давлениях и (или) высоких частотах. Атомы (молекулы, ионы) газа находятся в тепловом движении. Доплер-эффект первого порядка приводит к смещению частоты излучения частиц, летящих на наблюдателя со скоростью и, на величину ν0u/с, где ν0 — частота излучения покоящейся частицы, а с — скорость света. Естественное уширение превращает излучение на частоте ν0 в спектральную линию, но это уширение однородно, и частотный сдвиг ν0 и/с испытывает вся линия. Так как частицы газа движутся с различными скоростями, то частотные сдвиги их излучения различны, а суммарная форма линии газа в целом определяется распределением частиц по скоростям. Последнее верно, строго говоря, если естественная ширина линии много уже доплеровских сдвигов частоты, что, как правило, имеет место. Тогда, если обозначить через р(и) функцию распределения частиц по скоростям, форм-фактор доплеровской линии q(ν)оказывается связанным с р(и) простым соотношением:
q(ν)d ν= р(u)du (1.19)
Далее, наблюдаемая частота равна
ν = ν0 (1+u/с )). (1.20)
Следовательно, и = с( ν — ν0 )/ ν0 и du = c dν. При максвелловском распределении частиц по скоростям
где средняя тепловая скорость Здесь k — постоянная Больцмана, Т — температура газа, т — масса атома (молекулы) газа. Комбинируя (1.20) и (1.21), легко получить q(ν) в виде
где ΔνT=ν0u0/c - ширина спектральной линии. Линия, форма которой определяется форм-фактором (1.22), называется доплеровски уширенной линией. Ее форма описывается функцией Гаусса и симметрична относительно центральной частоты ν0. Спад кривой q(ν) (1.22) при сильной отстройке от ν0 происходит гораздо более круто, чем в случае лоренцева контура линии (1.17). Около центральной частоты гауссова кривая более полога. Очевидно, что ее ширина определяется параметром ΔνT. При удалении от центра кривой на ΔνT интенсивность падает в е раз.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.169.94 (0.105 с.) |



 (1.17)
(1.17)
 (1.21)
(1.21)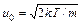
 , (1.22)
, (1.22)


