
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результати вимірювань та вихідні дані для розрахунку похибок
H =, прийнята довірча ймовірність a = 0.95, коефіцієнт Стьюдента t 0.95;5 = 2.8, dH =, vH =, dh =, vh = Обчислення похибок прямих вимірювань
Обчислити похибки прямих вимірювань величин H та h, враховуючи випадкову похибку (тільки для h), інструментальну похибку та похибку відліку. Результати вимірювання H і h записати в стандартній формі.
Обчислення похибки непрямого вимірювання Виведемо формулу для розрахунку відносної похибки непрямого вимірювання величини g: Для цього необхідно: а)обчислити середнє значення величини g: б) записати натуральний логарифм функції
в) знайти часткові похідні від функції ln g за змінними H і h:
г) записати формулу для відносної похибки непрямого вимірювання g:
Абсолютна похибка непрямого вимірювання величини g визначається за формулою:
Кінцевий результат непрямого вимірювання величини γ представити у стандартній формі:
Вважаючи повітря двохатомним газом, обчислити теоретичне значення величини gт за формулою: Порівняти отримане експериментальне відношення питомих теплоємностей повітря з розрахованим теоретичним значенням.
Питання для самоперевірки
1. Який газ називається ідеальним? Записати рівняння стану ідеального газу. 2. Дати визначення адіабатичному процесу. Записати рівняння Пуассона. 3. Записати і сформулювати перший принцип термодинаміки. 4. Що називається кількістю ступенів вільності руху молекули? 5. Скільки ступенів вільності руху використовують для характеристики повітря? Відповідь пояснити. 6. Дати визначення питомій та молярній теплоємності. Пояснити зв’язок між ними. 7. Чому молярна теплоємність при сталому тиску Cp завжди більша за молярну теплоємність при сталому об’ємі C v? 8. Чому в лабораторній роботі для визначення тиску необхідно зачекати декілька хвилин після випускання надлишку повітря з балону? 9. Як і чому змінюється з часом тиск у закритому балоні після того, як надлишок повітря з нього було випущено? 10. Як для газу теоретично розрахувати показник адіабати γ?
Лабораторна робота № 6
ВИЗНАЧЕННЯ КОЕФІЦІЄНТА В’ЯЗКОСТІ РІДИНИ МЕТОДОМ ПАДАЮЧОЇ КУЛЬКИ
Мета роботи: визначити коефіцієнт в’язкості рідини методом Стокса. Прилади і обладнання: скляна циліндрична посудина з в’язкою рідиною, металевий дріб, секундомір, мікрометр, масштабна лінійка, термометр.
Теоретичні відомості
При русі рідини між її шарами виникають сили внутрішнього тертя, що діють таким чином, щоб зрівняти швидкість усіх шарів. Природа цих сил полягає в тому, що шари, які рухаються з різними швидкостями, обмінюються молекулами. Молекули з більш швидкого шару передають більш повільному деяку кількість руху, внаслідок чого останній починає рухатися швидше. Молекули з більш повільного шару одержують у швидкому шарі деяку кількість руху і швидкий шар гальмується.
Рис. 1.
Розглянемо рідину, що рухається в напрямі осі ОХ (рис.1). Два шари рідини рухаються з різними швидкостями уздовж осі ОХ. На осі ОУ візьмемо дві точки М та N, що знаходяться на відстані Dу. Швидкості потоку в точках М та N відрізняються на
Сила внутрішнього тертя (в'язкості) діє між двома шарами, вона пропорційна площі їх зіткнення і градієнту швидкості:
Величина h називається коефіцієнтом внутрішнього тертя або коефіцієнтом динамічної в'язкості. Якщо вважати, що
Поряд з коефіцієнтом динамічної в'язкості h часто використовується коефіцієнт кінематичної в'язкості
де r – густина рідини. На тверду кульку, яка падає у в’язкій рідини, діють три сили: виштовхуюча сила за законом Архімеда, вага тіла і сила опору, обумовлена в'язкістю (внутрішнім тертям) рідини. Падаюча кулька змочується рідиною, при цьому найближчий (граничний) до поверхні кульки шар рідини буде рухатися зі швидкістю кульки. З віддаленням від кульки швидкість шарів рідини зменшується до нуля.
За умови повільного руху кульки в широкій посудині з рідиною сила опору рідини визначається за формулою, що була отримана Стоксом:
де h – коефіцієнт в'язкості;
d – діаметр кульки. Зі зростанням швидкості За умови рівномірного руху кульки в рідині має місце рівняння:
де r – густина тіла (металева кулька, сталь, свинець); r' – густина середовища (технічний гліцерин, касторова олія); g – прискорення вільного падіння. Швидкість рівномірного руху кульки
тоді остаточно:
Порядок виконання роботи
Рис. 2.
Прилад являє собою вертикально розташований скляний циліндр, який наповнено досліджуваною рідиною і має зовнішню шкалу (рис.2). По шкалі визначається відрізок шляху l рівномірного падіння кульки, час руху t якого вимірюється секундоміром. Перед опусканням кульки в рідину необхідно декілька разів виміряти діаметр кульки мікрометром. За допомогою пінцета занурити кульку в рідину вздовж осі циліндра. Відлік часу починати тоді, коли кулька знаходиться навпроти обраної верхньої мітки шкали „m”. Обрана верхня мітка повинна бути розташована на 5-6 см нижче рівня рідини. У момент проходження кульки через верхню мітку включити секундомір. При проходженні кульки через нижню обрану мітку „n” секундомір зупинити. У такий спосіб визначається час t проходження кулькою шляху l при рівномірному русі кульки. Результати вимірювань і обчислень занести до таблиці 1. Таблиця 1
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.181.231 (0.01 с.) |


 ;
;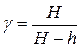 :
: ;
; ,
,  ;
;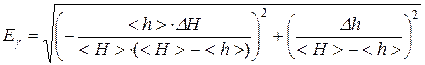 .
. .
. , для a = 0.95 та
, для a = 0.95 та  .
. .
.
 . Відношення
. Відношення  називається градієнтом швидкості і характеризує зміну швидкості потоку в напрямі осі OY.
називається градієнтом швидкості і характеризує зміну швидкості потоку в напрямі осі OY. . (1)
. (1) та DS = 1, то
та DS = 1, то  , тобто коефіцієнт динамічної в'язкості чисельно дорівнює силі внутрішнього тертя, що виникає на кожній одиниці поверхні зіткнення двох шарів, які рухаються один відносно іншого з градієнтом швидкості, рівним одиниці:
, тобто коефіцієнт динамічної в'язкості чисельно дорівнює силі внутрішнього тертя, що виникає на кожній одиниці поверхні зіткнення двох шарів, які рухаються один відносно іншого з градієнтом швидкості, рівним одиниці:
 .
.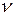 :
: . (2)
. (2) 
 , (3)
, (3) – швидкість руху кульки;
– швидкість руху кульки; .
. ,
, , (4)
, (4) , (5)
, (5) ,
, . (6)
. (6)



