
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составление структурной схемы исследуемой САУ
Из принципиальной схемы САР напряжения генератора получим функциональную схему. Начинать построение функциональной схемы рекомендуется с сумматора, который в принципиальной схеме представлен частью электрической схемы, предназначенной для сравнения сигналов Uзд и Uг. Полученный в соответствии с формулой (2) сигнал рассогласования ∆U поступает далее по цепочке – ЭУ, Д, Р и т.д. Выходной сигнал генератора по цепи отрицательной обратной связи поступает на сумматор.
Из функциональной схемы видно, что исходная САР напряжения генератора представляет собой замкнутую систему с отрицательной единичной обратной связью. Структурная схема легко получается из функциональной. Для этого в последней каждому функциональному элементу системы нужно поставить в соответствие его математическое описание в виде дифференциального уравнения, передаточной функции и т.п. Поэтому сначала получим математическое описание отдельных элементов системы.
Составление дифференциального уравнения отдельных элементов и расчет их передаточных функций. Электронный усилитель. Электронный усилитель предназначен для усиления сигнала по напряжению. Обозначив через ∆U входное напряжение усилителя, а через UЭУ – выходное, можно записать уравнение рассматриваемого звена UЭУ(t)=kэу ∆U(t). Передаточная функция усилителя
Здесь kэу – коэффициент усиления электронного усилителя. [1, стр.40] Двигатель. Передаточная функция двигателя постоянного тока, выходной координатой которого является угол поворота вала, примет вид
а соответствующее дифференциальное уравнение
Редуктор. Редуктор предназначен для изменения угловой скорости вращения выходного вала и, в некоторых случаях, изменения направления вращения. Уравнение редуктора φр(t)=kр*φд(t). (9) Тогда передаточная функция редуктора Wр (p)= kр=1. [1, стр.40] (10)
Потенциометр П1. Uп1(t)= kп1*φр(t), (11) где kп1- коэффициент передачи (усиления) потенциометра, следовательно, передаточная функция потенциометра будет Wп1 (p)= kп1=1. [1, стр.39] (12)
Электромашинный усилитель. В автоматизированных приводах прокатных станов, моторных машинах, копировально-фрезерных автоматах и других типах следящих приводов в качестве усилителей мощности широкое применение получили электромашинные усилители (ЭМУ). Современные ЭМУ с поперечным полем имеют коэффициент усиления по мощности 1000÷500000. Отечественная промышленность выпускает ЭМУ мощностью от 30 Вт до 100 кВт.
Передаточная функция ЭМУ с поперечным полем дается выражением
отсюда получим дифференциальное уравнение ЭМУво временной области
Генератор. Генератор постоянного тока предназначен для усиления сигнала по току и по мощности. Дифференциальное уравнение генератора может быть представлено в виде
Переходя в Лапласову область, получим передаточную функцию генератора
Получим структурную схему системы:
Составление дифференциального уравнения разомкнутой системы. Расчет передаточных функций разомкнутой и замкнутой системы. Передаточная функция цепочки последовательно соединенных звеньев равна произведению передаточных функций этих звеньев.
Так как все звенья структурной схемы соединены последовательно, то чтобы найти, передаточную функцию разомкнутой системы определим произведением передаточных функций всех звеньев системы. Wрисх(p)=Wэу(p)* Wд(p)* Wр(p)* Wп1(p)* Wэму(p)* Wг(p);
Отсюда получим дифференциальное уравнение разомкнутой исходной системы:
Найдем передаточную функцию замкнутой исходной системы по формуле:
Определение добротности (общий коэффициент усиления) системы. Требуемый для обеспечения заданной точности ∆=2,4%=0,024 коэффициент усиления kтр определяется по формуле
Коэффициент kэу найдем через добротность системы: kтр =3,22*kэу
Подставим kэу в передаточную функцию разомкнутой (18) и замкнутой (19) исходной системы:
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.81.94 (0.011 с.) |
 Рис.5 Функциональная схема исходной системы.
Рис.5 Функциональная схема исходной системы.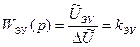 (6)
(6) , (7)
, (7) . [1, стр.38] (8)
. [1, стр.38] (8) ,т.к Тк=0, (13)
,т.к Тк=0, (13) [1, стр.42] (14)
[1, стр.42] (14) . (15)
. (15)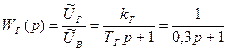 . [1, стр.41, 42] (16)
. [1, стр.41, 42] (16) Рис.6 Структурная схема исходной системы.
Рис.6 Структурная схема исходной системы. . [1, стр.44] (17)
. [1, стр.44] (17) (18)
(18)
 . (19)
. (19) [1, стр.163]
[1, стр.163]





