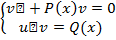Определение д.у. Порядок д.у. Общее и частное решение д.у.

1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию y = f(x) и ее производные yʹ, yʹʹ,… y⁽ⁿ⁾.Символическая запись ДУ: F=(yʹ, yʹʹ,…y⁽ⁿ⁾)=0.

Д.у.- ур-е в кот неизвестная ф-ция y нах под знаком производной (№: yʹ+5y=3x)

2. Порядком д.у. наз-ся порядок наивысшей производной, входящей в ур-е.

Если искомая функция у = f(x) есть функция одной независимой переменной, то ДУ называется обыкновенным ДУ (иначе ДУ называется ДУ в частных производных).

Решением или интегралом ДУ называется всякая дифференцируемая функция y = j(x), которая, будучи подставлена в уравнение, обращает его в тождество.

График решения ДУ (график функции у = f(x)) называется интегральной кривой.

Все д.у. делятся на 2 класса:

1)обыкновенные-ур-я в кот искомая неизв ф-ция y явл-ся функцией одного аргумента y=f(x)

2)д.у.в частных производных- -//- нескольких аргументов z=f(x,y)

3. Решением д.у. явл-ся любая ф-ция y= j (x), кот при подстановке в ур-е обращает его в строгое рав-во.

№: y=x³; yʹ=3x²

3y-xyʹ=0^; 3x³-x3x²=0; 0=0

Поскольку реш-е д.у связано с операцией интегрирования,то это приводит к появлению произвольной постоянной С.

При реш-и д.у. первого порядка появл-ся одна произвольная постоянная С.

-//- n-ного порядка интегрирование повторяется n раз, поэтому в реш-и будет содержаться n произв пост С С₁, С₂, С₃,… С_n,

Общим решением д.у. n-ого порядка называется функция: y= j (x, С₁, С₂, С₃,… С_n), кот зависит от n-произвольных постоянных и удовл д.у. при любых значениях С₁, С₂, С₃,… С_n,

Частным реш-ем д.у. n-ого порядка называется любая функция, полученная из общего решения д.у. при конкретных значениях произвольных постоянных.

Для нахождения частного из общего необх исп заданные заранее начальные усл-я.

№: нач усл-я: при х=х₀→у=у₀, yʹ= у₀ʹ, yʹʹ= у₀ʹʹ

y⁽ⁿ⁾- порядок производной

yⁿ -степень

 

 

Задача КОШИ. Теорема о существовании и единственности решения задачи Коши.

Задача отыскивания частного решения д.у. наз-ся решением задачи Коши.

Геометрически общее решение д.у. предст собой семейство кривых, кот назыв ИНТЕГРАЛЬНЫМИ КРИВЫМИ

y₀

x₀

Частное решение предст собой одну интегр кривую, прох через точку, заданную начальным условием.

Замечание. Решение ДУ, которое не может быть получено из общего решения ни при каких начальных условиях, называется особым.

Решить (проинтегрировать) ДУ – значит найти его общее решение и/или частное решение, удовлетворяющее заданным начальным условиям.

Геометрический смысл теоремы Коши. Существует, и притом единственная функция yʹ=j(x), график которой проходит через заданную точку (х ₀, у ₀) (единственная интегральная кривая, проходящая через заданную точку).

 

Рассмотрим решение простейшего ДУ первого порядка yʹ=f(x)

Решение такого уравнения сводится к интегрированию функции, стоящей в правой части уравнения

y=∫ f(x)dx+C

Пример. Общее решение дифференциального уравнения

y¢ – 3y = 0 имеет вид y(x) = Ce^3x. Найти его частное решение, удовлетворяющее начальным условиям y(1) = e³.

Решение.

Значение произвольной постоянной С, соответствующее искомому частному решению, получается в результате подстановки в общее решение заданных начальных условий: e³ = C×e³, откуда С = 1. Подставляя полученное значение С = 1 в общее решение, найдем частное решение y = e^3x, удовлетворяющее заданным начальным условиям.

 

 

ДУ первого порядка: определение, типы, общее и частное решения.

Д.у.- ур-е в кот неизвестная ф-ция y нах под знаком производной (№: yʹ+5y=3x)

ДУ первого порядка – уравнение вида: F(x,y, yʹ)=0 где х – независимая переменная; у – искомая функция; у¢ – ее производная.

Решением д.у. первого порядка назыв функция y=j(x,С) зависящая от одной произвольной постоянной С и кот при подстановке в ДУ обращает его в верное равенство. (и удовлетворяющая ДУ при любом конкретном значении С)

Частным реш-ем ДУ первого порядка является функция y=j(x,С₀) получаемая из общего решения при конкретном значении произвольной постоянной.

Соотношение вида Ф(х,у,С)=0 называется частным интегралом ДУ первого порядка.

Если ДУ первого порядка разрешено относительно производной yʹ=f(x,у), оно называется ДУ решенным относительно производной.

Другие формы записи ДУ первого порядка: dy/dx= f(x,у), P(x,y)dx+ Q(x,y)dy=0

Равенство вида Ф(х,у,С)=0 неявно задающее общее решение ДУ, называется общим интегралом ДУ.

Решение ДУ в виде общего интеграла получают, когда выразить у из соотношения Ф(х,у,С)=0 в элементарных функциях не представляется возможным.

Однородные ДУ первого порядка

О. Уравнение первого порядка yʹ=f(x,у), называется однородным относительно x и y, если функцию f(x,у) можно представить как функцию отношения y/х, т.е. в виде f(x,у)=j(y/х),

Существует еще один признак однородного уравнения. Если уравнение yʹ=f(x,у) или уравнение P(x,y)dx+ Q(x,y)dy=0 не меняется при замене x на λx и у на λу, то такие уравнения называются однородными.

Подстановка y/х=t→y=tx→ yʹ=tʹx+t приводит однородное уравнение к уравнению с разделяющимися переменными: tʹx+t=j(t)

Разделив переменные, получим: dt/(j(t)-t)=dx/х

Интегрируя последнее уравнение, найдем: ∫dt/(j(t)-t)=∫dx/х

Подставляя после интегрирования вместо t отношение у/х, получим интеграл уравнения.

 

Линейные ДУ первого порядка

1.О. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции y и ее производной yʹ, т.е. уравнение вида:

yʹ+ P(x) ×y=Q(x),

где P(x) и Q(x) – заданные непрерывные функции от х (или постоянные).

Если правая часть данного ур-я =0, т.е. Q(x) =0, то такое ДУ yʹ+ P(x) ×y=0 называется однородным линейным ДУ первого порядка.

yʹ+ P(x) ×y=Q(x) - неоднородное ЛДУ первого порядка

Линейным данное ур-е называется потому что искомая функция у и ее производная yʹ входят в первую степень и не содержат членов содержащих y×yʹ

Решение ЛДУ 1ого порядка.

2.1.Метод вариации произвольной постоянной (метод Лагранжа)

Последовательность решения ЛНДУ методом Лагранжа заключ в следующем:

В начале решается соответствующее исходному неоднородному ДУ однородное ДУ

yʹ+ P(x) ×y=0

dy/dx=- P(x) ×y |×dx |:y

∫dy/y=- ∫P(x) ×dx

ln|y|=-lne ^{P(x) ×dx}+ln|C|

|y|=| C×e^{-∫ P(x) ×dx}|

y= ±C×e^{-∫ P(x) ×dx} ±C=C₁

y= C₁×e^{-∫ P(x) ×dx}

с этого момента начинается вариация произвольной С₁

С₁=С₁(х) -т.к. С₁-любое значение

Тогда: y= C₁(х)×e^{-∫ P(x) ×dx}

Будем полагать что данное решение является решением иходного неоднородного ДУ, подставим его в yʹ+ P(x) ×y=Q(x) и определим закон изм-я произв постоянной С₁(х).

Для этого найдем производную yʹ

yʹ=производная первого на второе+производная второго на первое(y= C₁(х)×e^{-∫ P(x) ×dx})

yʹ= C₁ʹ(х)×e^{-∫ P(x) ×dx}- C₁(х)×Р(х)×e^{-∫ P(x) ×dx}

подставим полученные выражения в yʹ+ P(x) ×y=Q(x)

yʹ= C₁ʹ(х)×e^{-∫ P(x) ×dx}- C₁(х)×Р(х)×e^{-∫ P(x) ×dx}

y= C₁(х)×e^{-∫ P(x) ×dx}, тогда:

C₁ʹ(х)×e^{-∫ P(x) ×dx}- C₁(х)×Р(х)×e^{-∫ P(x) ×dx}+ P(x)×C₁(х)×e^{-∫ P(x) ×dx} =Q(x)

C₁ʹ(х)×e^{-∫ P(x) ×dx}=Q(x) |× e^{∫P(x) ×dx}

C₁ʹ(х)= Q(x)× e^{∫P(x) ×dx}

d C₁(х)/dx= Q(x)× e^{∫P(x) ×dx} |×dx

∫d C₁(х)= ∫Q(x)× e^{∫P(x) ×dx}×dx

C₁(х)= ∫Q(x)× e^{∫P(x) ×dx}×dx +C₂

Подставим полученное выражение в выражение y= C₁×e^{-∫ P(x) ×dx}

y=(∫Q(x)× e^{∫P(x) ×dx}×dx +C₂)×e^{-∫ P(x) ×dx}

пример:

1) уʹ+3у=е^2х

1. уʹ+3у=0

у=С₁×е^-3х (это реши сам)

2. пусть С₁ изм по вариации С₁=С₁(х), тогда реш-е однородного ур-я можно записать в виде:

у=С₁(х)×е^-3х-будем полагать что это общее решение исходного неоднородного ду.

3. Подставим его в исходное неоднор ур-е и найдем закон изменения С₁(х).

уʹ= С₁ʹ(х)×е^-3х-3 С₁(х)×е^-3х

4. подставим значения у и уʹ в исходное:

С₁ʹ(х)×е^-3х-3 С₁(х)×е^-3х+3 С₁(х)×е^-3х=е^2х

С₁ʹ(х)×е^-3х=е^2х |×е^3х

С₁ʹ(х)= е^5х

5. Разделим переменные:

d C₁(х)/dx= е^5х |×dx

∫d C₁(х)= ∫ е^5х ×dx

C₁(х)=1/5 е^5х +С₂

6. Подставим значение C₁(х) в у=С₁(х)×е^-3х. получим:

у=(1/5 е^5х +С₂) ×е^-3х

 

Метод Якова-Бернулли

Будем искать решение уравнения yʹ+ P(x) ×y=Q(x) в виде произведения двух функций y=uv, где u=u(x), v=v(x)- непрерывные ф-ции

Подберем такие функции u=u(x) и v=v(x), чтобы их произведение удовлетворяло исходному уравнению, т.е. превращало бы его в тождество.

Подставим в уравнение y=uv, yʹ=uʹv+ uvʹ:

uʹv+ uvʹ+Р(х)uv= Q(x)

или

uʹv+ u(vʹ+Р(х)v)= Q(x)

Выберем функцию v такой, чтобы vʹ+Р(х)v=0 из чего автоматически следует, что uʹv= Q(x)

Эти два условия превращают уравнение в тождество, поэтому для решения уравнения достаточно решить простую систему двух дифференциальных уравнений с разделяющимися переменными:

Решая первое уравнение системы, найдем функцию v (при интегрировании будем считать С = 0).

Подставив во второе уравнение системы найденную функцию v=v(x), решим дифференциальное уравнение с разделяющимися переменными относительно u, общее решение которого u=u(x,С). Следовательно, искомое общее решение уравнения будет иметь вид: y=v(x) × u(x,С).

 

Замечание. В ряде случаев дифференциальное уравнение первого порядка является линейным не относительно у, а относительно х, т.е. имеет вид: dy/dx+ P(у) ×х= Q(x)

Для интегрирования такого уравнения используется описанный выше метод, где неизвестной функцией является х=х(у)