Интерполирование или интерполяция – это один из наиболее часто применяемых на практике методов приближения функций. Задача интерполирования ставится следующим образом.
Рассмотрим пространство  функций, определенных на отрезке
функций, определенных на отрезке  . Пусть в пространстве
. Пусть в пространстве  задана последовательность линейно независимых функций
задана последовательность линейно независимых функций  . Пусть также на отрезке
. Пусть также на отрезке  задана последовательность попарно неравных точек
задана последовательность попарно неравных точек  при
при  . Образуем линейную комбинацию
. Образуем линейную комбинацию  (1)
(1)
Линейную комбинацию вида (1) называют обобщенным многочленом по системе функций  .
.
Систему функций  называют системой Чебышева на отрезке
называют системой Чебышева на отрезке  , если любой нетривиальный обобщенный многочлен по этой системе обращается в нуль на отрезке
, если любой нетривиальный обобщенный многочлен по этой системе обращается в нуль на отрезке  не более чем в n точках.
не более чем в n точках.
В задаче интерполирования функцию  нужно приблизить обобщенным многочленом (1) так, чтобы значения функции и обобщенного многочлена совпадали в заданных точках:
нужно приблизить обобщенным многочленом (1) так, чтобы значения функции и обобщенного многочлена совпадали в заданных точках:
 . (2)
. (2)
Обобщенный многочлен  , удовлетворяющий условиям (2), называют интерполяционным обобщенным многочленом. При этом функцию
, удовлетворяющий условиям (2), называют интерполяционным обобщенным многочленом. При этом функцию  , для которой строится интерполяционный обобщенный многочлен, называют интерполируемой функцией, а точки
, для которой строится интерполяционный обобщенный многочлен, называют интерполируемой функцией, а точки  называют узлами интерполяции. Равенства (2) будем называть интерполяционными условиями.
называют узлами интерполяции. Равенства (2) будем называть интерполяционными условиями.
Теорема существования и единственности интерполяционного обобщенного многочлена. Для того чтобы для любой функции  при любых наборах попарно неравных узлов
при любых наборах попарно неравных узлов 
 существовал интерполяционный обобщенный многочлен по системе функций
существовал интерполяционный обобщенный многочлен по системе функций  , необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке
, необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке  . При этом интерполяционный обобщенный многочлен будет единственным.
. При этом интерполяционный обобщенный многочлен будет единственным.
Доказательство. Возьмём из (1) интерполяционные условия 


 (1)
(1)
Интерполяционные условия представляют собой систему линейных алгебраических уравнений относительно неизвестных коэффициентов 
 . Система (1) имеет решение при любых правых частях тогда и только тогда, когда ее определитель
. Система (1) имеет решение при любых правых частях тогда и только тогда, когда ее определитель  отличен от нуля.
отличен от нуля.
Докажем необходимость. Допустим противное:  при любых наборах попарно неравных узлов на отрезке
при любых наборах попарно неравных узлов на отрезке  , а система функций
, а система функций  не является системой Чебышева на этом отрезке. Тогда существует нетривиальный обобщенный многочлен
не является системой Чебышева на этом отрезке. Тогда существует нетривиальный обобщенный многочлен 
 , который обращается в нуль на
, который обращается в нуль на  более чем в n точках. Возьмем n+ 1 из них в качестве узлов
более чем в n точках. Возьмем n+ 1 из них в качестве узлов 
 . Следовательно,
. Следовательно, 
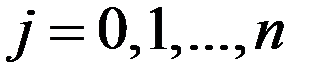 . Это означает, что столбцы определителя
. Это означает, что столбцы определителя  линейно зависимы и
линейно зависимы и  . Полученное противоречие доказывает необходимость.
. Полученное противоречие доказывает необходимость.
Достаточность. Допустим противное: система функций  является системой Чебышева на отрезке
является системой Чебышева на отрезке  , а
, а 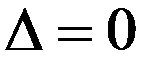 при некотором наборе попарно неравных узлов
при некотором наборе попарно неравных узлов 
 на этом отрезке. Следовательно, столбцы определителя линейно зависимы:
на этом отрезке. Следовательно, столбцы определителя линейно зависимы: 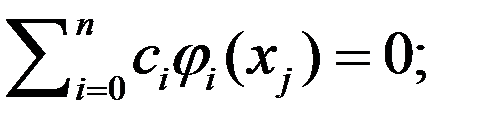
 . Последнее означает, что нетривиальный обобщенный многочлен
. Последнее означает, что нетривиальный обобщенный многочлен  обращается в нуль на
обращается в нуль на  более, чем в n точках, то есть, система функций
более, чем в n точках, то есть, система функций  не является на этом отрезке системой Чебышева. Полученное противоречие доказывает достаточность.
не является на этом отрезке системой Чебышева. Полученное противоречие доказывает достаточность.
Поскольку при  система (1) имеет единственное решение, то интерполяционный обобщенный многочлен также будет при этом единственным. Теорема доказана.
система (1) имеет единственное решение, то интерполяционный обобщенный многочлен также будет при этом единственным. Теорема доказана.
Интерполяционный многочлен Лагранжа.
Запишем решение с-мы 

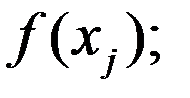
 (1) по ф-лам Крамера и выполним разложение
(1) по ф-лам Крамера и выполним разложение 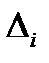 по столбцу i:
по столбцу i:  . Т.о., инт. об. мн-н м. представить в виде (2)
. Т.о., инт. об. мн-н м. представить в виде (2)




 .Интерполяционный многочлен Лагранжа. С-ма ф-ций
.Интерполяционный многочлен Лагранжа. С-ма ф-ций  , (1) в силу осн. теоремы алгебры, явл. с-мой Чебышева на любом отрезке. Для любой ф-ции
, (1) в силу осн. теоремы алгебры, явл. с-мой Чебышева на любом отрезке. Для любой ф-ции  по этой с-ме ф-ий при любом наборе попарно неравных узлов
по этой с-ме ф-ий при любом наборе попарно неравных узлов 
 ! инт. обоб. мн-н, к-ый м. б. записан в виде
! инт. обоб. мн-н, к-ый м. б. записан в виде  , (2) где обоб. мн-ны
, (2) где обоб. мн-ны  не зависят от ф-ии
не зависят от ф-ии  .Зафикс. j и рассм. ф-ию
.Зафикс. j и рассм. ф-ию  , приним. в узлах значения
, приним. в узлах значения  Для этой ф-ии имеем инт. обоб. мн-н
Для этой ф-ии имеем инт. обоб. мн-н  . Т.к. вып-ся инт. усл-я, то
. Т.к. вып-ся инт. усл-я, то  . Т.о., для обоб. мн-нов
. Т.о., для обоб. мн-нов  имеет место св-во
имеет место св-во  (3) Если построить обоб. мн-ны
(3) Если построить обоб. мн-ны  , удовл. св-ву (3), то тем самым б. построен инт. обоб. мн-н (2). Для с-мы ф-ий
, удовл. св-ву (3), то тем самым б. построен инт. обоб. мн-н (2). Для с-мы ф-ий 
 (1),очевидно, мн-ны
(1),очевидно, мн-ны  обл. св-м (3). Т.о., по с-ме ф-ий (3) инт-ый мн-н получается в виде
обл. св-м (3). Т.о., по с-ме ф-ий (3) инт-ый мн-н получается в виде  (4). (4) наз. инт.мн-м Лагранжа для ф-и
(4). (4) наз. инт.мн-м Лагранжа для ф-и  по
по  . Обозн.
. Обозн.  .имеем
.имеем 
 и
и  .С исп-ем мн-на
.С исп-ем мн-на  инт.мн-н Лагранжа примет вид
инт.мн-н Лагранжа примет вид  . (4’)
. (4’)
Схема Эйткина
Рассм. задачу инт-ия. Ф-я  задана на
задана на 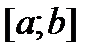 табл
табл  .(1) Треб. для заданного знач.
.(1) Треб. для заданного знач.  вычисл. приближ. знач. ф-и, исп-я инт. мн-н. Обозн. через
вычисл. приближ. знач. ф-и, исп-я инт. мн-н. Обозн. через 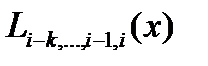 инт. мн-н, постр. для ф-и
инт. мн-н, постр. для ф-и  по узлам
по узлам  В сх. Эйткена сначала для заданного знач. арг.
В сх. Эйткена сначала для заданного знач. арг.  выб-ся ближ-й табл. узел среди всех табл-х узлов
выб-ся ближ-й табл. узел среди всех табл-х узлов  . Пусть это б. табл. узел
. Пусть это б. табл. узел  . Этот табл.узел берется в кач-ве узла инт-ии
. Этот табл.узел берется в кач-ве узла инт-ии  . Соотв.табл. зн-е ф-и
. Соотв.табл. зн-е ф-и  обозн.через
обозн.через 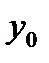 . Это табл.знач. м. сч. нач. приближением к иском. зн-ю ф-и в т.
. Это табл.знач. м. сч. нач. приближением к иском. зн-ю ф-и в т.  .Далее из ост. табл. узлов
.Далее из ост. табл. узлов  выбирается ближ. к
выбирается ближ. к  . Это б. или
. Это б. или  или
или  Найденный ближ. узел обозн.
Найденный ближ. узел обозн.  ,а соотв. табл. зн-е обозн.
,а соотв. табл. зн-е обозн.  Затем проводятся выч-я по ф-ле
Затем проводятся выч-я по ф-ле  .(2) Здесь в числителе дроби нах. определитель кв.матрицы 2-го порядка. Опр-мый ф-ой (2) мн-н
.(2) Здесь в числителе дроби нах. определитель кв.матрицы 2-го порядка. Опр-мый ф-ой (2) мн-н  имеет 1-ую степень и для него вып-ся инт. ус-я
имеет 1-ую степень и для него вып-ся инт. ус-я 
 . Б. сч. тожд-ми обоз-я
. Б. сч. тожд-ми обоз-я  и
и  Тогда ф-ла (2) м.б. переписана в виде
Тогда ф-ла (2) м.б. переписана в виде  . Выч-ое зн-е
. Выч-ое зн-е  явл. 2-ым приближением к искомому зн-ию
явл. 2-ым приближением к искомому зн-ию  . Это зн-е получается линейной инт-ей по ф-ле (2). На след. шаге сх.Эйткена из ост. табл. узлов
. Это зн-е получается линейной инт-ей по ф-ле (2). На след. шаге сх.Эйткена из ост. табл. узлов  нах. ближ. к заданному зн-ию
нах. ближ. к заданному зн-ию  и обозн. через (берется в качестве)
и обозн. через (берется в качестве)  . Новое приближение к искомому значению вычисляется по формуле
. Новое приближение к искомому значению вычисляется по формуле  (3) Перед этим предварительно должно быть вычислено
(3) Перед этим предварительно должно быть вычислено  , которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции
, которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции  ,
,  .Если значения
.Если значения  и
и  совпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение
совпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение  . В противном случае выбирается еще один узел интерполяции
. В противном случае выбирается еще один узел интерполяции  и проводятся вычисления по формуле
и проводятся вычисления по формуле  (4) при i=3 и k=1, 2, 3. Формула (4) является основной вычислительной формулой схемы Эйткена.
(4) при i=3 и k=1, 2, 3. Формула (4) является основной вычислительной формулой схемы Эйткена.


 функций, определенных на отрезке
функций, определенных на отрезке  . Пусть в пространстве
. Пусть в пространстве  . Пусть также на отрезке
. Пусть также на отрезке  задана последовательность попарно неравных точек
задана последовательность попарно неравных точек  при
при  . Образуем линейную комбинацию
. Образуем линейную комбинацию  (1)
(1) .
. называют системой Чебышева на отрезке
называют системой Чебышева на отрезке  нужно приблизить обобщенным многочленом (1) так, чтобы значения функции и обобщенного многочлена совпадали в заданных точках:
нужно приблизить обобщенным многочленом (1) так, чтобы значения функции и обобщенного многочлена совпадали в заданных точках: . (2)
. (2) , удовлетворяющий условиям (2), называют интерполяционным обобщенным многочленом. При этом функцию
, удовлетворяющий условиям (2), называют интерполяционным обобщенным многочленом. При этом функцию  , для которой строится интерполяционный обобщенный многочлен, называют интерполируемой функцией, а точки
, для которой строится интерполяционный обобщенный многочлен, называют интерполируемой функцией, а точки  называют узлами интерполяции. Равенства (2) будем называть интерполяционными условиями.
называют узлами интерполяции. Равенства (2) будем называть интерполяционными условиями. при любых наборах попарно неравных узлов
при любых наборах попарно неравных узлов 
 существовал интерполяционный обобщенный многочлен по системе функций
существовал интерполяционный обобщенный многочлен по системе функций  , необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке
, необходимо и достаточно, чтобы эта система функций была системой Чебышева на отрезке  . При этом интерполяционный обобщенный многочлен будет единственным.
. При этом интерполяционный обобщенный многочлен будет единственным.


 (1)
(1)
 . Система (1) имеет решение при любых правых частях тогда и только тогда, когда ее определитель
. Система (1) имеет решение при любых правых частях тогда и только тогда, когда ее определитель  отличен от нуля.
отличен от нуля. при любых наборах попарно неравных узлов на отрезке
при любых наборах попарно неравных узлов на отрезке  , а система функций
, а система функций  не является системой Чебышева на этом отрезке. Тогда существует нетривиальный обобщенный многочлен
не является системой Чебышева на этом отрезке. Тогда существует нетривиальный обобщенный многочлен 
 , который обращается в нуль на
, который обращается в нуль на  более чем в n точках. Возьмем n+ 1 из них в качестве узлов
более чем в n точках. Возьмем n+ 1 из них в качестве узлов 
 . Следовательно,
. Следовательно, 
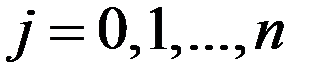 . Это означает, что столбцы определителя
. Это означает, что столбцы определителя  линейно зависимы и
линейно зависимы и  . Полученное противоречие доказывает необходимость.
. Полученное противоречие доказывает необходимость.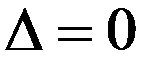 при некотором наборе попарно неравных узлов
при некотором наборе попарно неравных узлов 
 на этом отрезке. Следовательно, столбцы определителя линейно зависимы:
на этом отрезке. Следовательно, столбцы определителя линейно зависимы: 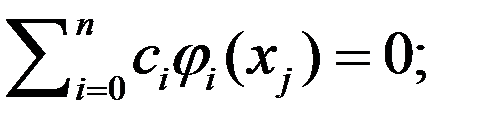
 . Последнее означает, что нетривиальный обобщенный многочлен
. Последнее означает, что нетривиальный обобщенный многочлен  обращается в нуль на
обращается в нуль на  система (1) имеет единственное решение, то интерполяционный обобщенный многочлен также будет при этом единственным. Теорема доказана.
система (1) имеет единственное решение, то интерполяционный обобщенный многочлен также будет при этом единственным. Теорема доказана.

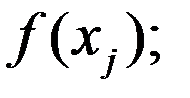
 (1) по ф-лам Крамера и выполним разложение
(1) по ф-лам Крамера и выполним разложение 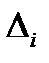 по столбцу i:
по столбцу i:  . Т.о., инт. об. мн-н м. представить в виде (2)
. Т.о., инт. об. мн-н м. представить в виде (2)



 .Интерполяционный многочлен Лагранжа. С-ма ф-ций
.Интерполяционный многочлен Лагранжа. С-ма ф-ций  , (1) в силу осн. теоремы алгебры, явл. с-мой Чебышева на любом отрезке. Для любой ф-ции
, (1) в силу осн. теоремы алгебры, явл. с-мой Чебышева на любом отрезке. Для любой ф-ции 
 ! инт. обоб. мн-н, к-ый м. б. записан в виде
! инт. обоб. мн-н, к-ый м. б. записан в виде  , (2) где обоб. мн-ны
, (2) где обоб. мн-ны  не зависят от ф-ии
не зависят от ф-ии  .Зафикс. j и рассм. ф-ию
.Зафикс. j и рассм. ф-ию  Для этой ф-ии имеем инт. обоб. мн-н
Для этой ф-ии имеем инт. обоб. мн-н  . Т.к. вып-ся инт. усл-я, то
. Т.к. вып-ся инт. усл-я, то  . Т.о., для обоб. мн-нов
. Т.о., для обоб. мн-нов  имеет место св-во
имеет место св-во  (3) Если построить обоб. мн-ны
(3) Если построить обоб. мн-ны 
 (1),очевидно, мн-ны
(1),очевидно, мн-ны  обл. св-м (3). Т.о., по с-ме ф-ий (3) инт-ый мн-н получается в виде
обл. св-м (3). Т.о., по с-ме ф-ий (3) инт-ый мн-н получается в виде  (4). (4) наз. инт.мн-м Лагранжа для ф-и
(4). (4) наз. инт.мн-м Лагранжа для ф-и  . Обозн.
. Обозн.  .имеем
.имеем 
 и
и  .С исп-ем мн-на
.С исп-ем мн-на  инт.мн-н Лагранжа примет вид
инт.мн-н Лагранжа примет вид  . (4’)
. (4’) задана на
задана на 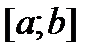 табл
табл  .(1) Треб. для заданного знач.
.(1) Треб. для заданного знач.  вычисл. приближ. знач. ф-и, исп-я инт. мн-н. Обозн. через
вычисл. приближ. знач. ф-и, исп-я инт. мн-н. Обозн. через 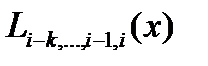 инт. мн-н, постр. для ф-и
инт. мн-н, постр. для ф-и  В сх. Эйткена сначала для заданного знач. арг.
В сх. Эйткена сначала для заданного знач. арг.  выб-ся ближ-й табл. узел среди всех табл-х узлов
выб-ся ближ-й табл. узел среди всех табл-х узлов  . Пусть это б. табл. узел
. Пусть это б. табл. узел  . Этот табл.узел берется в кач-ве узла инт-ии
. Этот табл.узел берется в кач-ве узла инт-ии  . Соотв.табл. зн-е ф-и
. Соотв.табл. зн-е ф-и  обозн.через
обозн.через 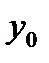 . Это табл.знач. м. сч. нач. приближением к иском. зн-ю ф-и в т.
. Это табл.знач. м. сч. нач. приближением к иском. зн-ю ф-и в т.  .Далее из ост. табл. узлов
.Далее из ост. табл. узлов  выбирается ближ. к
выбирается ближ. к  . Это б. или
. Это б. или  или
или  Найденный ближ. узел обозн.
Найденный ближ. узел обозн.  ,а соотв. табл. зн-е обозн.
,а соотв. табл. зн-е обозн.  Затем проводятся выч-я по ф-ле
Затем проводятся выч-я по ф-ле  .(2) Здесь в числителе дроби нах. определитель кв.матрицы 2-го порядка. Опр-мый ф-ой (2) мн-н
.(2) Здесь в числителе дроби нах. определитель кв.матрицы 2-го порядка. Опр-мый ф-ой (2) мн-н  имеет 1-ую степень и для него вып-ся инт. ус-я
имеет 1-ую степень и для него вып-ся инт. ус-я 
 . Б. сч. тожд-ми обоз-я
. Б. сч. тожд-ми обоз-я  и
и  Тогда ф-ла (2) м.б. переписана в виде
Тогда ф-ла (2) м.б. переписана в виде  . Выч-ое зн-е
. Выч-ое зн-е  явл. 2-ым приближением к искомому зн-ию
явл. 2-ым приближением к искомому зн-ию  . Это зн-е получается линейной инт-ей по ф-ле (2). На след. шаге сх.Эйткена из ост. табл. узлов
. Это зн-е получается линейной инт-ей по ф-ле (2). На след. шаге сх.Эйткена из ост. табл. узлов  нах. ближ. к заданному зн-ию
нах. ближ. к заданному зн-ию  и обозн. через (берется в качестве)
и обозн. через (берется в качестве)  . Новое приближение к искомому значению вычисляется по формуле
. Новое приближение к искомому значению вычисляется по формуле  (3) Перед этим предварительно должно быть вычислено
(3) Перед этим предварительно должно быть вычислено  , которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции
, которое вычисляется по формуле, аналогичной формуле (2), в которой все индексы должны быть увеличены на 1. Легко видеть, что при этом будут выполняться условия интерполяции  ,
,  .Если значения
.Если значения  и
и  совпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение
совпадают в пределах требуемой точности, то вычисления прекращаются. В качестве окончательного результата берется значение  . В противном случае выбирается еще один узел интерполяции
. В противном случае выбирается еще один узел интерполяции  и проводятся вычисления по формуле
и проводятся вычисления по формуле  (4) при i=3 и k=1, 2, 3. Формула (4) является основной вычислительной формулой схемы Эйткена.
(4) при i=3 и k=1, 2, 3. Формула (4) является основной вычислительной формулой схемы Эйткена.


