Вариация признака, характеристика размеров вариаций.

Вариацией признака называется различие численных значений признака у отдельных единиц совокупности

Число повторений отдельных вариантов называется частотой повторений. Для характеристики размера вариации используются специальные показатели колеблимости: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, коэффициент вариации.

Размах вариации- это разность между мах и мин значением признаков.R=xmax-xmin

Среднее линейное отклонение-это среднее арифметическое из абсолютных отклонений индивидуальных значений признака от среднего значения

Среднее линейное отклонение показывает на сколько в среднем отличается индивидуальное значение признака от их среднего значения. Среднее квадратическое отклонение представляет собой корень кВ. из среднего квадрата отклонений индивидуальных значений признака от средней арифметической

Очень часто в статистике возникает необходимость сравнения вариации различных признаков, в таких случаях используют показатель относительного рассеивания(коэффициент вариации)

К-ент вариации показывает на сколько % в среднем индивид. Значения отличаются от арифметических.

Число наблюдений обычно не велико и представляет собой выборку из исследуемой генеральной совокупности. С увеличением числа наблюдений и уменьшением величины интервала зигзаги полигона начинают сглаживаться и в приделах данных мы приходим к плавной кривой, которая называется кривой распределения.

Распределение бывает симметричным и ассиметричным.

 

18 Показатели динамики, их сущность, виды.
Динамика – развитие общественных явлений во времени.

Ряд статистических показателей, характеризующих это развитие – ряды динамики.

Каждый ряд состоит из 2-х граф. В одной указываются периоды или даты времени, во второй – числовая характеристика явления в эти периоды, называемая уровнем ряда.

Уровни ряда могут выражаться:

- абсолютными величинами

- средними

- относительными

Временные ряды, состоящие из абсолютных величин могут быть интервальные и моментные.

В интервальном ряду приводятся данные за период времени (сумма выручки, величина затрат…). Моментный ряд состоит из показателей, характеризующих явления на определенные моменты времени (величина остатков продукции на …, списочная численность, стоимость фонда). Данные интервальных рядов можно суммировать и получать новые значения с нарастающим итогом. Уровни моментных рядов складывать нельзя.

Для сравнения между собой отдельных уровней ряда динамики рассчитывают следующие показатели:

- абсолютные приросты (отклонения)

- темпы роста (коэффициенты роста)

- темпы прироста

- абсолютное значение 1 % прироста

При сравнении уровень, с которым оно осуществляется, может быть базисным или цепным.

а пер. = а1 – а0, а2 – а1, а3 – а2

а пост. = а1 – а баз., а2 – а баз., а3 – а баз.

Абсолютный прирост показывает на сколько в абсолютном выражении уровень отчетного периода больше или меньше уровня базисного периода.

Коэффициент роста показывает во сколько раз уровень отчетного периода больше или меньше уровня базисного

Может быть с переменной и постоянной базой сравнения

 

Коэффициент роста выраженный в % носит название темпа роста.

Коэффициенты роста, рассчитанные с переменной базой сравнения характеризуют изменение явления от периода к периоду, а с постоянной базой – непрерывную линию развития.

Темпы прироста показывают на сколько % уровень отчетного периода больше или меньше уровня базисного периода.

Для получения темпа прироста необходимо из величины темпа роста вычесть 100.

Абсолютное значение 1 % прироста

А 1 % = а0 / 100

Коэффициент роста, темп прироста и абсолютное значение 1% прироста характеризуют интенсивность процесса развития.

Для цели анализа достаточно часто возникает необходимость определения средних уровней ряда динамики, которые различаются в зависимости от вида ряда.

Для интервального ряда:

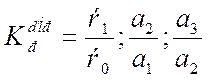
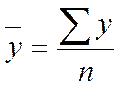(по средней арифметической простой), где n - число уровней ряда.