
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Государственное автономное профессиональноеСтр 1 из 3Следующая ⇒
Государственное автономное профессиональное образовательное учреждение «Оренбургский учетно-финансовый техникум»
Е. А. Кургина
СБОРНИК ОПОРНЫХ КОНСПЕКТОВ И ЗАДАЧ ПО МАТЕМАТИКЕ По теме: «Элементы теории комбинаторики, теории вероятностей»
Оренбург 2016
Сборник предназначен для студентов по специальности: 39.02.01 «Социальная работа», 40.02.01 «Право и организация социального обеспечения», 40.02.03 «Право и судебное администрирование» очной формы обучения и может быть использовано при подготовке к экзамену.
Рассмотрено на заседании ПЦК математических и естественнонаучных дисциплин Протокол № 6 от 28.01. 2016 г. Председатель ПЦК ______ Н.В. Борисова
Утверждено научно - методическим советом Протокол № ____ от ________________ 2016 г. Заместитель директора техникума по учебной дисциплине_________ Т.Н. Тарасова
Содержание
Пояснительная записка Комбинаторика - это раздел математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов данного множества. Теория вероятностей - раздел математики, изучающий общие устойчивые закономерности в массовых случайных явлениях и количественные оценки степени возможности появления или не появления этих случайных явлений.
Эти теории находят многочисленные приложения как в естественных, так и в гуманитарных науках (естествознание, статистика, кибернетика, филология, экономика, техника, и т.д.) Методическая разработка полностью соответствует учебной программе по дисциплине БД.03 «Математика», предназначенной для реализации государственных требований к минимуму содержания и уровню подготовки выпускников по специальности: 39.02.01 «Социальная работа», 40.02.01 «Право и организация социального обеспечения», 40.02.03 «Право и судебное администрирование» очной формы обучения Цель методической разработки - помочь учащимся освоить и закрепить фундаментальные понятия случайного события, случайной величины, условной вероятности, познакомить с теоремами сложения, умножения вероятностей, для выработки умений применения полученных знаний при решении конкретных задач. В разработке приведены примеры задач и их решения, а также примеры типичных задач для самостоятельного вычисления, для самоконтроля в методической разработке приведён тест.
Лекция №1 Лекция №2 Тема: Треугольник Паскаля. Формула бинома Ньютона. Треугольник Паскаля Свойство №3 используют при построении треугольника Паскаля. Определение: Эта таблица называется треугольником Паскаля, по имени известного французского математика Блеза Паскаля (1623-1662), исследовавшего его свойства. С С С С С 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 Определение: Для каждого натурального числа n и произвольных чисел a и b имеет место равенств: Равенство называется формулой бинома Ньютона, где Формула Ньютона обладает следующими свойствами: 1) В разложении двучлена(а+b)n в формуле содержится n+1 член. 2) Сумма степеней всех одночленов раны степени двучлена n. 3) Степень первого выражения одночлена в разложении убывает, начиная со степени двучлена и заканчивая нулевой. 4) Степень второго выражения одночлена в разложении возрастает, начиная с нулевой и заканчивая степенью двучлена. 5) Биноминальные коэффициенты совпадают с числом соответствующей строки треугольника Паскаля.
6) Сумма биноминальных коэффициентов разложения Задача №1: Представьте каждую степень двучлена в виде многочлена. (a +b)2 = а2 +2аb + 2b2 (а +b)3 = а3 +3а2b+3аb2 +b3 (с +а)4 = с4+ 4с3а +6с2а2 + 4са3 +а4 (с +а)5 = (с +а)6= (с +а)4 Практические задания по комбинаторике 1. Вычислить: а) б) в) г) д) е) 2 Представьте каждую степень двучлена в виде многочлена: а) (х +2у)2, б) (а- b)3, в) (а+1)3, г) (с+3а)4, д) (1- 2а)4, е) (х -2)5, ж) (х+у)6 з) (х - 1)7 3. На этаже четыре кабинета для проведения занятий: русского языка, математики, естествознания, английского. Сколькими способами можно распределить кабинеты на этаже? 4. В вашей группе в среду пять уроков: русский язык, литератур, математика, информатика, ЧКР. Сколько вариантов расписания можно составить? 4 Изменяя порядок слов: руки, мою, я, составьте всевозможные предложения. 5 При встрече 5 человек обменялись рукопожатиями. Сколько сделано рукопожатий? 6 Сколько существует способов выбора трёх ребят из 4-х желающих дежурить в столовой? 7 Сколько экзаменационных комиссий, состоящих из 3 человек, можно создать из 5 преподавателей? 8 Сколько различных четных трехзначных чисел, в каждом из которых все цифры различны, можно составить из цифр 1, 2, 3, 0? 9. Сколькими способами можно составить расписание на день из 4 различных уроков, если изучается 10 предметов? 10. Бригадир должен отправить на работу бригаду из 4 человек. Сколько бригад по 4 человека в каждой можно составить из 13 человек? 11.Сколько различных трехцветных флагов можно сделать, комбинируя синий, красный и белый цвета? 12 Сколько различных двузначных чисел можно составить из данных 5 цифр:1,2,3,4,5. Лекция №1 Лекция №2 Лекция №3 Тест 1. Каково максимальное значение вероятности суммыпротивоположных событий? а) 0,5; 6) 0,25; в) 1,0; г)0,64. 2. Чему равна вероятность достоверного события? а) 0,5; 6) 0; в) 1,0; г) 0,25. 3. Монета подбрасывается два раза. Какова вероятность выпадения "орла» один раз? а) 1,0; 6) 0; в) 0,25;. г) 0,5. 4. Монета была подброшена 10 раз. "Герб" выпал 4 раза. Какова относительная частота выпадения "герба"? а) 0; б) 0,4; в) 0,5; г) 0,6. 5. Консультационный пункт института получает пакеты с контрольными работами студентов из городов А, В и С. Вероятность получения пакета из города А равна 0,7, из города В - 0,2. Какова вероятность того, что очередной пакет будет получен из города С? а) 0,14; 6) 0,1; в) 0,86; г) 0,9. 6. Какова вероятность выигрыша хотя бы одной партии у равносильного противника в матче, состоящем из трех результативных партий? а) 0,875; 6)1; в) 0,375; г) 0,333. государственное автономное профессиональное образовательное учреждение «Оренбургский учетно-финансовый техникум»
Е. А. Кургина
СБОРНИК ОПОРНЫХ КОНСПЕКТОВ И ЗАДАЧ ПО МАТЕМАТИКЕ
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.198.43 (0.028 с.) |
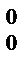
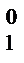 С
С 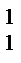
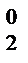 С
С 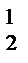 С
С 
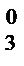 С
С 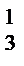 С
С 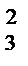 С
С 
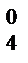 С
С 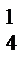 С
С  С
С 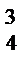 С
С 
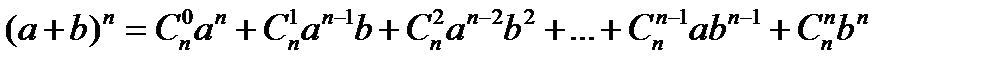
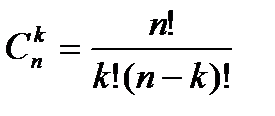 и
и 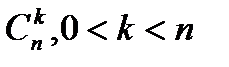 называют биномиальными коэффициентами.
называют биномиальными коэффициентами.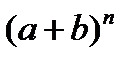 равна 2n
равна 2n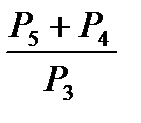 ;
;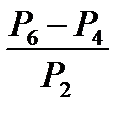 ;
; ;
; ;
; ;
; ;
;


