Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Замена эквиваленции и импликации на конъюнкцию, дизъюнкцию и отрицание. ⇐ ПредыдущаяСтр 5 из 5
До сих пор мы занимались равносильными преобразованиями формул, не содержащих знаков импликации “® “ и эквиваленции “«“. Сейчас покажем, что всякую формулу, содержащую “® “ или “«“, можно заменить равносильной ей формулой, не содержащей этих знаков.
Сравнивая колонки 3 и 5, 3 и 8, убеждаемся, что равносильности (1) и (2) имеют место. Эквиваленция выражается через конъюнкцию и импликацию: C «U º (C ® U) × (U ® C) (3) Вывод:
Вопросы и задания. 1. Формулы данных высказываний преобразовать в эквивалентные, исключив логическое сложение: 2. Формулы данных высказываний преобразовать в эквивалентные, исключив логическое умножение. 3. Упростить: 4. Записать данные высказывания, используя только операции логического умножения и отрицания. 5. Записать данные высказывания, используя только операции логического сложения и отрицания. 6. Упростить: 7. Данные высказывания преобразуйте в эквивалентные, но не содержащие отрицаний сложных высказываний: Логические основы построения ЭВМ В основе обработки компьютером информации лежит алгебра логики, разработанная Дж. Булем. Было доказано, что все электронные схемы ЭВМ могут быть реализованы с помощью логических элементов И, ИЛИ, НЕ.
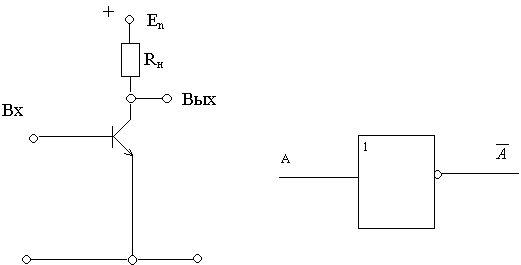
Элемент НЕ
При подаче на вход схемы сигнала низкого уровня (0) транзистор будет заперт, т.е. ток через него проходить не будет, и на выходе будет сигнал высокого уровня (1). Если же на вход схемы подать сигнал высокого уровня (1), то транзистор “откроется”, начнет пропускать электрический ток. На выходе за счет падения напряжения установится напряжение низкого уровня. Таким образом, схема преобразует сигналы одного уровня в другой, выполняя логическую функцию. Элемент ИЛИ
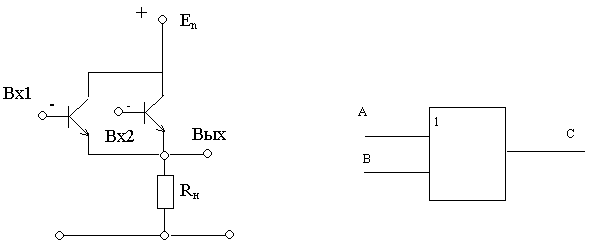
Функция “ИЛИ” - логическое сложение (дизъюнкция), ее результат равен 1, если хотя бы 1 из аргументов равен 1. Элемент И
Если на входы Вх1 и Вх2 поданы сигналы низкого уровня (логические “0”), то оба транзистора закрыты, ток через них не проходит, выходное напряжение на Rн близко к нулю.
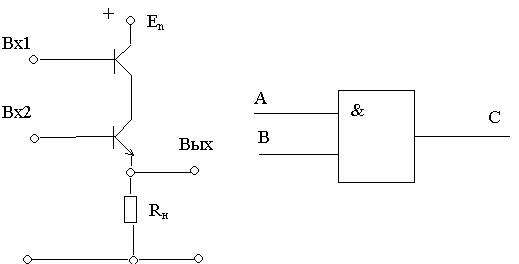
Структурные формулы и функциональные схемы логических устройств
Соответствующие схемы называются функциональными. Анализируя функциональную схему, можно понять, как работает логическое устройство, т.е. дать ответ на вопрос: какую функцию она выполняет.
Задание 1. Для каждой из функциональных схем выписать соответствующую структурную формулу.
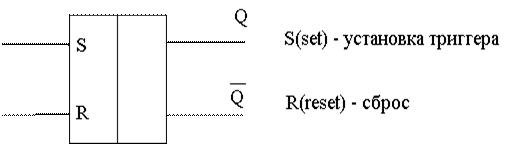
Триггер
Триггер - это элементарный цифровой автомат, имеющий два устойчивых состояния равновесия (0 и 1), предназначенный для записи и хранения информации.
Как он работает?
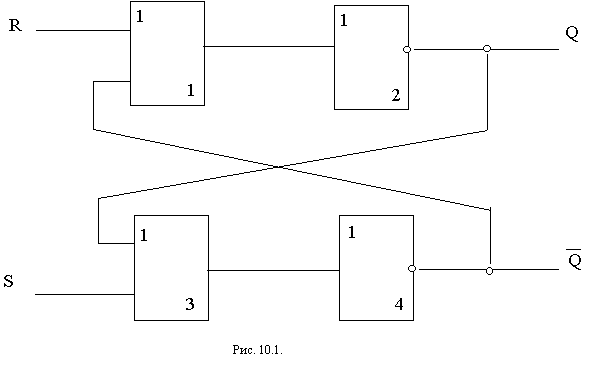
Таким образом, при отсутствии на внешних входах сигналов “1” триггер поддерживает постоянное напряжение на своих выходах. Чтобы изменить напряжение на выходах триггера, надо подать сигнал “1” на вход элемента № 3. Тогда Q=1,
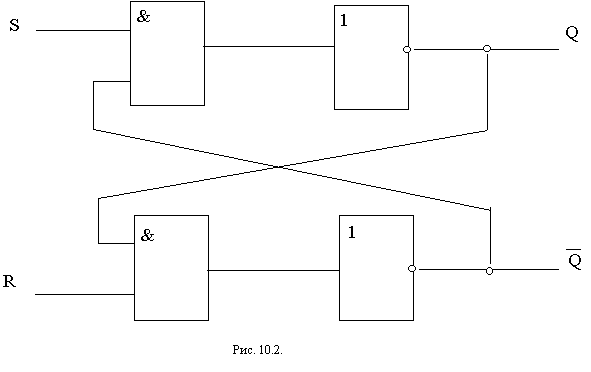
Cхема RS - триггера на элементах И - НЕ
Сумматор Узел ЭВМ выполняющий арифметическое суммирование кодов чисел, называется сумматором. Операция суммирования осуществляется в сумматорах поразрядно с использованием одноразрядных суммирующих схем. При этом в каждом разряде требуется выполнить сложение трех двоичных цифр данного разряда первого слагаемого Хi цифры этого же разряда второго слагаемого Yi и цифры переноса Pi из соседнего младшего разряда.
В таблице приведена логика работы сумматора на два входа X i и Yi. На его выходах образуется сумма Si данного разряда и осуществляется перенос Рi+1 в следующий старший разряд. По таблице можно составить логическое выражение для суммы Si и переноса Р i+1:
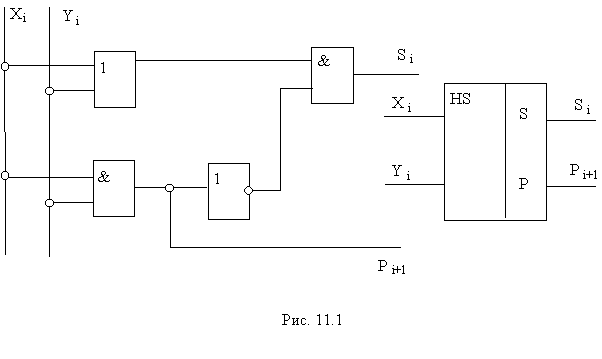
На рисунке 11.1 приведены функциональная схема полусумматора, составленная в соответствии с полученными логическими выражениями, и условное обозначение его. Схема является комбинационной и реализуется на логических элементах. Таблица А.
По таблице можно составить логические выражения:
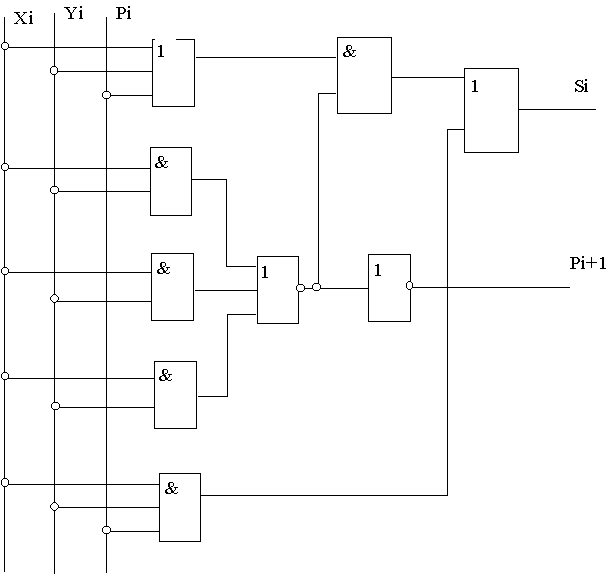
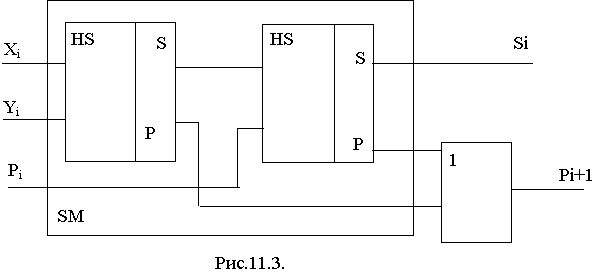
Комбинационный сумматор можно реализовать также с использованием двух полусумматоров и логического элемента ИЛИ, как показано на рис.11.3.
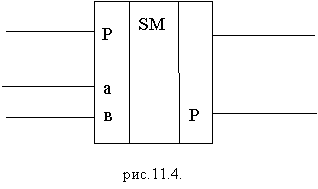
В реальных электронных схемах сумматор изображается так.
рис.11.5. Эта схема называется одноразрядным сумматором.
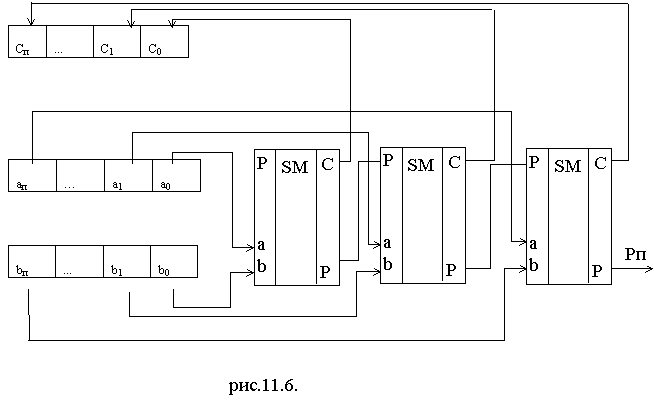
На рис.11.6. показано, как из N сумматоров можно составить устройство для сложения двух N-разрядных двоичных кодов, это схема многоразрядного сумматора.
Регистры
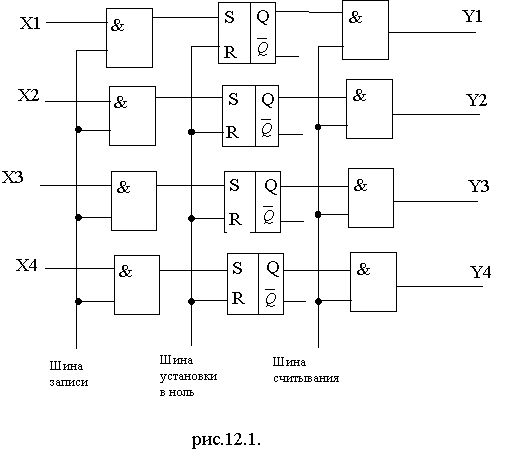
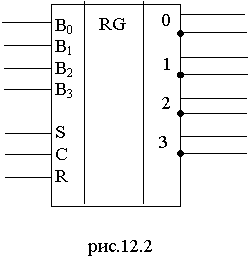
На рис.12.1. показана упрощенная схема регистра для записи чисел, имеющих 4 двоичных разряда.
В ЭВМ применяются регистры 8, 16, 32, 48 и 64 разрядов. Шифратор и дешифратор
Шифратор и дешифратор являются типовыми узлами ЭВМ. Таблица В.
На выходе Y0 еденица должна появиться при нажатии любой нечетной клавиши Х1, Х3, Х5, Х7, Х9, т.е. Y0=X1+X3+X5+X7+X9. Y1=X2+X3+X6+X7; Y2=X4+X5+X6+X7; Y3=X8+X9. Cледовательно, для реализации шифратора понадобится четыре элемента ИЛИ: пятивходовый, два четырех входовых и двухвходовый (рис.13.1.)
Дешифратор (декодер) - это узел, преобразующий код, поступающий на его входы, а сигнал только на одном из его выходов. Дешифраторы широко применяются в устройствах управления, в системах цифровой индикации с газоразрядными индикаторами, для построения распределителей импульсов по различным цепям и т.д. Схема используется я перевода двоичных цифр в десятичные. Дешифратор двоичного n-разрядного кода имеет 2n выходов, т.к. каждому из 2n значений входного кода должен соответствовать единичный сигнал на одном из выходов дешифратора. Таблица С.
Логические функции, описывающие работу такого дешифратора:
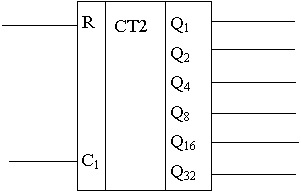
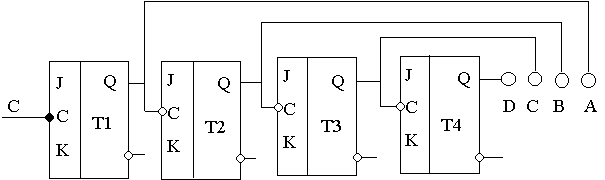
Счетчики Счетчики - устройства, регистрирующие число импульсов поступивших на вход. Цифры 1, 2, 4, 8, 16, 32 у Q показывают до какого значения может считать данная ступень счетчика. А общее число подсчитываемых счетчиком импульсов равно сумме чисел (1+2+4+8+16+32=63). 64-й импульс сбрасывает счетчик в начальное состояние. Рассмотрим схему счетчика по модулю 10, который считает импульсы от 0 до 9 (от 0000 до 1001).
Пусть в начальный момент состояния выходов счетчика соответствуют двоичному коду 0000 (счетчик очищен). При поступлении тактового импульса 1 на синхронный вход Т1.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1720; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.60.149 (0.044 с.) |
 (2)
(2) 
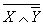 U
U 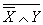 (5),
(5),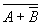 ; б)
; б) 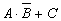 ; в)
; в) 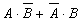 .
.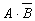 ; б)
; б) 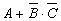 ; в)
; в) 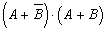 .
.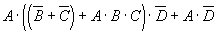 ; б)
; б) 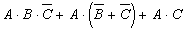 .
.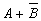 ; б)
; б)  ; в)
; в)  .
.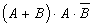 ; б)
; б) 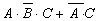 ; в)
; в) 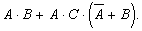
 ; б)
; б) 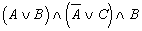 ; в)
; в) 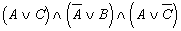 ;
;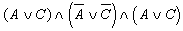 ; д)
; д) 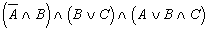 ;
; ; ж)
; ж) 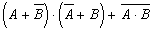 ;
; ; и)
; и) 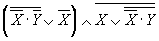 ;
;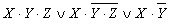 .
.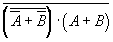 ; б)
; б) 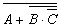 ; в)
; в)  .
.
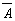
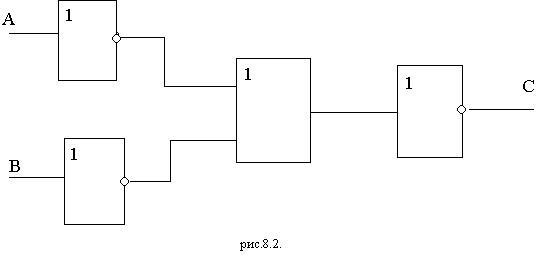

 и есть структурная формула логического устройства.
и есть структурная формула логического устройства.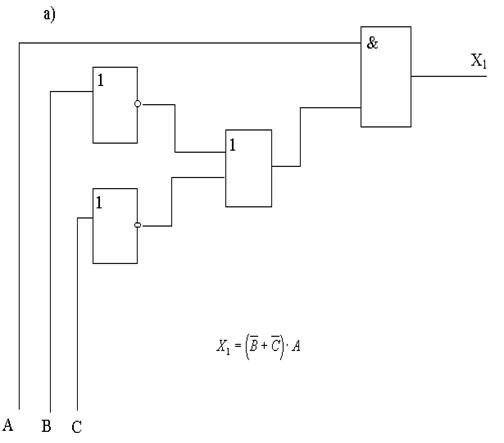
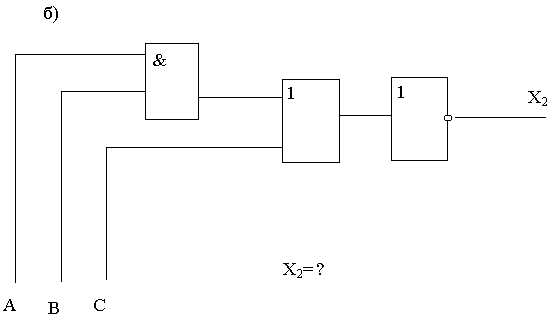

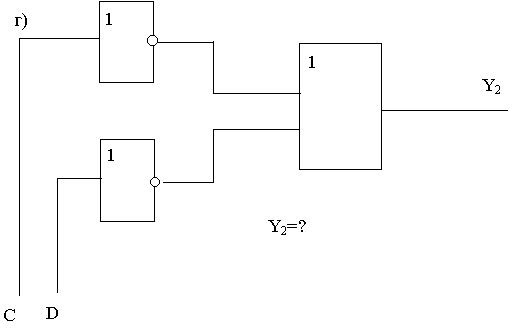

 .
.
 )
)


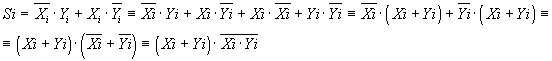
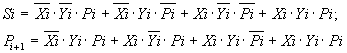



 ×
× 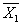 ×
×