Дифракция Фраунгофера на двух щелях.
Рассм. дифракцию на двух щелях, каждую из которых можно рассматривать как когерентные источники. Результирующая комплексная амплитуда будет определяться суммой амплитуд 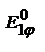 и
и 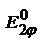 , создаваемых в направлении φ каждой щелью:
, создаваемых в направлении φ каждой щелью: 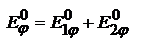 , где
, где 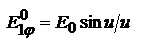 ,
, 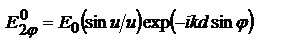 ,
, 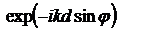 - сдвиг фаз между волнами, решив с-му:
- сдвиг фаз между волнами, решив с-му: 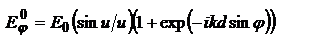 . интенсивность, создаваемую двумя щелями в направлении φ:
. интенсивность, создаваемую двумя щелями в направлении φ: 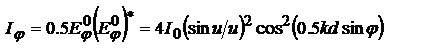 или
или  , т.е. интенсивность вследствие интерференции будет равна
, т.е. интенсивность вследствие интерференции будет равна 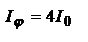 . Для углов
. Для углов 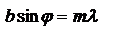 интенсивность равна 0 – главные минимумы,
интенсивность равна 0 – главные минимумы,  .
. 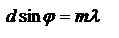 - главные максимумы
- главные максимумы  .
. 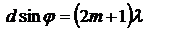 - дополнительные минимумы
- дополнительные минимумы 
Оптические свойства одноосных кристаллов. Обыкновенный и необыкновенный лучи.
 Опт. св-ва одноосных кристаллов описывается просто. К одноосным оптическим кристаллам относятся кристаллы, которые имеют тетрагональную, гексагональную и ромбоэдрическую кристаллические решётки. для кристаллов, имеющих кубическую решетку,
Опт. св-ва одноосных кристаллов описывается просто. К одноосным оптическим кристаллам относятся кристаллы, которые имеют тетрагональную, гексагональную и ромбоэдрическую кристаллические решётки. для кристаллов, имеющих кубическую решетку,  , т.е. они являются опт. изотропными. В случае одноосного кристалла векторы Е и В можно разложить на составляющие: вдоль оптической оси
, т.е. они являются опт. изотропными. В случае одноосного кристалла векторы Е и В можно разложить на составляющие: вдоль оптической оси 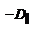 и
и 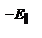 и составляющей перпендикулярно оптической оси
и составляющей перпендикулярно оптической оси 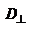 и
и 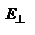 :
: 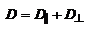 ,
,  , тогда
, тогда 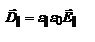 и
и 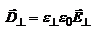 , где
, где  и
и 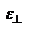 - продольная и поперечная диэлектрические проницаемости. Два случая: 1. Вектор D перпендикулярен гл. сечению кристалла. Тогда Е также перпендикулярен плоскости гл. сечения, и можно записать:
- продольная и поперечная диэлектрические проницаемости. Два случая: 1. Вектор D перпендикулярен гл. сечению кристалла. Тогда Е также перпендикулярен плоскости гл. сечения, и можно записать: 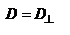 ,
, 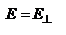 , тогда
, тогда 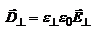 . Из ур-ий Максвелла:
. Из ур-ий Максвелла: 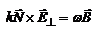 ,
, 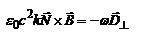 ,
,  , откуда
, откуда 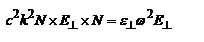 . Поскольку
. Поскольку 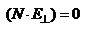 , то
, то 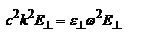
 . Обозначим фазовую скорость волны
. Обозначим фазовую скорость волны 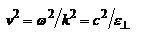 . Поскольку в нашем случае величины ω и k – вещественные и постоянные, то
. Поскольку в нашем случае величины ω и k – вещественные и постоянные, то 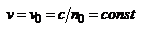 , где
, где 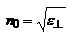 Полученный результат показывает, что скорость волны, поляризованной в плоскости, перпендикулярной плоскости падения (s-поляризация), не зависит от направления ее распространения. Такая волна называется обыкновенной. Величина n0 – показатель преломления света для обыкновенной волны - не зависит от направления ее распространения в кристалле. 2. Вектор D лежит в плоскости гл. сечения. В этом случае вектор Е тоже лежит в плоскости гл. сечения. Представим вектор Е в виде суммы
Полученный результат показывает, что скорость волны, поляризованной в плоскости, перпендикулярной плоскости падения (s-поляризация), не зависит от направления ее распространения. Такая волна называется обыкновенной. Величина n0 – показатель преломления света для обыкновенной волны - не зависит от направления ее распространения в кристалле. 2. Вектор D лежит в плоскости гл. сечения. В этом случае вектор Е тоже лежит в плоскости гл. сечения. Представим вектор Е в виде суммы 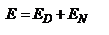 , где
, где 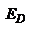 - составляющая вектора E вдоль D, EN – проекция на нормаль к оптической оси. Тогда можно записать
- составляющая вектора E вдоль D, EN – проекция на нормаль к оптической оси. Тогда можно записать 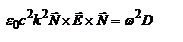 или
или  , после преобразований окончательно
, после преобразований окончательно  ,
, 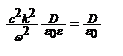 .Фазовая скорость
.Фазовая скорость 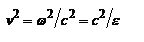 ,
, 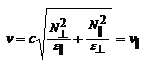 - показывает, что скорость
- показывает, что скорость 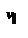 зависит от направления распространения волны. По этой причине волну, электрический вектор которой плоскости главного сечения, называют необыкновенной. Когда
зависит от направления распространения волны. По этой причине волну, электрический вектор которой плоскости главного сечения, называют необыкновенной. Когда 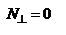 , то
, то  ,
, 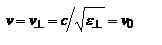 . Если необыкновенная волна распространяется вдоль опт. оси, ее скорость будет равна скорости распространения обыкновенной волны. Когда волна распространяется перпендикулярно опт. оси
. Если необыкновенная волна распространяется вдоль опт. оси, ее скорость будет равна скорости распространения обыкновенной волны. Когда волна распространяется перпендикулярно опт. оси 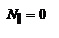 и
и 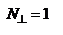 , скорость распространения:
, скорость распространения: 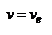 , где
, где 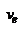 - скорость необыкновенной волны вдоль направления, перпендикулярного оптической оси кристалла. Можно также ввести соответствующие показатели преломления
- скорость необыкновенной волны вдоль направления, перпендикулярного оптической оси кристалла. Можно также ввести соответствующие показатели преломления 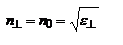 ,
, 
Энергия ЭМ волны, интенсивность.
При распространении электромагнитной волны происходит перенос энергии. объёмная плотн. энергии w представляет собой  сумму плотностей ЭМ энергии и энергии обусловленной ЭМ полем.
сумму плотностей ЭМ энергии и энергии обусловленной ЭМ полем. 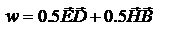 (*) - при лин. зависимости. Т.е.
(*) - при лин. зависимости. Т.е.  ,
, 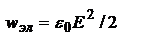 ,
, 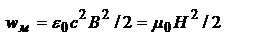 . Для ЭМ волны
. Для ЭМ волны 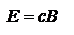 ,
, 
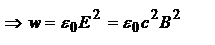 . Дифф. (*) по t, получаем ур-ие непрерывности для плотн. энергии ЭМ поля:
. Дифф. (*) по t, получаем ур-ие непрерывности для плотн. энергии ЭМ поля: 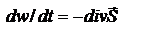 ,
, 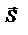 - в-р Пойтинга,
- в-р Пойтинга, 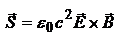 или
или  – плотность потока ЭМ энергии (мощность переносимая волной через ед. площадку, ориент.
– плотность потока ЭМ энергии (мощность переносимая волной через ед. площадку, ориент. 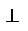 направлению распространения. Ур-ие непрерывности – з-н сохранения энергии для ЭМ поля, проинтегрируем его по объёму V, огр-му пов-тью
направлению распространения. Ур-ие непрерывности – з-н сохранения энергии для ЭМ поля, проинтегрируем его по объёму V, огр-му пов-тью  , юзаем т-му ОГ:
, юзаем т-му ОГ: 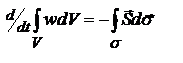 - интегр. форма Ур-ия непрерывности, показывает, что изм. энергии ЭМ поля в некотором объеме V, не содержащем зарядов и токов равно потоку энергии в этот объем через охватывающую его замкнутую пов-ть σ. направление вектора Пойнтинга совпадает с напр-ем вектора
- интегр. форма Ур-ия непрерывности, показывает, что изм. энергии ЭМ поля в некотором объеме V, не содержащем зарядов и токов равно потоку энергии в этот объем через охватывающую его замкнутую пов-ть σ. направление вектора Пойнтинга совпадает с напр-ем вектора  , т.е. энергия переносится в
, т.е. энергия переносится в 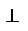 напр-нии к пов-м пост. фазы. Учитывая E
напр-нии к пов-м пост. фазы. Учитывая E 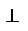 B, и
B, и 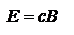 , получим:
, получим:  . S=cw – выражение - связь между объемной плотностью ЭМ энергии и плотн. ее потока. Поскольку
. S=cw – выражение - связь между объемной плотностью ЭМ энергии и плотн. ее потока. Поскольку 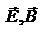 - функции времени и пространственных координат, то
- функции времени и пространственных координат, то 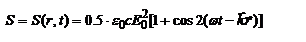 .
.
Физ. интерес - среднее по времени значение величины S - интенсивность I: 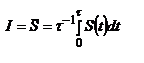 , где
, где 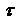 - промежуток времени
- промежуток времени 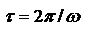 .
.  (#). Для изотропной среды, характеризуемой ε и μ:
(#). Для изотропной среды, характеризуемой ε и μ: 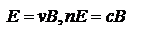
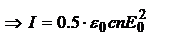 ,
,  - показатель преломления. Т.о.
- показатель преломления. Т.о. 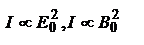 . Для монохроматических волн произведение E на комплексно сопряженную величину равно:
. Для монохроматических волн произведение E на комплексно сопряженную величину равно:  для величины, изменяющейся по гармоническому закону, операция ее умножения на комплексно сопряженную эквивалентна усреднению. ТО, если в выражении (#) под Е и Е0 понимать величины им пропорциональные
для величины, изменяющейся по гармоническому закону, операция ее умножения на комплексно сопряженную эквивалентна усреднению. ТО, если в выражении (#) под Е и Е0 понимать величины им пропорциональные 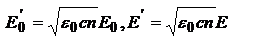 :
: 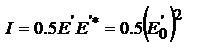 .
.
1.3. Суперпозиция ЭМ волн. Стоячие волны. Биения. Согласно принципу суперпозиции напряженность, создаваемая несколькими источниками стационарных электрических и магнитных полей, равна геометрической сумме полей, создаваемых каждым источником в отдельности E=E1+E2+…, B=B1+B2+…,. Принцип выполняется для слабых полей. В результате распространения пучка света большой интенсивности, среда может становиться анизотропной, и ее опт. свойства будут зависящими от его интенсивности. Полученная в результате сложения совокупность электрических и магнитных полей не обязательно является бегущей электромагнитной волной. Две плоские монохроматические волны с одинаковым волновым вектором  и одинаковой частоты
и одинаковой частоты  , которые распространяются в одном и том же направлении в результате сложения дают тоже плоскую монохроматическую волну той же частоты и того же направления.
, которые распространяются в одном и том же направлении в результате сложения дают тоже плоскую монохроматическую волну той же частоты и того же направления. 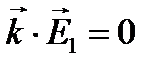 ,
, 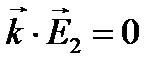 ,
, 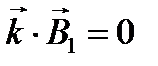
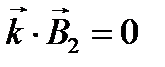 ,
, 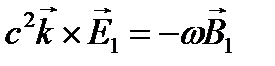 ,
, 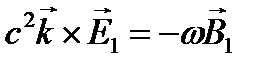 ,
, 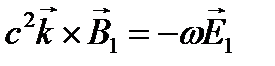 ,
,  ,
, 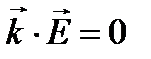 ,
,  ,
,  ,
, 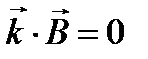 , где
, где 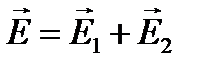 ,
, 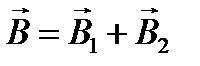 . Биения. Рассм. сложение волн с
. Биения. Рассм. сложение волн с  и
и  , распространяющихся в одном направлении. Возьмем случай, когда
, распространяющихся в одном направлении. Возьмем случай, когда 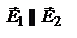 , это позволит заменить векторное сложение величин
, это позволит заменить векторное сложение величин  алгебраическим суммированием. Пусть
алгебраическим суммированием. Пусть  ,
, 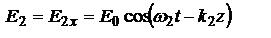 , суперпозиция:
, суперпозиция: 
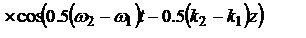 . Для опт. диапазона ЭМ волн хорошо выполняется
. Для опт. диапазона ЭМ волн хорошо выполняется 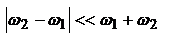 и
и 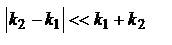 , обозначим
, обозначим 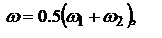

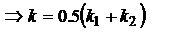 ,
,  тогда E:
тогда E: 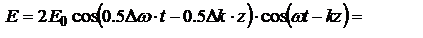
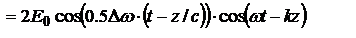 .Множитель
.Множитель 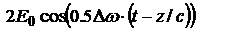 , можно Рассм. как амплитуду монохроматической волны с частотой
, можно Рассм. как амплитуду монохроматической волны с частотой 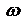 и волновым числом k. Данные колебания называют биениями, под которыми понимают гармонические колебания с плавно изменяющейся амплитудой. ТО, при сложении двух монохроматических волн разной частоты итоговая волна не будет монохроматической. Стоячие электромагнитные волны. Рассм. сложение двух электромагнитных волн одинаковой частоты и амплитуды, что распространяются навстречу друг другу. Например при отражении от идеального зеркала. Возьмем волны, в которых
и волновым числом k. Данные колебания называют биениями, под которыми понимают гармонические колебания с плавно изменяющейся амплитудой. ТО, при сложении двух монохроматических волн разной частоты итоговая волна не будет монохроматической. Стоячие электромагнитные волны. Рассм. сложение двух электромагнитных волн одинаковой частоты и амплитуды, что распространяются навстречу друг другу. Например при отражении от идеального зеркала. Возьмем волны, в которых  колеблется в плоскости XZ, а
колеблется в плоскости XZ, а  в YZ:
в YZ: 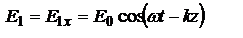 ,
, 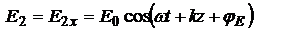 ,
, 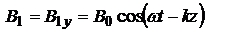 ,
, 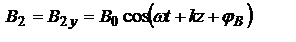 .
. 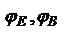 - сдвиг фаз при отражении. Учитывая E||B сложим:
- сдвиг фаз при отражении. Учитывая E||B сложим: 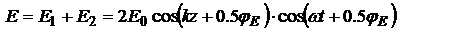 ,
, 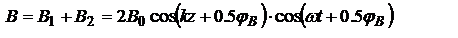 . Рассм. случай, когда показатель преломления среды, от которой отражается волна (n2), больше показателя преломления среды, где волна распространяется, т.е. n2>n1, в этом случае
. Рассм. случай, когда показатель преломления среды, от которой отражается волна (n2), больше показателя преломления среды, где волна распространяется, т.е. n2>n1, в этом случае 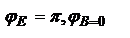
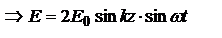 ,
, 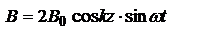
 волна не является бегущей т.к. фаза волны не содержит выражение
волна не является бегущей т.к. фаза волны не содержит выражение 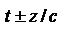 . Множитель
. Множитель 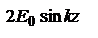 можно рассматривать как амплитуду волны в точке с координатой z. При изменении z напряженность во всех точках наложения волн изменяется с течением времени с одинаковой частотой и имеет в любой момент времени одинаковую фазу. Волна, все точки которой имеют одинаковую фазу, а амплитуда изменяется по гармоническому закону в зависимости от координаты z, называется стоячей. Точки с координатой n z, в которых наблюдается максимум для E или B называются пучностями. Точки, в которых величина Е или В имеют нулевые значение (для всех моментов времени t) называются узлами. Ко лебания E и B сдвинуты по фазе на четверть периода
можно рассматривать как амплитуду волны в точке с координатой z. При изменении z напряженность во всех точках наложения волн изменяется с течением времени с одинаковой частотой и имеет в любой момент времени одинаковую фазу. Волна, все точки которой имеют одинаковую фазу, а амплитуда изменяется по гармоническому закону в зависимости от координаты z, называется стоячей. Точки с координатой n z, в которых наблюдается максимум для E или B называются пучностями. Точки, в которых величина Е или В имеют нулевые значение (для всех моментов времени t) называются узлами. Ко лебания E и B сдвинуты по фазе на четверть периода  когда напряженность электрического поля достигает максимума, B=0. Плотность потока энергии ЭМ волн определяется вектором Пойнтинга. Так как в узлах величины E и B в любой момент времени равны нулю, то в этих точках поток равен нулю. Это означает, что через узлы и пучности отсутствует поток электромагнитной энергии, так как узлы для E совпадают с пучностями для B и наоборот. Однако, поскольку E и B в других точках изменяются с течением времени то можно заключить, что с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии электрического поля в энергию магнитного поля и наоборот. Суммарная энергия, которая заключена между двумя соседними узлами и пучностями, остается постоянной.
когда напряженность электрического поля достигает максимума, B=0. Плотность потока энергии ЭМ волн определяется вектором Пойнтинга. Так как в узлах величины E и B в любой момент времени равны нулю, то в этих точках поток равен нулю. Это означает, что через узлы и пучности отсутствует поток электромагнитной энергии, так как узлы для E совпадают с пучностями для B и наоборот. Однако, поскольку E и B в других точках изменяются с течением времени то можно заключить, что с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии электрического поля в энергию магнитного поля и наоборот. Суммарная энергия, которая заключена между двумя соседними узлами и пучностями, остается постоянной.
1.4. Поляризация ЭМ. свойства ЭМ волн зависят от направления колебаний векторов E и B, характеризуемого понятием поляризации. Если в процессе распространения волн вектор E (и B) изменяется только в одной плоскости, которая параллельна направлению их распространения, то такие волны называют линейно поляризованными. Плоскость колебаний вектора E называют плоскостью поляризации. Кроме линейной, бывают циркулярная или эллиптическая поляризации. Рассм. суперпозицию линейно поляризованных волн 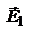 и
и  , имеющих одинаковую частоту w и распространяющихся в направлении оси Z, т.е.,
, имеющих одинаковую частоту w и распространяющихся в направлении оси Z, т.е., 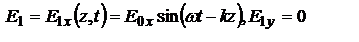 ,
,  . Суперпозиция:
. Суперпозиция: 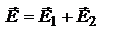 . С течением времени конец вектора E описывает в плоскости,
. С течением времени конец вектора E описывает в плоскости,  напр. движения волны, замкнутую кривую, найдём её:
напр. движения волны, замкнутую кривую, найдём её: 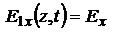 ,
,  . Запишем
. Запишем 
 ,
, 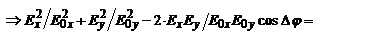
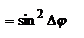 – ур-ие эллипса, главные оси которого образуют угол с осями Х и Y. Эллипс вписан в прямоугольник со сторонами, параллельными осям Х и Y. Аналогичная ситуация и для вектора B. Совершая движение по эллипсу, конец вектора E может вращаться по часовой (правая поляризация) или против часовой стрелки (левая). Возникающая поляризация, при которой конец вектора E описывает эллипс называется эллиптической. Направление вращения вектора E зависит от разности фаз
– ур-ие эллипса, главные оси которого образуют угол с осями Х и Y. Эллипс вписан в прямоугольник со сторонами, параллельными осям Х и Y. Аналогичная ситуация и для вектора B. Совершая движение по эллипсу, конец вектора E может вращаться по часовой (правая поляризация) или против часовой стрелки (левая). Возникающая поляризация, при которой конец вектора E описывает эллипс называется эллиптической. Направление вращения вектора E зависит от разности фаз 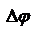 . Частные случаи:
. Частные случаи: 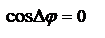
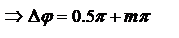 , тогда
, тогда 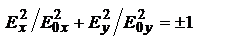 . Если
. Если 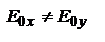 , то последнее ур-ие – ур-ие эллипса с центром в 0 и его полуоси
, то последнее ур-ие – ур-ие эллипса с центром в 0 и его полуоси 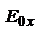 ,
, 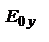 совпадут с Х и Y. При
совпадут с Х и Y. При 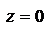
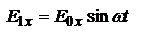 ,
, 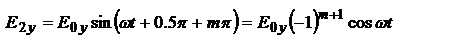 конец вектора E вращается с угловой скоростью
конец вектора E вращается с угловой скоростью 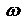 при четном m против часовой стрелки и при нечетном m — по часовой стрелке – это всё эллиптическая поляризация. Если
при четном m против часовой стрелки и при нечетном m — по часовой стрелке – это всё эллиптическая поляризация. Если  то – циркулярная. Если
то – циркулярная. Если  , тогда
, тогда 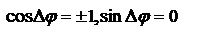 можно записать
можно записать 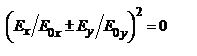 - описывает две прямые
- описывает две прямые 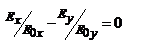 и
и 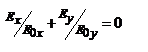 , причём
, причём  - результирующее линейное колебание будет возникать в 1 и 3 квадрате, а если
- результирующее линейное колебание будет возникать в 1 и 3 квадрате, а если 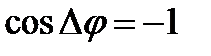 - во 2 и 4. Волна любой поляризации может быть получена в результате суперпозиции двух других, имеющих ортогональную поляризацию, т.е. для ЭМ волн
- во 2 и 4. Волна любой поляризации может быть получена в результате суперпозиции двух других, имеющих ортогональную поляризацию, т.е. для ЭМ волн  две независимые взаимно
две независимые взаимно 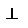 поляризации. Рассм. суперпозицию волн с левой и правой циркулярной поляризацией. Пусть при некотором z=0 векторы
поляризации. Рассм. суперпозицию волн с левой и правой циркулярной поляризацией. Пусть при некотором z=0 векторы  заданы ур-ми:
заданы ур-ми: 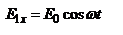 ,
,  ,
,  ,
, 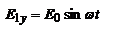 - 1 – с правой циркулярной поляризацией, 2 – с левой. Суперпозиция
- 1 – с правой циркулярной поляризацией, 2 – с левой. Суперпозиция 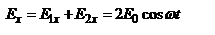 ,
, 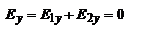 имеем волну с линейной поляризацией, причем линия колебаний совпадает с осью Х. Таким образом, любую линейно поляризованную волну можно представить как суперпозицию двух циркулярно поляризованных.
имеем волну с линейной поляризацией, причем линия колебаний совпадает с осью Х. Таким образом, любую линейно поляризованную волну можно представить как суперпозицию двух циркулярно поляризованных.
1.5 Фотометрия. Энергетические фотометрические величины. Основная - энергетический поток излучения 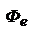 х-ет среднюю мощность излучения (<P>), которая переноситься ЭМ волной через пов-ть
х-ет среднюю мощность излучения (<P>), которая переноситься ЭМ волной через пов-ть  :
: 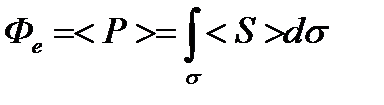 - по пов-ти. Энергетическая освещённость
- по пов-ти. Энергетическая освещённость  - если поток распределён неравномерно, то это средняя освещённость. Локальная формула:
- если поток распределён неравномерно, то это средняя освещённость. Локальная формула:  .
.  - энергетическая экспозиция (интегральный эффект, производимый ЭМ волной). Энергетической силой излучения - характеристика точечных источников
- энергетическая экспозиция (интегральный эффект, производимый ЭМ волной). Энергетической силой излучения - характеристика точечных источников 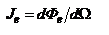 отношению величины потока излучения, излучаемого внутрь телесного угла dΩ, к величине этого угла. Мерой телесного угла является отношение площади
отношению величины потока излучения, излучаемого внутрь телесного угла dΩ, к величине этого угла. Мерой телесного угла является отношение площади  участка, вырезаемого на поверхности сферы конусом с вершиной в ее центре, к квадрату ее радиуса
участка, вырезаемого на поверхности сферы конусом с вершиной в ее центре, к квадрату ее радиуса  , телесный угол, опирающийся на произвольную площадку:
, телесный угол, опирающийся на произвольную площадку:  . Источники, у которых сила излучения одинакова по всем направлениям, называются изотропными. Для них:
. Источники, у которых сила излучения одинакова по всем направлениям, называются изотропными. Для них: 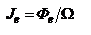 . Световой поток, излучаемый изотропным источником по всем направлениям:
. Световой поток, излучаемый изотропным источником по всем направлениям:  . Можно записать
. Можно записать 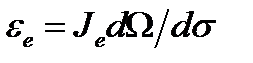 .ТО освещенность, создаваемая точечным источником, прямо пропорциональна косинусу угла между направлением падающих лучей и нормалью к освещаемой поверхности и обратно пропорциональна квадрату расстояния до источника. Энергетическая яркость - отношение потока, который излучается единичной видимой поверхности источника
.ТО освещенность, создаваемая точечным источником, прямо пропорциональна косинусу угла между направлением падающих лучей и нормалью к освещаемой поверхности и обратно пропорциональна квадрату расстояния до источника. Энергетическая яркость - отношение потока, который излучается единичной видимой поверхности источника  в телесный угол
в телесный угол 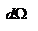 , к величине этого угла:
, к величине этого угла: 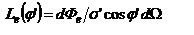 - сила света, создаваемая единичной видимой площадкой источника. Источники, яркость которых не зависит от направления излучения (
- сила света, создаваемая единичной видимой площадкой источника. Источники, яркость которых не зависит от направления излучения ( ) - ламбертовые. Для них з-н Ламберта:
) - ламбертовые. Для них з-н Ламберта: 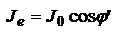 , где
, где 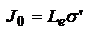 - сила излучения в нулевом направлении. Энергетическая светимость Ме - отношение полного энергетического потока, испускаемого протяженным источником по всем направлениям, к величине его площади:
- сила излучения в нулевом направлении. Энергетическая светимость Ме - отношение полного энергетического потока, испускаемого протяженным источником по всем направлениям, к величине его площади: 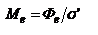 или
или 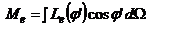 , для ламбертовых:
, для ламбертовых: 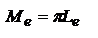 . Световые величины: сила света – кандела - сила света, испускаемого с поверхности площадью 1/60 см2 черного излучателя в перпендикулярном направлении при температуре затвердевания платины и давлении, равном 101 325 Па. Световой поток - сила света, испускаемая источником в телесный угол
. Световые величины: сила света – кандела - сила света, испускаемого с поверхности площадью 1/60 см2 черного излучателя в перпендикулярном направлении при температуре затвердевания платины и давлении, равном 101 325 Па. Световой поток - сила света, испускаемая источником в телесный угол  :
: 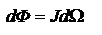 (люмен). Яркость – кд/м2, Освещённость – люкс. Спектральная световая эффективность - чувствительность «среднего» глаза человека для монохроматического излучения
(люмен). Яркость – кд/м2, Освещённость – люкс. Спектральная световая эффективность - чувствительность «среднего» глаза человека для монохроматического излучения 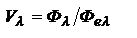 - отношение светового потока к энергетическому, создающему световой. Отношение спектральной световой эффективности
- отношение светового потока к энергетическому, создающему световой. Отношение спектральной световой эффективности
к максимальному значению  называется относительная спектральная эффективность
называется относительная спектральная эффективность  - зависимость
- зависимость 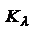 от
от 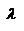 называется кривая видности. Если известна спектральная плотность энергетического потока излучения источника
называется кривая видности. Если известна спектральная плотность энергетического потока излучения источника 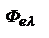 и
и 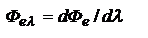 , то спектральную плотность соответствующего светового потока можно определить:
, то спектральную плотность соответствующего светового потока можно определить: 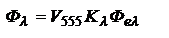 - связь энергетических и световых величин
- связь энергетических и световых величин
 1.6 Излучение ЭМ волн электрическим дипольным осциллятором. Излучение ЭМ волн опт. диапазона осуществляется атомами/молекулами. Простейшей моделью, позволяющей изучать возникновение ЭМ волн и их осн. х-ки, является диполь, образованный покоящимся зарядом –Q, расположенным в начале оси координат Z, и (+) зарядом Q, совершающим гармонические колебания. Дипольный момент с-мы будет также изменяться с течением времени по гармоническому закону:
1.6 Излучение ЭМ волн электрическим дипольным осциллятором. Излучение ЭМ волн опт. диапазона осуществляется атомами/молекулами. Простейшей моделью, позволяющей изучать возникновение ЭМ волн и их осн. х-ки, является диполь, образованный покоящимся зарядом –Q, расположенным в начале оси координат Z, и (+) зарядом Q, совершающим гармонические колебания. Дипольный момент с-мы будет также изменяться с течением времени по гармоническому закону: 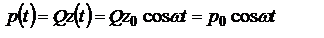 где z0 - амплитуда колебаний
где z0 - амплитуда колебаний  - max электрический момент диполя. Осцилляции дипольного момента могут совершаться как путем изменения расстояния между зарядами, так и путем изменения величины зарядов. Определим производные дипольного момента по времени
- max электрический момент диполя. Осцилляции дипольного момента могут совершаться как путем изменения расстояния между зарядами, так и путем изменения величины зарядов. Определим производные дипольного момента по времени  и
и 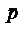 :
: 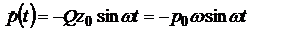 ,
, 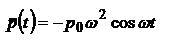 В классической электродинамике показывается, что величина индукции магн. поля и напр. электр. в волновой зоне будут равны соотв.
В классической электродинамике показывается, что величина индукции магн. поля и напр. электр. в волновой зоне будут равны соотв.  и
и 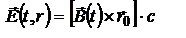 , где
, где 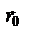 - ед. вектор, направленный из центра диполя в данную точку.
- ед. вектор, направленный из центра диполя в данную точку.  и
и 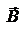 в момент времени t будут определяться расстоянием r от диполя до точки наблюдения и значением
в момент времени t будут определяться расстоянием r от диполя до точки наблюдения и значением 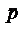 в момент времени t', причем
в момент времени t', причем 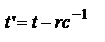 .
. 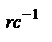 - в данной точке изменение электрического и магнитного полей наступит с опозданием, вызванным конечной скоростью распространения электромагнитных взаимодействий. Поскольку записанные выше соотношения для E, B содержат выражения
- в данной точке изменение электрического и магнитного полей наступит с опозданием, вызванным конечной скоростью распространения электромагнитных взаимодействий. Поскольку записанные выше соотношения для E, B содержат выражения  , то они представляют собой уравнения бегущих волн. Эти волны будут сферическими. ТО, эти ур-ия - бегущих сферических монохроматических волн, распр. со скоростью с. Эти волны - поперечные, поскольку E, B в соответствии со свойствами векторного уравнения изменяются в направлении
, то они представляют собой уравнения бегущих волн. Эти волны будут сферическими. ТО, эти ур-ия - бегущих сферических монохроматических волн, распр. со скоростью с. Эти волны - поперечные, поскольку E, B в соответствии со свойствами векторного уравнения изменяются в направлении  - направлению распространения волны. Для каждой точки волновой поверхности можно провести волновой вектор
- направлению распространения волны. Для каждой точки волновой поверхности можно провести волновой вектор  , направленный из начала координат. В волновой зоне волновая поверхность в окрестности некоторой точки может рассматриваться как участок плоскости. Для описания волн в таком случае можно использовать ур-ия плоских бегущих монохроматических волн.
, направленный из начала координат. В волновой зоне волновая поверхность в окрестности некоторой точки может рассматриваться как участок плоскости. Для описания волн в таком случае можно использовать ур-ия плоских бегущих монохроматических волн. 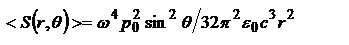 - интенсивность электромагнитной волны (доказывается сложно). Осциллирующий диполь излучает сферические волны. сферой в данном случае будет геом. место точек одинаковой фазой.
- интенсивность электромагнитной волны (доказывается сложно). Осциллирующий диполь излучает сферические волны. сферой в данном случае будет геом. место точек одинаковой фазой.
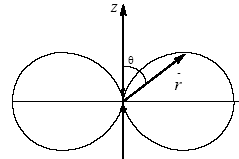 Угловая зависимость интенсивности, излучаемой диполем, определяемой квадратом амплитуды, задается множителем
Угловая зависимость интенсивности, излучаемой диполем, определяемой квадратом амплитуды, задается множителем 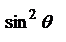 . Максимальная интенсивность излучается для
. Максимальная интенсивность излучается для 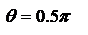 , т.е. в направлении, перпендикулярном оси диполя. В направлении осцилляции
, т.е. в направлении, перпендикулярном оси диполя. В направлении осцилляции 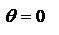 ) диполь не излучает. Угловая зависимость энергии, излучаемой диполем (диаграммой направленности). Обычно изображается в полярных координатах. В этом случае длина отрезка, проведенного из начала координат до пресечения с линией
) диполь не излучает. Угловая зависимость энергии, излучаемой диполем (диаграммой направленности). Обычно изображается в полярных координатах. В этом случае длина отрезка, проведенного из начала координат до пресечения с линией 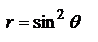 , пропорциональна интенсивности волны, распространяющейся в данном направлении.
, пропорциональна интенсивности волны, распространяющейся в данном направлении.
Затухание излучения классического осциллятора. Рассм. классический осциллятор – электрон, совершающий гармонические колебания с частотой  вдоль оси Z:
вдоль оси Z:  . Полная энергия колебаний:
. Полная энергия колебаний: 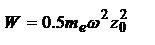 ,
, 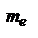 - масса. При свободном колебании осциллятора с частотой, благодаря излучению, ЭМ волна уносит с собой энергию. Изменение энергии в ед. времени = излучаемой им полной мощности:
- масса. При свободном колебании осциллятора с частотой, благодаря излучению, ЭМ волна уносит с собой энергию. Изменение энергии в ед. времени = излучаемой им полной мощности: 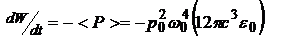 . С другой стороны, энергия, излучаемая осциллятором за время dt, будет равна
. С другой стороны, энергия, излучаемая осциллятором за время dt, будет равна  ,
, 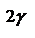 - коэфф. пропорциональности. Можно записать:
- коэфф. пропорциональности. Можно записать: 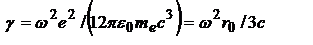 , где
, где 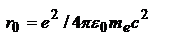 – классический радиус электрона. для определения свойств затухающего осциллятора используют величину
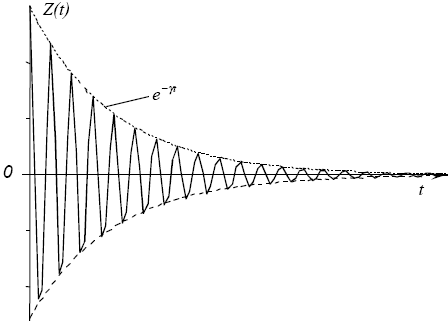
– классический радиус электрона. для определения свойств затухающего осциллятора используют величину 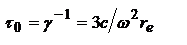 , которую называют временем радиационного (естественного) затухания классического осциллятора. вследствие излучения энергия осциллятора будет уменьшаться в соответствии с законом
, которую называют временем радиационного (естественного) затухания классического осциллятора. вследствие излучения энергия осциллятора будет уменьшаться в соответствии с законом 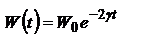 или
или 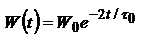 , где
, где 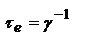 . Поскольку
. Поскольку 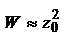 , то при излучении будет так же уменьшаться и амплитуда колебаний осциллятора в соответствии с законом
, то при излучении будет так же уменьшаться и амплитуда колебаний осциллятора в соответствии с законом  . Т.е. за время t =0 амплитуда колебаний уменьшится в e раз
. Т.е. за время t =0 амплитуда колебаний уменьшится в e раз
1.7 Спектральное разложение излучения. Монохроматические волны - идеализация. На самом деле всё не так. Все источники затухающие. Но немонохроматическую волну можно представить как совокупность монохроматических (спектральным разложение). Периодическая ф-ия 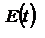 может быть представлена рядом Фурье
может быть представлена рядом Фурье 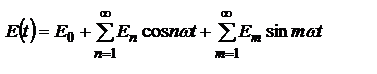 , где
, где 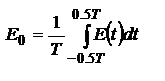 ,
, 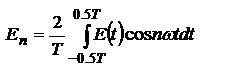 ,
, 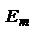 - тоже самое. В комплексной форме
- тоже самое. В комплексной форме  , где
, где 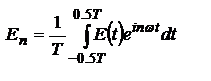 .
. 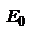 - постоянная составляющая поля, для ЭМ волн =0.
- постоянная составляющая поля, для ЭМ волн =0. 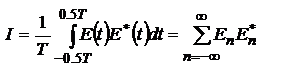 . Поскольку
. Поскольку 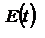 - вещественно, то
- вещественно, то 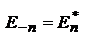
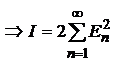 - т-ма Персеваля (средняя интенсивность волны равна сумме интенсивностей монохроматических компонент).
- т-ма Персеваля (средняя интенсивность волны равна сумме интенсивностей монохроматических компонент). 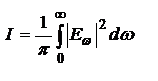 - т-ма Планшереля (интенсивность светового импульса определяется через интеграл по положительным частотам от ее спектральной плотности).
- т-ма Планшереля (интенсивность светового импульса определяется через интеграл по положительным частотам от ее спектральной плотности).  - спектральной плотностью интенсивности излучения.
- спектральной плотностью интенсивности излучения.
1.8 Спектральный состав квазимонохроматического света. 1. Рассм. спектральный состав немонохр. волны, предст. отрезок синусоиды 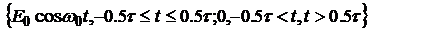 - с-ма.
- с-ма.  - пространственная длина цуга. Для опр. спектра юзаем интеграл Фурье
- пространственная длина цуга. Для опр. спектра юзаем интеграл Фурье 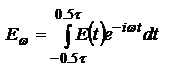 учитывая формулы Эйлера:
учитывая формулы Эйлера: 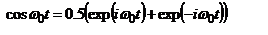 , приведём к виду
, приведём к виду 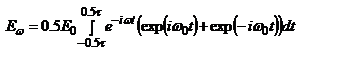 . Преобразовав
. Преобразовав 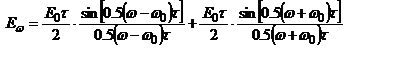 .
.
Вторым слагаемым можно пренебречь. При x=0 значение функции = 1– главный максимум. Функция обращается в нуль при 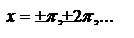 . В промежутках она имеет ряд дополнительных минимумов и максимумов. основные Фурье-компоненты отрезка синусоиды будут сосредоточены на интервале частот шириной
. В промежутках она имеет ряд дополнительных минимумов и максимумов. основные Фурье-компоненты отрезка синусоиды будут сосредоточены на интервале частот шириной 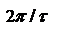 вблизи значений
вблизи значений  . Для характеристики спектрального распределения энергии достаточно рассмотреть функцию
. Для характеристики спектрального распределения энергии достаточно рассмотреть функцию 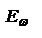 по (+)частотам
по (+)частотам 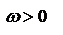 ,тогда
,тогда 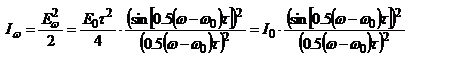 ,
, 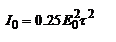 – max. зн. интенсивности при
– max. зн. интенсивности при 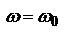 . Осн. энергия монохроматических направляющих сосредоточена в спектральном интервале
. Осн. энергия монохроматических направляющих сосредоточена в спектральном интервале 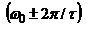 . В качестве спектральной ширины импульса часто принимают его ширину на половине высоты
. В качестве спектральной ширины импульса часто принимают его ширину на половине высоты 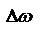 , т.е. интервал частот, при которых спектральная плотность равна половине max. Поскольку
, т.е. интервал частот, при которых спектральная плотность равна половине max. Поскольку 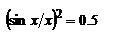 , при
, при  , то можно записать приближенное соотношение
, то можно записать приближенное соотношение 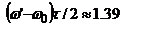 ,
,  - частота, при которой интенсивность
- частота, при которой интенсивность 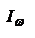 уменьшается в 2 раза.
уменьшается в 2 раза.  . Учитывая
. Учитывая 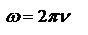 и
и 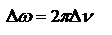 получим
получим 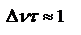 . Таким образом, чем большая продолжительность отрезка синусоиды, тем более узким будет ее спектральный диапазон, и тем более монохроматической будет волна. Волну, у которой
. Таким образом, чем большая продолжительность отрезка синусоиды, тем более узким будет ее спектральный диапазон, и тем более монохроматической будет волна. Волну, у которой  называют квазимонохр. Чем больше радиационное время затухания классического осциллятора, тем монохроматичнее будет излучение и тем уже будет его спектральная линия. Уширение спектра излучения классического осциллятора обусловлено конечной длиной цуга гармонических колебаний. Классический осциллятор, затухание которого вызвано только радиационными потерями вследствие излучения. Ширина спектральной линии
называют квазимонохр. Чем больше радиационное время затухания классического осциллятора, тем монохроматичнее будет излучение и тем уже будет его спектральная линия. Уширение спектра излучения классического осциллятора обусловлено конечной длиной цуга гармонических колебаний. Классический осциллятор, затухание которого вызвано только радиационными потерями вследствие излучения. Ширина спектральной линии  такого излучения называется естественной шириной. Естественная ширина спектральной линии определяется радиационным временем затухания.
такого излучения называется естественной шириной. Естественная ширина спектральной линии определяется радиационным временем затухания.


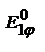 и
и 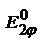 , создаваемых в направлении φ каждой щелью:
, создаваемых в направлении φ каждой щелью: 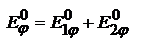 , где
, где 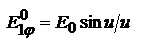 ,
, 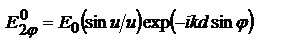 ,
, 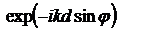 - сдвиг фаз между волнами, решив с-му:
- сдвиг фаз между волнами, решив с-му: 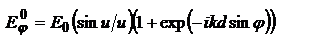 . интенсивность, создаваемую двумя щелями в направлении φ:
. интенсивность, создаваемую двумя щелями в направлении φ: 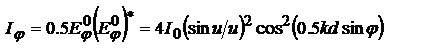 или
или  , т.е. интенсивность вследствие интерференции будет равна
, т.е. интенсивность вследствие интерференции будет равна 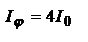 . Для углов
. Для углов 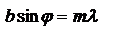 интенсивность равна 0 – главные минимумы,
интенсивность равна 0 – главные минимумы,  .
. 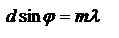 - главные максимумы
- главные максимумы  .
. 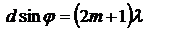 - дополнительные минимумы
- дополнительные минимумы  Опт. св-ва одноосных кристаллов описывается просто. К одноосным оптическим кристаллам относятся кристаллы, которые имеют тетрагональную, гексагональную и ромбоэдрическую кристаллические решётки. для кристаллов, имеющих кубическую решетку,
Опт. св-ва одноосных кристаллов описывается просто. К одноосным оптическим кристаллам относятся кристаллы, которые имеют тетрагональную, гексагональную и ромбоэдрическую кристаллические решётки. для кристаллов, имеющих кубическую решетку,  , т.е. они являются опт. изотропными. В случае одноосного кристалла векторы Е и В можно разложить на составляющие: вдоль оптической оси
, т.е. они являются опт. изотропными. В случае одноосного кристалла векторы Е и В можно разложить на составляющие: вдоль оптической оси 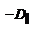 и
и 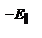 и составляющей перпендикулярно оптической оси
и составляющей перпендикулярно оптической оси 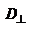 и
и 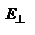 :
: 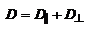 ,
,  , тогда
, тогда 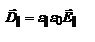 и
и 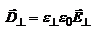 , где
, где  и
и 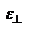 - продольная и поперечная диэлектрические проницаемости. Два случая: 1. Вектор D перпендикулярен гл. сечению кристалла. Тогда Е также перпендикулярен плоскости гл. сечения, и можно записать:
- продольная и поперечная диэлектрические проницаемости. Два случая: 1. Вектор D перпендикулярен гл. сечению кристалла. Тогда Е также перпендикулярен плоскости гл. сечения, и можно записать: 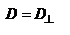 ,
, 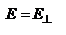 , тогда
, тогда 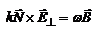 ,
, 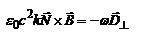 ,
,  , откуда
, откуда 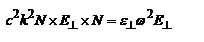 . Поскольку
. Поскольку 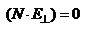 , то
, то 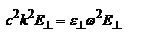
 . Обозначим фазовую скорость волны
. Обозначим фазовую скорость волны 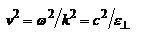 . Поскольку в нашем случае величины ω и k – вещественные и постоянные, то
. Поскольку в нашем случае величины ω и k – вещественные и постоянные, то 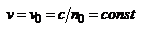 , где
, где 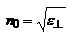 Полученный результат показывает, что скорость волны, поляризованной в плоскости, перпендикулярной плоскости падения (s-поляризация), не зависит от направления ее распространения. Такая волна называется обыкновенной. Величина n0 – показатель преломления света для обыкновенной волны - не зависит от направления ее распространения в кристалле. 2. Вектор D лежит в плоскости гл. сечения. В этом случае вектор Е тоже лежит в плоскости гл. сечения. Представим вектор Е в виде суммы
Полученный результат показывает, что скорость волны, поляризованной в плоскости, перпендикулярной плоскости падения (s-поляризация), не зависит от направления ее распространения. Такая волна называется обыкновенной. Величина n0 – показатель преломления света для обыкновенной волны - не зависит от направления ее распространения в кристалле. 2. Вектор D лежит в плоскости гл. сечения. В этом случае вектор Е тоже лежит в плоскости гл. сечения. Представим вектор Е в виде суммы 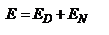 , где
, где 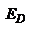 - составляющая вектора E вдоль D, EN – проекция на нормаль к оптической оси. Тогда можно записать
- составляющая вектора E вдоль D, EN – проекция на нормаль к оптической оси. Тогда можно записать 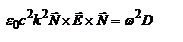 или
или  , после преобразований окончательно
, после преобразований окончательно  ,
, 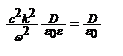 .Фазовая скорость
.Фазовая скорость 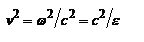 ,
, 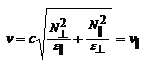 - показывает, что скорость
- показывает, что скорость 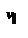 зависит от направления распространения волны. По этой причине волну, электрический вектор которой плоскости главного сечения, называют необыкновенной. Когда
зависит от направления распространения волны. По этой причине волну, электрический вектор которой плоскости главного сечения, называют необыкновенной. Когда 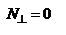 , то
, то  ,
, 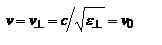 . Если необыкновенная волна распространяется вдоль опт. оси, ее скорость будет равна скорости распространения обыкновенной волны. Когда волна распространяется перпендикулярно опт. оси
. Если необыкновенная волна распространяется вдоль опт. оси, ее скорость будет равна скорости распространения обыкновенной волны. Когда волна распространяется перпендикулярно опт. оси 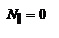 и
и 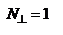 , скорость распространения:
, скорость распространения: 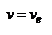 , где
, где 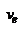 - скорость необыкновенной волны вдоль направления, перпендикулярного оптической оси кристалла. Можно также ввести соответствующие показатели преломления
- скорость необыкновенной волны вдоль направления, перпендикулярного оптической оси кристалла. Можно также ввести соответствующие показатели преломления 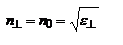 ,
, 
 сумму плотностей ЭМ энергии и энергии обусловленной ЭМ полем.
сумму плотностей ЭМ энергии и энергии обусловленной ЭМ полем. 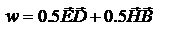 (*) - при лин. зависимости. Т.е.
(*) - при лин. зависимости. Т.е.  ,
, 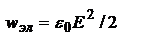 ,
, 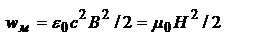 . Для ЭМ волны
. Для ЭМ волны 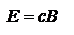 ,
, 
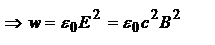 . Дифф. (*) по t, получаем ур-ие непрерывности для плотн. энергии ЭМ поля:
. Дифф. (*) по t, получаем ур-ие непрерывности для плотн. энергии ЭМ поля: 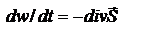 ,
, 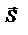 - в-р Пойтинга,
- в-р Пойтинга, 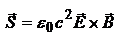 или
или  – плотность потока ЭМ энергии (мощность переносимая волной через ед. площадку, ориент.
– плотность потока ЭМ энергии (мощность переносимая волной через ед. площадку, ориент. 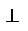 направлению распространения. Ур-ие непрерывности – з-н сохранения энергии для ЭМ поля, проинтегрируем его по объёму V, огр-му пов-тью
направлению распространения. Ур-ие непрерывности – з-н сохранения энергии для ЭМ поля, проинтегрируем его по объёму V, огр-му пов-тью  , юзаем т-му ОГ:
, юзаем т-му ОГ: 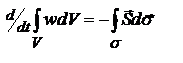 - интегр. форма Ур-ия непрерывности, показывает, что изм. энергии ЭМ поля в некотором объеме V, не содержащем зарядов и токов равно потоку энергии в этот объем через охватывающую его замкнутую пов-ть σ. направление вектора Пойнтинга совпадает с напр-ем вектора
- интегр. форма Ур-ия непрерывности, показывает, что изм. энергии ЭМ поля в некотором объеме V, не содержащем зарядов и токов равно потоку энергии в этот объем через охватывающую его замкнутую пов-ть σ. направление вектора Пойнтинга совпадает с напр-ем вектора  , т.е. энергия переносится в
, т.е. энергия переносится в 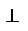 напр-нии к пов-м пост. фазы. Учитывая E
напр-нии к пов-м пост. фазы. Учитывая E 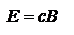 , получим:
, получим:  . S=cw – выражение - связь между объемной плотностью ЭМ энергии и плотн. ее потока. Поскольку
. S=cw – выражение - связь между объемной плотностью ЭМ энергии и плотн. ее потока. Поскольку 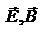 - функции времени и пространственных координат, то
- функции времени и пространственных координат, то 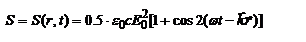 .
.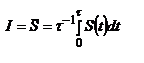 , где
, где 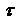 - промежуток времени
- промежуток времени 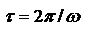 .
.  (#). Для изотропной среды, характеризуемой ε и μ:
(#). Для изотропной среды, характеризуемой ε и μ: 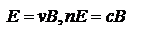
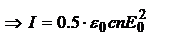 ,
,  - показатель преломления. Т.о.
- показатель преломления. Т.о. 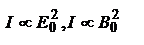 . Для монохроматических волн произведение E на комплексно сопряженную величину равно:
. Для монохроматических волн произведение E на комплексно сопряженную величину равно:  для величины, изменяющейся по гармоническому закону, операция ее умножения на комплексно сопряженную эквивалентна усреднению. ТО, если в выражении (#) под Е и Е0 понимать величины им пропорциональные
для величины, изменяющейся по гармоническому закону, операция ее умножения на комплексно сопряженную эквивалентна усреднению. ТО, если в выражении (#) под Е и Е0 понимать величины им пропорциональные 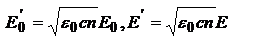 :
: 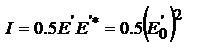 .
. и одинаковой частоты
и одинаковой частоты  , которые распространяются в одном и том же направлении в результате сложения дают тоже плоскую монохроматическую волну той же частоты и того же направления.
, которые распространяются в одном и том же направлении в результате сложения дают тоже плоскую монохроматическую волну той же частоты и того же направления. 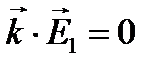 ,
, 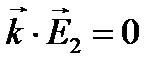 ,
, 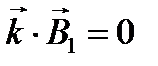
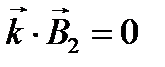 ,
, 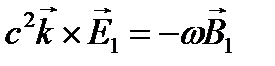 ,
, 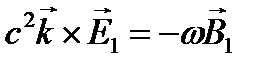 ,
, 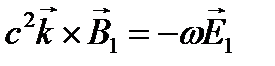 ,
,  ,
, 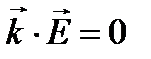 ,
,  ,
,  ,
, 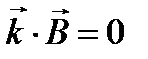 , где
, где 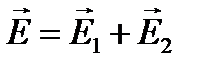 ,
, 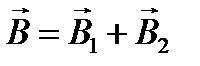 . Биения. Рассм. сложение волн с
. Биения. Рассм. сложение волн с  и
и  , распространяющихся в одном направлении. Возьмем случай, когда
, распространяющихся в одном направлении. Возьмем случай, когда 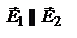 , это позволит заменить векторное сложение величин
, это позволит заменить векторное сложение величин  алгебраическим суммированием. Пусть
алгебраическим суммированием. Пусть  ,
, 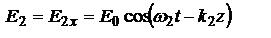 , суперпозиция:
, суперпозиция: 
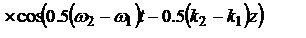 . Для опт. диапазона ЭМ волн хорошо выполняется
. Для опт. диапазона ЭМ волн хорошо выполняется 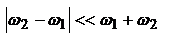 и
и 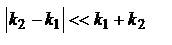 , обозначим
, обозначим 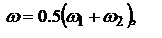

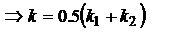 ,
,  тогда E:
тогда E: 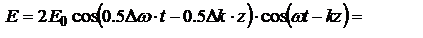
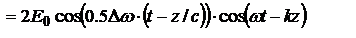 .Множитель
.Множитель 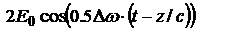 , можно Рассм. как амплитуду монохроматической волны с частотой
, можно Рассм. как амплитуду монохроматической волны с частотой  и волновым числом k. Данные колебания называют биениями, под которыми понимают гармонические колебания с плавно изменяющейся амплитудой. ТО, при сложении двух монохроматических волн разной частоты итоговая волна не будет монохроматической. Стоячие электромагнитные волны. Рассм. сложение двух электромагнитных волн одинаковой частоты и амплитуды, что распространяются навстречу друг другу. Например при отражении от идеального зеркала. Возьмем волны, в которых
и волновым числом k. Данные колебания называют биениями, под которыми понимают гармонические колебания с плавно изменяющейся амплитудой. ТО, при сложении двух монохроматических волн разной частоты итоговая волна не будет монохроматической. Стоячие электромагнитные волны. Рассм. сложение двух электромагнитных волн одинаковой частоты и амплитуды, что распространяются навстречу друг другу. Например при отражении от идеального зеркала. Возьмем волны, в которых  колеблется в плоскости XZ, а
колеблется в плоскости XZ, а  в YZ:
в YZ: 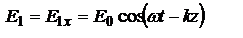 ,
, 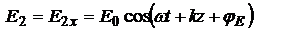 ,
, 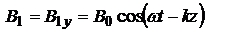 ,
, 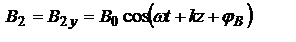 .
. 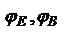 - сдвиг фаз при отражении. Учитывая E||B сложим:
- сдвиг фаз при отражении. Учитывая E||B сложим: 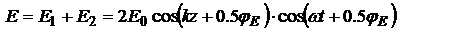 ,
, 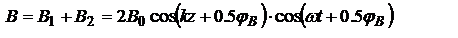 . Рассм. случай, когда показатель преломления среды, от которой отражается волна (n2), больше показателя преломления среды, где волна распространяется, т.е. n2>n1, в этом случае
. Рассм. случай, когда показатель преломления среды, от которой отражается волна (n2), больше показателя преломления среды, где волна распространяется, т.е. n2>n1, в этом случае 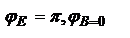
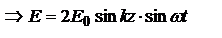 ,
, 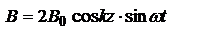
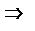 волна не является бегущей т.к. фаза волны не содержит выражение
волна не является бегущей т.к. фаза волны не содержит выражение 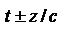 . Множитель
. Множитель 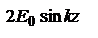 можно рассматривать как амплитуду волны в точке с координатой z. При изменении z напряженность во всех точках наложения волн изменяется с течением времени с одинаковой частотой и имеет в любой момент времени одинаковую фазу. Волна, все точки которой имеют одинаковую фазу, а амплитуда изменяется по гармоническому закону в зависимости от координаты z, называется стоячей. Точки с координатой n z, в которых наблюдается максимум для E или B называются пучностями. Точки, в которых величина Е или В имеют нулевые значение (для всех моментов времени t) называются узлами. Ко лебания E и B сдвинуты по фазе на четверть периода
можно рассматривать как амплитуду волны в точке с координатой z. При изменении z напряженность во всех точках наложения волн изменяется с течением времени с одинаковой частотой и имеет в любой момент времени одинаковую фазу. Волна, все точки которой имеют одинаковую фазу, а амплитуда изменяется по гармоническому закону в зависимости от координаты z, называется стоячей. Точки с координатой n z, в которых наблюдается максимум для E или B называются пучностями. Точки, в которых величина Е или В имеют нулевые значение (для всех моментов времени t) называются узлами. Ко лебания E и B сдвинуты по фазе на четверть периода  когда напряженность электрического поля достигает максимума, B=0. Плотность потока энергии ЭМ волн определяется вектором Пойнтинга. Так как в узлах величины E и B в любой момент времени равны нулю, то в этих точках поток равен нулю. Это означает, что через узлы и пучности отсутствует поток электромагнитной энергии, так как узлы для E совпадают с пучностями для B и наоборот. Однако, поскольку E и B в других точках изменяются с течением времени то можно заключить, что с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии электрического поля в энергию магнитного поля и наоборот. Суммарная энергия, которая заключена между двумя соседними узлами и пучностями, остается постоянной.
когда напряженность электрического поля достигает максимума, B=0. Плотность потока энергии ЭМ волн определяется вектором Пойнтинга. Так как в узлах величины E и B в любой момент времени равны нулю, то в этих точках поток равен нулю. Это означает, что через узлы и пучности отсутствует поток электромагнитной энергии, так как узлы для E совпадают с пучностями для B и наоборот. Однако, поскольку E и B в других точках изменяются с течением времени то можно заключить, что с течением времени энергия движется между соседними узлами и пучностями, превращаясь из энергии электрического поля в энергию магнитного поля и наоборот. Суммарная энергия, которая заключена между двумя соседними узлами и пучностями, остается постоянной.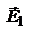 и
и  , имеющих одинаковую частоту w и распространяющихся в направлении оси Z, т.е.,
, имеющих одинаковую частоту w и распространяющихся в направлении оси Z, т.е., 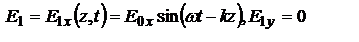 ,
,  . Суперпозиция:
. Суперпозиция: 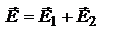 . С течением времени конец вектора E описывает в плоскости,
. С течением времени конец вектора E описывает в плоскости,  напр. движения волны, замкнутую кривую, найдём её:
напр. движения волны, замкнутую кривую, найдём её: 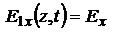 ,
,  . Запишем
. Запишем 
 ,
, 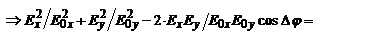
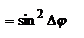 – ур-ие эллипса, главные оси которого образуют угол с осями Х и Y. Эллипс вписан в прямоугольник со сторонами, параллельными осям Х и Y. Аналогичная ситуация и для вектора B. Совершая движение по эллипсу, конец вектора E может вращаться по часовой (правая поляризация) или против часовой стрелки (левая). Возникающая поляризация, при которой конец вектора E описывает эллипс называется эллиптической. Направление вращения вектора E зависит от разности фаз
– ур-ие эллипса, главные оси которого образуют угол с осями Х и Y. Эллипс вписан в прямоугольник со сторонами, параллельными осям Х и Y. Аналогичная ситуация и для вектора B. Совершая движение по эллипсу, конец вектора E может вращаться по часовой (правая поляризация) или против часовой стрелки (левая). Возникающая поляризация, при которой конец вектора E описывает эллипс называется эллиптической. Направление вращения вектора E зависит от разности фаз 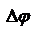 . Частные случаи:
. Частные случаи: 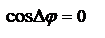
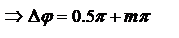 , тогда
, тогда 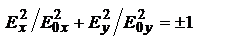 . Если
. Если 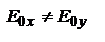 , то последнее ур-ие – ур-ие эллипса с центром в 0 и его полуоси
, то последнее ур-ие – ур-ие эллипса с центром в 0 и его полуоси 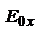 ,
, 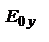 совпадут с Х и Y. При
совпадут с Х и Y. При 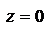
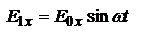 ,
, 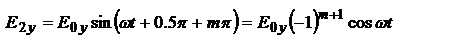 конец вектора E вращается с угловой скоростью
конец вектора E вращается с угловой скоростью 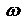 при четном m против часовой стрелки и при нечетном m — по часовой стрелке – это всё эллиптическая поляризация. Если
при четном m против часовой стрелки и при нечетном m — по часовой стрелке – это всё эллиптическая поляризация. Если  то – циркулярная. Если
то – циркулярная. Если  , тогда
, тогда 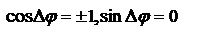 можно записать
можно записать 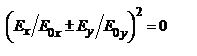 - описывает две прямые
- описывает две прямые 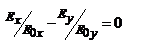 и
и 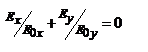 , причём
, причём  - результирующее линейное колебание будет возникать в 1 и 3 квадрате, а если
- результирующее линейное колебание будет возникать в 1 и 3 квадрате, а если 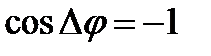 - во 2 и 4. Волна любой поляризации может быть получена в результате суперпозиции двух других, имеющих ортогональную поляризацию, т.е. для ЭМ волн
- во 2 и 4. Волна любой поляризации может быть получена в результате суперпозиции двух других, имеющих ортогональную поляризацию, т.е. для ЭМ волн  две независимые взаимно
две независимые взаимно 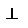 поляризации. Рассм. суперпозицию волн с левой и правой циркулярной поляризацией. Пусть при некотором z=0 векторы
поляризации. Рассм. суперпозицию волн с левой и правой циркулярной поляризацией. Пусть при некотором z=0 векторы  заданы ур-ми:
заданы ур-ми: 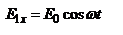 ,
,  ,
,  ,
, 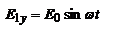 - 1 – с правой циркулярной поляризацией, 2 – с левой. Суперпозиция
- 1 – с правой циркулярной поляризацией, 2 – с левой. Суперпозиция 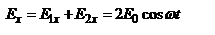 ,
, 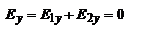 имеем волну с линейной поляризацией, причем линия колебаний совпадает с осью Х. Таким образом, любую линейно поляризованную волну можно представить как суперпозицию двух циркулярно поляризованных.
имеем волну с линейной поляризацией, причем линия колебаний совпадает с осью Х. Таким образом, любую линейно поляризованную волну можно представить как суперпозицию двух циркулярно поляризованных.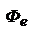 х-ет среднюю мощность излучения (<P>), которая переноситься ЭМ волной через пов-ть
х-ет среднюю мощность излучения (<P>), которая переноситься ЭМ волной через пов-ть  :
: 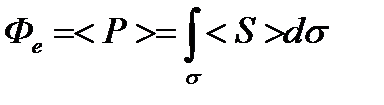 - по пов-ти. Энергетическая освещённость
- по пов-ти. Энергетическая освещённость  - если поток распределён неравномерно, то это средняя освещённость. Локальная формула:
- если поток распределён неравномерно, то это средняя освещённость. Локальная формула:  .
.  - энергетическая экспозиция (интегральный эффект, производимый ЭМ волной). Энергетической силой излучения - характеристика точечных источников
- энергетическая экспозиция (интегральный эффект, производимый ЭМ волной). Энергетической силой излучения - характеристика точечных источников 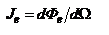 отношению величины потока излучения, излучаемого внутрь телесного угла dΩ, к величине этого угла. Мерой телесного угла является отношение площади
отношению величины потока излучения, излучаемого внутрь телесного угла dΩ, к величине этого угла. Мерой телесного угла является отношение площади  участка, вырезаемого на поверхности сферы конусом с вершиной в ее центре, к квадрату ее радиуса
участка, вырезаемого на поверхности сферы конусом с вершиной в ее центре, к квадрату ее радиуса  , телесный угол, опирающийся на произвольную площадку:
, телесный угол, опирающийся на произвольную площадку:  . Источники, у которых сила излучения одинакова по всем направлениям, называются изотропными. Для них:
. Источники, у которых сила излучения одинакова по всем направлениям, называются изотропными. Для них: 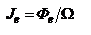 . Световой поток, излучаемый изотропным источником по всем направлениям:
. Световой поток, излучаемый изотропным источником по всем направлениям:  . Можно записать
. Можно записать 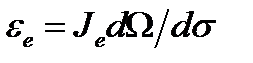 .ТО освещенность, создаваемая точечным источником, прямо пропорциональна косинусу угла между направлением падающих лучей и нормалью к освещаемой поверхности и обратно пропорциональна квадрату расстояния до источника. Энергетическая яркость - отношение потока, который излучается единичной видимой поверхности источника
.ТО освещенность, создаваемая точечным источником, прямо пропорциональна косинусу угла между направлением падающих лучей и нормалью к освещаемой поверхности и обратно пропорциональна квадрату расстояния до источника. Энергетическая яркость - отношение потока, который излучается единичной видимой поверхности источника  в телесный угол
в телесный угол 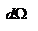 , к величине этого угла:
, к величине этого угла: 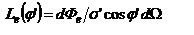 - сила света, создаваемая единичной видимой площадкой источника. Источники, яркость которых не зависит от направления излучения (
- сила света, создаваемая единичной видимой площадкой источника. Источники, яркость которых не зависит от направления излучения ( ) - ламбертовые. Для них з-н Ламберта:
) - ламбертовые. Для них з-н Ламберта: 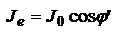 , где
, где 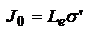 - сила излучения в нулевом направлении. Энергетическая светимость Ме - отношение полного энергетического потока, испускаемого протяженным источником по всем направлениям, к величине его площади:
- сила излучения в нулевом направлении. Энергетическая светимость Ме - отношение полного энергетического потока, испускаемого протяженным источником по всем направлениям, к величине его площади: 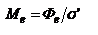 или
или 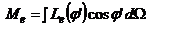 , для ламбертовых:
, для ламбертовых: 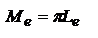 . Световые величины: сила света – кандела - сила света, испускаемого с поверхности площадью 1/60 см2 черного излучателя в перпендикулярном направлении при температуре затвердевания платины и давлении, равном 101 325 Па. Световой поток - сила света, испускаемая источником в телесный угол
. Световые величины: сила света – кандела - сила света, испускаемого с поверхности площадью 1/60 см2 черного излучателя в перпендикулярном направлении при температуре затвердевания платины и давлении, равном 101 325 Па. Световой поток - сила света, испускаемая источником в телесный угол  :
: 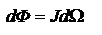 (люмен). Яркость – кд/м2, Освещённость – люкс. Спектральная световая эффективность - чувствительность «среднего» глаза человека для монохроматического излучения
(люмен). Яркость – кд/м2, Освещённость – люкс. Спектральная световая эффективность - чувствительность «среднего» глаза человека для монохроматического излучения 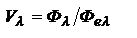 - отношение светового потока к энергетическому, создающему световой. Отношение спектральной световой эффективности
- отношение светового потока к энергетическому, создающему световой. Отношение спектральной световой эффективности называется относительная спектральная эффективность
называется относительная спектральная эффективность  - зависимость
- зависимость 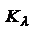 от
от 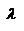 называется кривая видности. Если известна спектральная плотность энергетического потока излучения источника
называется кривая видности. Если известна спектральная плотность энергетического потока излучения источника 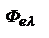 и
и 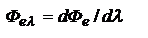 , то спектральную плотность соответствующего светового потока можно определить:
, то спектральную плотность соответствующего светового потока можно определить: 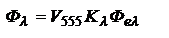 - связь энергетических и световых величин
- связь энергетических и световых величин 1.6 Излучение ЭМ волн электрическим дипольным осциллятором. Излучение ЭМ волн опт. диапазона осуществляется атомами/молекулами. Простейшей моделью, позволяющей изучать возникновение ЭМ волн и их осн. х-ки, является диполь, образованный покоящимся зарядом –Q, расположенным в начале оси координат Z, и (+) зарядом Q, совершающим гармонические колебания. Дипольный момент с-мы будет также изменяться с течением времени по гармоническому закону:
1.6 Излучение ЭМ волн электрическим дипольным осциллятором. Излучение ЭМ волн опт. диапазона осуществляется атомами/молекулами. Простейшей моделью, позволяющей изучать возникновение ЭМ волн и их осн. х-ки, является диполь, образованный покоящимся зарядом –Q, расположенным в начале оси координат Z, и (+) зарядом Q, совершающим гармонические колебания. Дипольный момент с-мы будет также изменяться с течением времени по гармоническому закону: 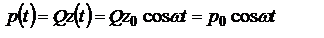 где z0 - амплитуда колебаний
где z0 - амплитуда колебаний  - max электрический момент диполя. Осцилляции дипольного момента могут совершаться как путем изменения расстояния между зарядами, так и путем изменения величины зарядов. Определим производные дипольного момента по времени
- max электрический момент диполя. Осцилляции дипольного момента могут совершаться как путем изменения расстояния между зарядами, так и путем изменения величины зарядов. Определим производные дипольного момента по времени  и
и 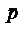 :
: 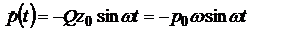 ,
, 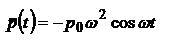 В классической электродинамике показывается, что величина индукции магн. поля и напр. электр. в волновой зоне будут равны соотв.
В классической электродинамике показывается, что величина индукции магн. поля и напр. электр. в волновой зоне будут равны соотв.  и
и 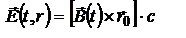 , где
, где 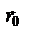 - ед. вектор, направленный из центра диполя в данную точку.
- ед. вектор, направленный из центра диполя в данную точку.  и
и 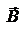 в момент времени t будут определяться расстоянием r от диполя до точки наблюдения и значением
в момент времени t будут определяться расстоянием r от диполя до точки наблюдения и значением 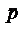 в момент времени t', причем
в момент времени t', причем 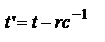 .
. 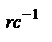 - в данной точке изменение электрического и магнитного полей наступит с опозданием, вызванным конечной скоростью распространения электромагнитных взаимодействий. Поскольку записанные выше соотношения для E, B содержат выражения
- в данной точке изменение электрического и магнитного полей наступит с опозданием, вызванным конечной скоростью распространения электромагнитных взаимодействий. Поскольку записанные выше соотношения для E, B содержат выражения  , то они представляют собой уравнения бегущих волн. Эти волны будут сферическими. ТО, эти ур-ия - бегущих сферических монохроматических волн, распр. со скоростью с. Эти волны - поперечные, поскольку E, B в соответствии со свойствами векторного уравнения изменяются в направлении
, то они представляют собой уравнения бегущих волн. Эти волны будут сферическими. ТО, эти ур-ия - бегущих сферических монохроматических волн, распр. со скоростью с. Эти волны - поперечные, поскольку E, B в соответствии со свойствами векторного уравнения изменяются в направлении  - направлению распространения волны. Для каждой точки волновой поверхности можно провести волновой вектор
- направлению распространения волны. Для каждой точки волновой поверхности можно провести волновой вектор  , направленный из начала координат. В волновой зоне волновая поверхность в окрестности некоторой точки может рассматриваться как участок плоскости. Для описания волн в таком случае можно использовать ур-ия плоских бегущих монохроматических волн.
, направленный из начала координат. В волновой зоне волновая поверхность в окрестности некоторой точки может рассматриваться как участок плоскости. Для описания волн в таком случае можно использовать ур-ия плоских бегущих монохроматических волн. 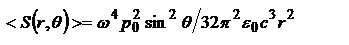 - интенсивность электромагнитной волны (доказывается сложно). Осциллирующий диполь излучает сферические волны. сферой в данном случае будет геом. место точек одинаковой фазой.
- интенсивность электромагнитной волны (доказывается сложно). Осциллирующий диполь излучает сферические волны. сферой в данном случае будет геом. место точек одинаковой фазой.
 Угловая зависимость интенсивности, излучаемой диполем, определяемой квадратом амплитуды, задается множителем
Угловая зависимость интенсивности, излучаемой диполем, определяемой квадратом амплитуды, задается множителем 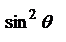 . Максимальная интенсивность излучается для
. Максимальная интенсивность излучается для 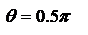 , т.е. в направлении, перпендикулярном оси диполя. В направлении осцилляции
, т.е. в направлении, перпендикулярном оси диполя. В направлении осцилляции 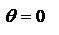 ) диполь не излучает. Угловая зависимость энергии, излучаемой диполем (диаграммой направленности). Обычно изображается в полярных координатах. В этом случае длина отрезка, проведенного из начала координат до пресечения с линией
) диполь не излучает. Угловая зависимость энергии, излучаемой диполем (диаграммой направленности). Обычно изображается в полярных координатах. В этом случае длина отрезка, проведенного из начала координат до пресечения с линией 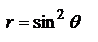 , пропорциональна интенсивности волны, распространяющейся в данном направлении.
, пропорциональна интенсивности волны, распространяющейся в данном направлении. вдоль оси Z:
вдоль оси Z:  . Полная энергия колебаний:
. Полная энергия колебаний: 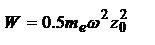 ,
, 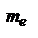 - масса. При свободном колебании осциллятора с частотой, благодаря излучению, ЭМ волна уносит с собой энергию. Изменение энергии в ед. времени = излучаемой им полной мощности:
- масса. При свободном колебании осциллятора с частотой, благодаря излучению, ЭМ волна уносит с собой энергию. Изменение энергии в ед. времени = излучаемой им полной мощности: 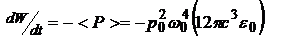 . С другой стороны, энергия, излучаемая осциллятором за время dt, будет равна
. С другой стороны, энергия, излучаемая осциллятором за время dt, будет равна  ,
, 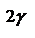 - коэфф. пропорциональности. Можно записать:
- коэфф. пропорциональности. Можно записать: 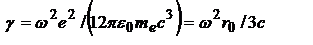 , где
, где 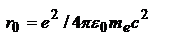 – классический радиус электрона. для определения свойств затухающего осциллятора используют величину
– классический радиус электрона. для определения свойств затухающего осциллятора используют величину 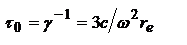 , которую называют временем радиационного (естественного) затухания классического осциллятора. вследствие излучения энергия осциллятора будет уменьшаться в соответствии с законом
, которую называют временем радиационного (естественного) затухания классического осциллятора. вследствие излучения энергия осциллятора будет уменьшаться в соответствии с законом 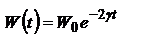 или
или 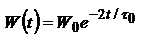 , где
, где 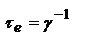 . Поскольку
. Поскольку 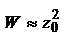 , то при излучении будет так же уменьшаться и амплитуда колебаний осциллятора в соответствии с законом
, то при излучении будет так же уменьшаться и амплитуда колебаний осциллятора в соответствии с законом  . Т.е. за время t =0 амплитуда колебаний уменьшится в e раз
. Т.е. за время t =0 амплитуда колебаний уменьшится в e раз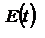 может быть представлена рядом Фурье
может быть представлена рядом Фурье 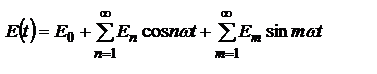 , где
, где 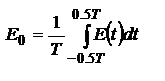 ,
, 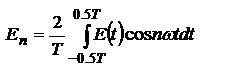 ,
, 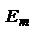 - тоже самое. В комплексной форме
- тоже самое. В комплексной форме  , где
, где 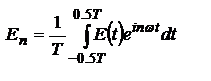 .
. 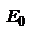 - постоянная составляющая поля, для ЭМ волн =0.
- постоянная составляющая поля, для ЭМ волн =0. 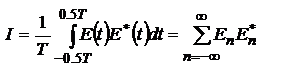 . Поскольку
. Поскольку 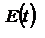 - вещественно, то
- вещественно, то 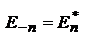
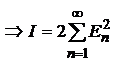 - т-ма Персеваля (средняя интенсивность волны равна сумме интенсивностей монохроматических компонент).
- т-ма Персеваля (средняя интенсивность волны равна сумме интенсивностей монохроматических компонент). 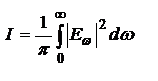 - т-ма Планшереля (интенсивность светового импульса определяется через интеграл по положительным частотам от ее спектральной плотности).
- т-ма Планшереля (интенсивность светового импульса определяется через интеграл по положительным частотам от ее спектральной плотности).  - спектральной плотностью интенсивности излучения.
- спектральной плотностью интенсивности излучения.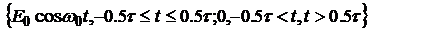 - с-ма.
- с-ма.  - пространственная длина цуга. Для опр. спектра юзаем интеграл Фурье
- пространственная длина цуга. Для опр. спектра юзаем интеграл Фурье 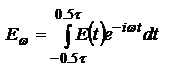 учитывая формулы Эйлера:
учитывая формулы Эйлера: 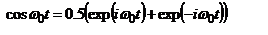 , приведём к виду
, приведём к виду 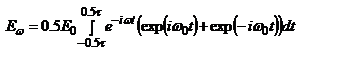 . Преобразовав
. Преобразовав 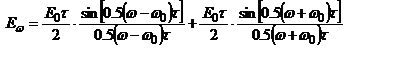 .
.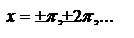 . В промежутках она имеет ряд дополнительных минимумов и максимумов. основные Фурье-компоненты отрезка синусоиды будут сосредоточены на интервале частот шириной
. В промежутках она имеет ряд дополнительных минимумов и максимумов. основные Фурье-компоненты отрезка синусоиды будут сосредоточены на интервале частот шириной 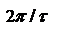 вблизи значений
вблизи значений  . Для характеристики спектрального распределения энергии достаточно рассмотреть функцию
. Для характеристики спектрального распределения энергии достаточно рассмотреть функцию 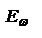 по (+)частотам
по (+)частотам 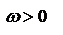 ,тогда
,тогда 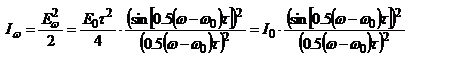 ,
, 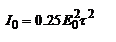 – max. зн. интенсивности при
– max. зн. интенсивности при 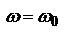 . Осн. энергия монохроматических направляющих сосредоточена в спектральном интервале
. Осн. энергия монохроматических направляющих сосредоточена в спектральном интервале 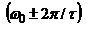 . В качестве спектральной ширины импульса часто принимают его ширину на половине высоты
. В качестве спектральной ширины импульса часто принимают его ширину на половине высоты 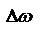 , т.е. интервал частот, при которых спектральная плотность равна половине max. Поскольку
, т.е. интервал частот, при которых спектральная плотность равна половине max. Поскольку 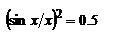 , при
, при  , то можно записать приближенное соотношение
, то можно записать приближенное соотношение 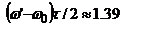 ,
,  - частота, при которой интенсивность
- частота, при которой интенсивность 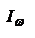 уменьшается в 2 раза.
уменьшается в 2 раза.  . Учитывая
. Учитывая 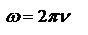 и
и 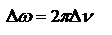 получим
получим 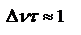 . Таким образом, чем большая продолжительность отрезка синусоиды, тем более узким будет ее спектральный диапазон, и тем более монохроматической будет волна. Волну, у которой
. Таким образом, чем большая продолжительность отрезка синусоиды, тем более узким будет ее спектральный диапазон, и тем более монохроматической будет волна. Волну, у которой  называют квазимонохр. Чем больше радиационное время затухания классического осциллятора, тем монохроматичнее будет излучение и тем уже будет его спектральная линия. Уширение спектра излучения классического осциллятора обусловлено конечной длиной цуга гармонических колебаний. Классический осциллятор, затухание которого вызвано только радиационными потерями вследствие излучения. Ширина спектральной линии
называют квазимонохр. Чем больше радиационное время затухания классического осциллятора, тем монохроматичнее будет излучение и тем уже будет его спектральная линия. Уширение спектра излучения классического осциллятора обусловлено конечной длиной цуга гармонических колебаний. Классический осциллятор, затухание которого вызвано только радиационными потерями вследствие излучения. Ширина спектральной линии  такого излучения называется естественной шириной. Естественная ширина спектральной линии определяется радиационным временем затухания.
такого излучения называется естественной шириной. Естественная ширина спектральной линии определяется радиационным временем затухания.


