Теорема про додавання пар сил

Теорема про додавання пар сил

Система пар сил, діючих на тверде тіло, еквівалентна одній парі

сил, векторний момент якої дорівнює геометричній сумі векторних моме-

нтів всіх пар системи.

 

5)

Головний вектор системи сил - вектор, який дорівнює геометричній сумі всіх сил системи:

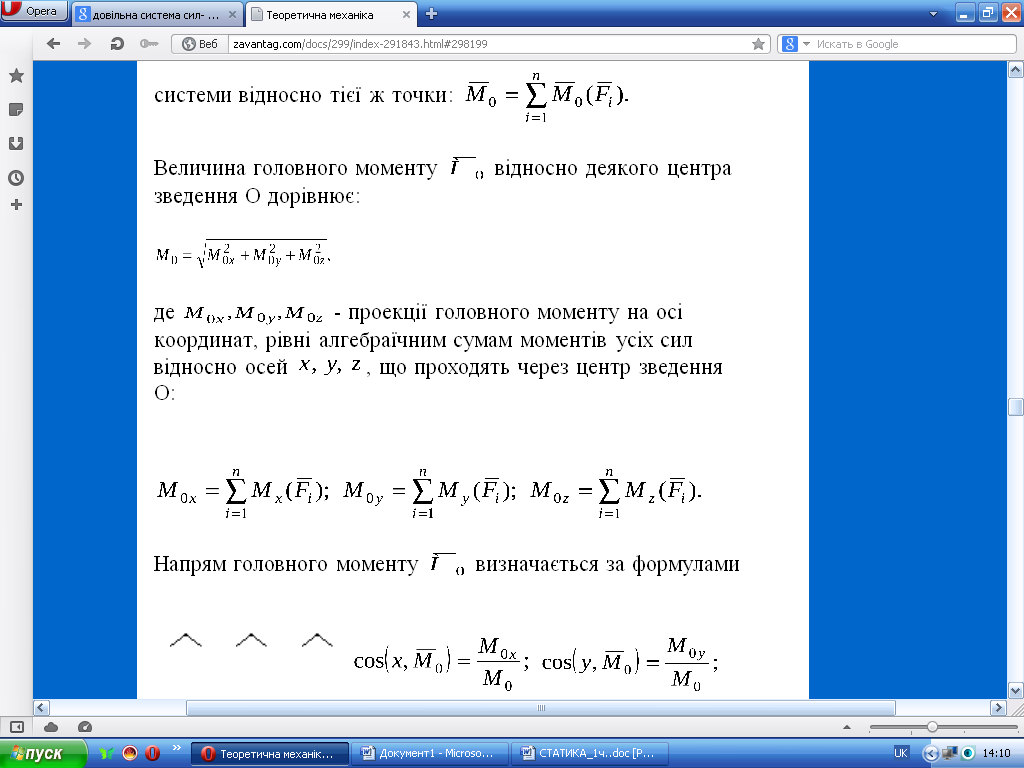
. Головний момент системи сил відносно точки О - вектор, який дорівнює геометричній сумі моментів сил системи відносно тієї ж точки:

Умови рівноваги довільної просторової системи сил: для рівноваги довільної просторової системи сил необхідно і достатньо, щоб головний вектор і головний момент цієї системи дорівнювали нулю (геометричні умови): F=0;M=0.

або суми проекцій усіх сил на кожну з трьох координатних осей і суми їх моментів відносно цих осей дорівнювали нулю (аналітичні умови):

6)

Теорема про паралельне перенесення сили

Силу можна переносити паралельно самій собі в будь-яку точку

твердого тіла, додаючи при цьому пару сил, векторний момент якої дорі-

внює векторному моменту сили, що переноситься, відносно нової точки її

прикладання.

7)

Закони тертя

 

Сила тертя завжди спрямована протилежно до напряму руху тіла.

 

Коефіцієнт тертя не залежить від площі контакту між тілами.

 

Коефіцієнт кінетичного тертя менше в порівнянні з коефіцієнтом статичного тертя.

 

Тертя не залежить від швидкості переміщення одного тіла по поверхні другого, але при великих швидкостях відмічається зменшення сили тертя.

Коефіціє́нт тертя́ — це величина, що характеризує силу тертя

Коефіціє́нт тертя́ ковзання — відношення сили тертя до реакції N, спрямованої по нормалі до поверхні дотику, яка виникає при прикладенні навантаження.

8)

центром ваги твердого

тіла називається незмінно зв’язана з цим тілом точка, через яку прохо-

дить лінія дії рівнодіючої сил ваги частинок цього тіла при будь-яких по-

ложенні тіла в просторі. [

9)

Кінематикою називається розділ механіки, в якому вивчається рух матеріальних тіл у просторі з геометричної точки зору, поза зв'язку з силами і масами, визначальним це рух.

Основне завдання кінематики полягає в тому, щоб знаючи закон руху даного тіла визначити всі кінематичні характеристики як самого тіла, так і його точок (траєкторію, швидкості, прискорення і т.д.).

Відносність - залежність механічного руху тіла від системи відліку. Не вказавши систему відліку, не має сенсу говорити про рух.

10)

Рух точки в просторі можна задати одним із трьох способів: вектор-

ним, координатним і натуральним.

Швидкістю точки - називається векторна величина, яка визначає швидкість зміни положення точки у просторі з часом.

 

Пришвидшенням точки - називається векторна величина, яка визначає швидкість зміни вектора швидкості точки з часом.

Швидкість та пришвидшення точки в полярних координатах

. Швидкість точки дорівнює векторній сумі радіальної і трансверсальної (поперечної) складових

Повне пришвидшення точки дорівнює векторній сумі радіального і трансверсального пришвидшень

11)

Задати рух точки векторним способом означає задати закон зміни радіуса-вектора точки з часом

При векторному способі задання руху точки (рис.2.8) прискорення виражається формулою

.

Кінематикою називається розділ механіки, в якому вивчається рух

матеріальних об’єктів (точок і тіл) без урахування їх інертності та діючих

на них сил.

Рух завжди розглядають відносно деякої системи відліку: зв’язаної з

деяким тілом (наприклад Землею) системи координат.

12)

Координатний спосіб. Положення точки відносно деякої системи

координат визначають координатами точки. У прямокутній декартовій си-

стемі координат цей спосіб полягає в вираженні координат x, y, z рухомої

точки (M) як відомих функцій часу:

13)

Натуральний спосіб. При натуральному способі задавання руху то-

чки повинна бути відома траєкторія точки із заданим на ній початком O і

додатнім напрямком відліку по дузі траєкторії дугової координати s точки

(рис. 67). Тоді положення точки M у будь який момент часу можна ви-

значити із залежності

s = s (t),

яку називають рівняння руху точки в натуральній формі

14)

20)

21) Механічною системою матеріальних точок або тіл називається така їх сукупність, в якій положення і рух кожної точки (тіла) залежить від положення і руху всіх інших.

22)Радіусом інерції тіла відносно даної осі називають відстань від осі до такої точки, в якій потрібно зосередити масу всього тіла

теоремою Гюйгенса:

момент інерції механічної системи (твердого тіла) відносно будь-якої осі дорівнює сумі момента інерції відносно осі, що проходить через центр мас цієї системи (тіла) паралельно даній, і добутку маси системи на квадрат відстані між цими осями.

23)

Сила інерції матеріальної точки за величиною дорівнює добутку маси точки на модуль її прискорення і має напрям, протилежний напряму прискорення (але не руху).

Таким чином, рівність (4.1) набуває вигляду:

.

(4.3)

Останнє рівняння і виражає принцип Даламбера:

для невільної матеріальної точки в кожний момент часу сума активних сил, що прикладені до точки, реакцій її в’язей і сили інерції дорівнює нулю.

главный вектор сил инерции системы материальных точек равен массе системы, умноженной на величину абсолютного ускорения центра масс, и направлен противоположно этому ускорению.

главный момент сил инерции системы относительно неподвижного центра O равен взятой со знаком минус производной по времени от момента количеств движения системы относительно того же центра.

24)

Теорема про додавання пар сил

Система пар сил, діючих на тверде тіло, еквівалентна одній парі

сил, векторний момент якої дорівнює геометричній сумі векторних моме-

нтів всіх пар системи.

 

5)

Головний вектор системи сил - вектор, який дорівнює геометричній сумі всіх сил системи:

. Головний момент системи сил відносно точки О - вектор, який дорівнює геометричній сумі моментів сил системи відносно тієї ж точки:

Умови рівноваги довільної просторової системи сил: для рівноваги довільної просторової системи сил необхідно і достатньо, щоб головний вектор і головний момент цієї системи дорівнювали нулю (геометричні умови): F=0;M=0.

або суми проекцій усіх сил на кожну з трьох координатних осей і суми їх моментів відносно цих осей дорівнювали нулю (аналітичні умови):

6)