
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменты инерции относительно параллельных осейСтр 1 из 3Следующая ⇒
Если извеcтны величины относительно осей z и y, тогда найдем Iz1 и Iy1 относительно осей z1 и y1. Используем общую формулу для осейвых моментов инерций: Iz1=∫y2dA=∫(y+a) 2dA=∫y2dA+2a∫ydA+a2∫dA =Iz+2aSz+a2A, y1=y+a Iy=∫z2dA=Iy+2bSy+ b2A Если Sz и Sy = 0,то формулы приобретают вид: Iz₁=Iz+a²A Iy₁=Iy+b²A – формулы параллельного переноса Момент инерции, относительно параллельных осей равен сумме момента инерции относит центр оси и произведения S(площади) фигуры на квадрат расстояния между этими осями.
Главные оси и главные моменты инерции Оси, относительно которых осевые моменты инерции имеют экстремальное значение, а центробежные моменты=0,называются главными осями инерции. Положение главных осей инерции определяется по формуле: tg2α=-2Dyz⁄Iz-Iy Положительный угол α откладывается от оси z против часовой стрелки, если главные оси проходят через центр тяжести сечения, то оси называются главными центральными осями. Осевыми моментами инерции относит главных центр осей,называются главными моментами инерции и вычисляются по формуле:
9. Основные гипотезы 1) Гипотеза сплошности: предполагает, что материал заполняет весь предоставленный ему объем 2) Гипотеза об однородности и изотропности: предполагает, что свойства материала одинаковы во всех точках и направлениях 3) Гипотеза об идеальной упругости: предполагает, что материал полностью восстанавливает свою форму после снятия нагрузки 4) Гипотеза о линейной зависимости между напряжениями и деформацией: предполагает, что напряжения прямо пропорциональны деформациям 5) Гипотеза о малости деформации: предполагает, что деформации (остаточные) малы по сравнению с размерами тела, и ими можно пренебречь
Понятие о напряжениях и деформациях Понятие о напряжениях и деформациях. Напряжение называется величина внутренней силы приходящейся на единицу поверхности. [Па], [Н/м2]. Рассмотрим элементарную площадку площадью ΔА, приложим в т.В элементарную силу ΔF и разложим ее на две составляющие ΔN и ΔQ. Полное напряжение в т.В определяется как предел Р= Проекции ΔF на ось У определяется как предел: Нормальные напряжения σ=
Допускаемые напряжения При проектировании конструкций необходимо поперечные размеры брать таким образом, чтобы они не превышали так называемых допускных. Различают: σ adm допускаемые нормальные напряжения τ adm – допускаемые касательные напряжения σ adm берется для хрупких материалов, как часть от предела прочности: σ adm = σl/n1 Для пластичных материалов на часть от предела текучести: σadm= Ϯadm = (0,5-0,6) Ϭadm
Напряжения и деформации при растяжении (сжатии). Закон Гука Растяжением(сжатием)называется такой вид деформации при котором возникает только один внутренний силовой фактор, продольная сила N. Δl=l₁ - l – абсолютная продольная деформация Δа=а₁-а, Δb = b₁-b – абсолютная поперечная деформация ξ= ξ′=Δа⁄а, ξ′=Δb/b – относительная поперечная деформация Отношение, относительно поперечной деформации к относит продольной деформации есть величина постоянная для каждого материала и называется коэффициентом пуассона | Установлена зависимость между напряжениеми и деформациями σ=Еξ – закон Гука, где Е – это модуль продолной упругости, [Мпа]. Модуль продольной упругости – споссобность материала сопротивляться продольным деформациям. Δl= Расчеты на прочность 1.Определение напряжения. Проверка прочности Ϭmax = N⁄A≤Ϭadm 2. Определение размера поперечного сечения А≥N⁄Ϭadm 3. Определение допускаемой нагрузки
N≤AϬadm
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.13.37 (0.006 с.) |
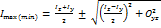
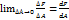 . Проекция ΔF на Х определяется как предел: касательной напряжения τ=
. Проекция ΔF на Х определяется как предел: касательной напряжения τ=  =
=  ; Q=∫τdA.
; Q=∫τdA. ; N=∫σdA. Нормальные напряжения действуют по нормали к поверхности, а в касательные напряжения по касательной. Различают линейные и угловые деформации. Линейными называют деформации, связанные с линейными изменениями тела (растяжение, сжатие). Угловые деформации связаны с изменением первоначально прямых углов (сдвиг, кручение).
; N=∫σdA. Нормальные напряжения действуют по нормали к поверхности, а в касательные напряжения по касательной. Различают линейные и угловые деформации. Линейными называют деформации, связанные с линейными изменениями тела (растяжение, сжатие). Угловые деформации связаны с изменением первоначально прямых углов (сдвиг, кручение). ; n₁ иn₂-коэффициент запаса прочности (и больше 1)
; n₁ иn₂-коэффициент запаса прочности (и больше 1) – относительная продольная деформация
– относительная продольная деформация |=υ (ню). Это величина безразмерная, 0÷0,5, коэф. Пуассона характеризует способность материала сопростивляться поперечной деформации.
|=υ (ню). Это величина безразмерная, 0÷0,5, коэф. Пуассона характеризует способность материала сопростивляться поперечной деформации. – закон Гука выраженный через удлинение, где А- это площадь поперечного сечения, а ЕА- жесткость при растяжении(сжатии).
– закон Гука выраженный через удлинение, где А- это площадь поперечного сечения, а ЕА- жесткость при растяжении(сжатии).


