
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моменты инерции простейших сечений.Стр 1 из 3Следующая ⇒
Расчетные схемы конструкции 1) Брус -тело, поперечные размеры которого намного меньше длины(балка-перекрытие) 2) Пластина -тело, один из р-ов которого намного меньше двух других(плита перекрытия, днище двутавра) 3) Оболочка -тело, ограниченное криволинейными поверхностями, расстояние между которыми намного меньше радиуса кривизны(купола зданий, стенки,стенки резервуаров) 4) Массив -тело, все размеры которого одного порядка(платины, опоры мостов)
Внешние, внутренние силы Внешними называются силы, которые действуют на тело со стороны других тел. Они подразделяются на сосредоточенные и распределенные.
Распределенные: q- равномерно-распределенная нагрузка (кН/м) Внутренними называются силы, возникающие внутри тела под действием внешних сил. Хаотично расположенные внутренние силы могут быть приведены к главному вектору и к главному моменту.
Метод сечения Рассмотрим брус с хаотично приложенными внешними силами F1, F2, F3, F4 1) В пределах бруса проводим сечение перпендикулярно оси стержня, которое делит наш брус на 2 части А и В 2) Отбросим одну из частей (часть А) 3) Действие отброшенной части заменим 6-ю внутренними силовыми факторами 4) Составим 6 уравнений равновесия a. ∑х = 0 → N b. ∑y = 0 → Qy c. ∑z = 0 →Qz d. ∑Mx = 0 → Mx e. ∑My = 0 → My f. ∑Mz = 0 → Mz Если какой либо из внутренних силовых факторов получится отрицательным, то следует поменять его направление на противоположное заданному.
Статические моменты сечений
ydA – момент элементарной площадки относительно Oz zdA – момент элементарной площадки относительно Оу
Статическими моментами относительно осей y и z называются интегралы: S - статический момент (см3) Sz = y∫dA ∫ydA Sy = z∫dA ∫zdA Статические моменты могут быть отрицательными, положительными и равными нулю. Статический момент сложной фигуры равен сумме статических моментов ее более простых составных частей.
Моменты инерции сечения Различают осевые, полярные и центробежные моменты инерции. Осевыми моментами инерции называется интеграл: Iz = ∫y2dA Iy = ∫z2dA (см4) Полярным интегралом инерции называется интеграл: Iƥ = ∫ƥ²dA
Центробежным моментом инерции называется интеграл: Dyz = ∫zydA Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Полярный и осевые моменты инерции могут быть только положительными.
Моменты инерции простейших сечений.
Iz = bh3/12 Iz = bh3/36 Iz = Iy = πd4/64 Iy = πd4/128 Iy = hb3/12 Iy = hb3/36 A = πd2/2 Iy=hb³⁄36Iz=πd⁴⁄128 Iz1= 0.11r4
Моменты инерции относительно параллельных осей Если Sz и Sy = 0,то формулы приобретают вид: Iz₁=Iz+a²A Iy₁=Iy+b²A – формулы параллельного переноса Момент инерции, относительно параллельных осей равен сумме момента инерции относит центр оси и произведения S(площади) фигуры на квадрат расстояния между этими осями.
Главные оси и главные моменты инерции Оси, относительно которых осевые моменты инерции имеют экстремальное значение, а центробежные моменты=0,называются главными осями инерции. Положение главных осей инерции определяется по формуле: tg₂α=-2Dyz⁄Iz-Iy Положительный угол α откладывается от оси z против часовой стрелки, если главные оси проходят через центр тяжести сечения, то оси называются главными центральными осями. Осевыми моментами инерции относит главных центр осей,называются главными моментами инерции и вычисляются по формуле:
9. Основные гипотезы 1) Гипотеза сплошности: предполагает, что материал заполняет весь предоставленный ему объем 2) Гипотеза об однородности и изотропности: предполагает, что свойства материала одинаковы во всех точках и направлениях 3) Гипотеза об идеальной упругости: предполагает, что материал полностью восстанавливает свою форму после снятия нагрузки 4) Гипотеза о линейной зависимости между напряжениями и деформацией: предполагает, что напряжения прямо пропорциональны деформациям 5) Гипотеза о малости деформации: предполагает, что деформации (остаточные) малы по сравнению с размерами тела, и ими можно пренебречь
Допускаемые напряжения При проектировании конструкций необходимо поперечные размеры брать таким образом, чтобы они не превышали так называемых допускных. Различают:
σ adm допускаемые нормальные напряжения τ adm – допускаемые касательные напряжения σ adm берется для хрупких материалов, как часть от предела прочности: σ adm = σl/n1 Для пластичных материалов на часть от предела текучести: Ϭadm-Ϯт⁄n₂ n₁ иn₂-коэффициент запаса прочности (и больше 1) Ϯadm = (0,5-0,6) Ϭadm
Расчеты на прочность 1.Определение напряжения. Проверка прочности Ϭmax = N⁄A≤Ϭadm 2. Определение размера поперечного сечения А≥N⁄Ϭadm 3. Определение допускаемой нагрузки N≤AϬadm
Метод начальных параметров Недостатком метода непосредственного интегрирования является необходимость определения большого количества произвольных постоянных. Если балка имеет n-участков, то необходимо составить и решить систему 2n алгебраических уравнений. В методе начальных параметров независимо от количества участков, следует определить 2 произвольные постоянные.
Е – модуль упругости Iz – момент инерции относительно Оz υ – прогиб в рассматриваемой точке начальные параметры: υ0 – начальный прогиб θо – начальный угол поворота х – расстояние от начала балки до рассматриваемого сечения
Постоянные интегрирования имеют здесь простой смысл: это начальные (при x = 0) значения искомой функции и ее производные. Поэтому, метод интегрирования дифференциальных уравнений, основанный на формуле, и широко применяемый в строительной механике, называется методом начальных параметров. Согласно метода начальных параметров, балка разбивается на участки. Подставив (12.38) в (12.39), получим функцию прогибов на I участке балки:
Метод конечных разностей Прогибы простейших балок
С жесткой заделкой: Слева – заделка; справа – сила, направленная вниз; прогиб – плавно переходит с 0 в заделке к силе.
Слева – заделка; на всем протяжении – равномерно-распределенная нагрузка; прогиб как с силой – плавный переход вниз.
Рациональные сечения балок Рациональным называется сечение, имеющее наибольшую прочность и экономичность. При изгибе наибольшие нормальные напряжения возникают в местах наиболее удаленных от оси z. Чем ближе к Оz, тем нормальные напряжения меньше, а на самой оси они равны нулю Так и с материалом: его наибольшее количество должно быть сосредоточено намного меньше. Таким образом было получено двутавровое поперечное сечение, в котором служат для восприятия нормальных напряжений, а стенка служит для соединения полок и восприятия касательных напряжений, возникающих под действием поперечных сил.
Балка равного сопротивления БРС называется балка поперечного сечения, у которой максимальные напряжения во всех сечениях одинаковы и равны допускаемым
Форма БРС определяется из формулы:
Сдвиг (срез). Основные понятия Сдвиг (срез) – вид напряженно-деформированного состояния, при котором в поперечном сечении возникает только один внутренний силовой фактор. На сдвиг(срез) рассчитывают сварные болтовые соединения и т.д. При сдвиге в сечении возникают касательные напряжения
Опасные точки сечения Опасными являются точки, наиболее удаленные от нейтральной линии
Для их определения следует через все крайние точки сечения провести линии параллельные нейтральной Наиболее удаленные от НЛ будут проходить через опасные точки сечения
Расчетные схемы конструкции 1) Брус -тело, поперечные размеры которого намного меньше длины(балка-перекрытие) 2) Пластина -тело, один из р-ов которого намного меньше двух других(плита перекрытия, днище двутавра) 3) Оболочка -тело, ограниченное криволинейными поверхностями, расстояние между которыми намного меньше радиуса кривизны(купола зданий, стенки,стенки резервуаров) 4) Массив -тело, все размеры которого одного порядка(платины, опоры мостов)
Внешние, внутренние силы Внешними называются силы, которые действуют на тело со стороны других тел. Они подразделяются на сосредоточенные и распределенные.
Распределенные: q- равномерно-распределенная нагрузка (кН/м) Внутренними называются силы, возникающие внутри тела под действием внешних сил. Хаотично расположенные внутренние силы могут быть приведены к главному вектору и к главному моменту.
Метод сечения Рассмотрим брус с хаотично приложенными внешними силами F1, F2, F3, F4 1) В пределах бруса проводим сечение перпендикулярно оси стержня, которое делит наш брус на 2 части А и В 2) Отбросим одну из частей (часть А) 3) Действие отброшенной части заменим 6-ю внутренними силовыми факторами 4) Составим 6 уравнений равновесия a. ∑х = 0 → N b. ∑y = 0 → Qy c. ∑z = 0 →Qz d. ∑Mx = 0 → Mx e. ∑My = 0 → My f. ∑Mz = 0 → Mz Если какой либо из внутренних силовых факторов получится отрицательным, то следует поменять его направление на противоположное заданному.
Статические моменты сечений
ydA – момент элементарной площадки относительно Oz zdA – момент элементарной площадки относительно Оу
Статическими моментами относительно осей y и z называются интегралы: S - статический момент (см3) Sz = y∫dA ∫ydA Sy = z∫dA ∫zdA Статические моменты могут быть отрицательными, положительными и равными нулю. Статический момент сложной фигуры равен сумме статических моментов ее более простых составных частей.
Моменты инерции сечения Различают осевые, полярные и центробежные моменты инерции. Осевыми моментами инерции называется интеграл: Iz = ∫y2dA
Iy = ∫z2dA (см4) Полярным интегралом инерции называется интеграл: Iƥ = ∫ƥ²dA Центробежным моментом инерции называется интеграл: Dyz = ∫zydA Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Полярный и осевые моменты инерции могут быть только положительными.
Моменты инерции простейших сечений.
Iz = bh3/12 Iz = bh3/36 Iz = Iy = πd4/64 Iy = πd4/128 Iy = hb3/12 Iy = hb3/36 A = πd2/2 Iy=hb³⁄36Iz=πd⁴⁄128 Iz1= 0.11r4
|
||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 898; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.187 (0.046 с.) |
 Сосредоточенные:
Сосредоточенные: F- сосредоточенная сила (кН)
F- сосредоточенная сила (кН) Ме- пара сил, момент (кН*м)
Ме- пара сил, момент (кН*м)





















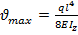


 Q – поперечная сила; А – площадь поперечного сечения
Q – поперечная сила; А – площадь поперечного сечения


