Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Косой удар тела о неподвижную поверхность.
Скорость тела до удара v направлена под углом падения α к общей нормали n тела и поверхности (рис. 1,б). После удара тело отскакивает от неподвижной поверхности со скоростью u под углом отражения β к общей нормали h. Между скоростями u и v и между углами α и β имеет место соотношение:
где λ - коэффициент мгновенного трения, определяемый экспериментально (часто полагают λ=0). рис. 1 α – угол падения β – угол отражения Прямой центральный удар двух тел- Частные случаи. Скорости тел v1 и v2 до удара направлены по их общей нормали, проходящей через их центры масс. Различают две фазы удара: первая фаза: от момента соприкосновения тел до момента, когда все точки соударяющихся тел приобретут общую скорость u и оба тела получат максимальную деформацию. Скорость u в конце фазы:
где m1 - масса первого тела; m2 - масса второго тела; вторая фаза: с момента окончания первой фазы до того момента, когда тела под действием упругих сил частично восстановят свою форму, приобретут разные скорости u1 и u2 и разъединятся. Скорости тел после удара:
Полный ударный импульс, полученный каждым из тел при ударе:
где знак минус берется для первого тела, а знак плюс для второго. Потеря кинетической энергии при ударе. Теорема Карно. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, ПОТЕРЯННАЯ ПРИ УДАРЕ. При ударе часть кинетической энергии ударяющихся тел?T теряется, т. е. переходит в немеханические формы:
где Т* - кинетическая энергия потерянных скоростей v1-u1 и v2-u2:
Частные случаи: k=0,
k=1,?T=0 (потери энергии не происходит). Удар по вращающемуся телу. Удар по вращающемуся телу. При исследовании удара по вращающемуся телу кроме теоремы об изменении количества движения приходится использовать и закон моментов. Относительно оси вращения его запишем так Правую часть надо немного преобразовать. Найдем, сначала, интеграл момента ударной силы относительно неподвижной точки О:
При этом предполагалось, что за малое время удара τ радиус-вектор Проектируя результат этого векторного равенства на ось вращения z, проходящую через точку О, получим
В качестве примера рассмотрим удар вращающегося тела о неподвижную преграду. Тело, вращаясь вокруг горизонтальной оси О, ударяется о преграду А (рис.114). Определим ударные импульсы сил, возникающих в подшипниках на оси,
По теореме об изменении количества движения
где скорости центра масс С в начале и конце удара Третье уравнение, по (10), получится в виде И, так как коэффициент восстановления
то Находим импульсы реакции оси:
Обязательно надо обратить внимание на то, что при Место, точка удара, расположенная на этом расстоянии Кстати, заметим, что центр удара совпадает с точкой где приложены равнодействующая сил инерции и вектор количества движения. Вспомним, что при ударе длинной палкой по неподвижному предмету, мы нередко испытывали рукой неприятный ударный импульс, как говорят – «отбивали руку». Нетрудно найти в этом случае центр удара – место, которым следует ударить, чтобы не почувствовать это неприятное ощущение (рис.115).
Рис.115
Так как
Следовательно, центр удара находится на расстоянии трети длины от конца палки. Понятие центра удара учитывают при создании различных ударных механизмов и других конструкций, где встречаются ударные процессы.
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 615; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.209.95 (0.035 с.) |








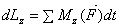 и, после интегрирования за время удара
и, после интегрирования за время удара  ,
,  или
или  где
где  и
и  - угловые скорости тела в начале и в конце удара,
- угловые скорости тела в начале и в конце удара,  - ударные силы.
- ударные силы.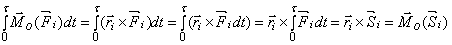 .
. считался неизменным, постоянным.
считался неизменным, постоянным. , т.е. интеграл равен моменту вектора импульса ударной силы относительно оси вращения. Закон моментов в преобразованном виде запишется, теперь, так:
, т.е. интеграл равен моменту вектора импульса ударной силы относительно оси вращения. Закон моментов в преобразованном виде запишется, теперь, так: . (10)
. (10)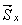 и
и 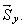
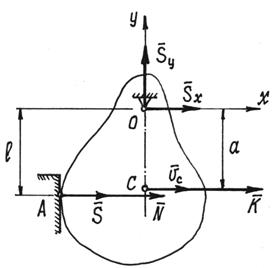 Рис.114
Рис.114 в проекциях на оси х и у получим два уравнения:
в проекциях на оси х и у получим два уравнения:

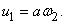 Поэтому первое уравнение станет таким
Поэтому первое уравнение станет таким 
 из которого находим
из которого находим 

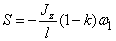 (в нашем примере
(в нашем примере  поэтому ударный импульс S > 0, то есть направлен так, как показано на рисунке).
поэтому ударный импульс S > 0, то есть направлен так, как показано на рисунке).

 ударные импульсы в подшипниках оси будут равны нулю.
ударные импульсы в подшипниках оси будут равны нулю. от оси вращения, называется центром удара. При ударе по телу в этом месте ударные силы в подшипниках не возникают.
от оси вращения, называется центром удара. При ударе по телу в этом месте ударные силы в подшипниках не возникают.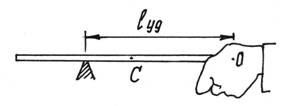
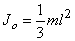 (l – длина палки) и
(l – длина палки) и  то
то