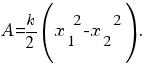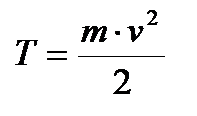Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения движения материальной точки в декартовых прямоугольных координатах и в проекциях на естественные оси.Стр 1 из 2Следующая ⇒
Предмет динамики. Основные понятия. Законы классической механики. Динамика- раздел теоретической механики, изучающий движение материальных объектов с учетом сил, вызывающих это движение. Две основные задачи динамики: 1.по заданному движению точки определить силы, вызывающие это движение. 2. по заданным силам определить движение точки. В динамике рассматриваются различные модели материальных объектов. Простейшая модель - материальная точка (тело, формами и размерами которого можно пренебречь в условиях данной задачи). Более сложные материальные объекты — система материальных точек и твердое тело. Основные законы классической механики Ньютона. 1687 издал работу Математические начала натурфилософии – основа классической механики Излагает 3 закона: 1)Тело сохраняет состояние покоя пока на него не оказ. Воздействие др. тела (закон инеркции) Инерктность- способность тела сопротивлятся воздействию на него сил 2)Ускорение кот приобретает тело в рез-те воздействия на него прямо пропорционально вызывающей его силе и обратно пропорц. Массе тела Q=F/m Сла-физич мера вз-я тел или матер.точек 3) объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой F12, а второе — на первое с силой F21. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
Дифференциальные уравнения движения материальной точки в декартовых прямоугольных координатах и в проекциях на естественные оси. Дифференциальные уравнения движения материальной точки в декартовых координатах. m*d^2x/dt^2=ΣFkx, m*d^2y/dt^2=ΣFky, m*d^2z/dt^2=ΣFkz Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трёхгранника. Проекция на Mτnb: m*dv/dt=ΣFkτ, m*dv/dt=ΣFkn, m*dv/dt=ΣFkb
Две основные задачи динамики материальной точки (МТ). В динамике точки решаются две основные задачи. Первая (прямая) задача динамики. По заданному движению, совершаемому точкой данной массы, требуется найти неизвестную действующую силу.
Вторая (обратная) задача динамики. По заданным силам, действующим на точку данной массы, и заданным начальным условиям движения требуется найти закон движения точки. Это — основные (классические) задачи динамики точки, сформулированные самим основоположником динамики И. Ньютоном. С последующим развитием динамики появились новые задачи, сочетающие в себе черты обеих названных задач. Например, при несвободном движении точки реакции связей заранее неизвестны, и вторая задача приобретает смешанный характер — требуется найти как закон движения точки, так и реакции связей. Появились задачи об оптимальном движении, о движении точки с переменной массой и много других задач, тесно связанных с потребностями развивающейся техники. Основным математическим инструментом для решения задач динамики точки служат основное уравнение динамики и вытекающие из него дифференциальные уравнения движения.
Механическая система (МС). Классификация сил, действующих на МС: силы внешние и внутренние, задаваемые (активные) и реакции связей. Свойства внутренних сил. Моменты инерции системы и твердого тела относительно плоскости, оси и полюса. Радиус инерции. 1)Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до оси.
где: mi — масса i-й точки, ri — расстояние от i-й точки до оси. 2)Моментом инерции твёрдого тела относительно плоскости называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояний от этой точки до плоскости. 3)Моментом инерции твёрдого тела относительно полюса (полярным моментом инерции) называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от точки до этого полюса. Радиус инерции, величина r, имеющая размерность длины, с помощью которой момент инерции тела относительно данной оси выражается формулой I = Мr2, где М - масса тела. Главные оси инерции Кроме указанного выше единственного случая, осевые моменты инерции в нуль не обращаются и всегда положительны. Что же касается центробежных моментов инерции, то они могут быть положительными, отрицательными и принимать нулевые значения. Если два центробежных момента инерции, содержащие в обозначениях общий индекс некоторой оси, равны нулю, то эта ось называется главной осью инерции тела (в точке пересечения осей). Например, если имеем Jxz = Jyz = 0, то ось z является главной осью инерции в точке О (начале координат). Если равны нулю все три центробежных момента инерции, то все три оси являются главными.
Существует теорема, которая устанавливает, что в каждой точке тела можно найти как минимум три главные оси инерции. Главные оси, построенные в центре масс тела, называются главными центральными осями инерции, а моменты инерции относительно этих осей — главными центральными моментами инерции. Тензор инерции — в механике абсолютно твёрдого тела — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью:
Где J — тензор инерции,w— угловая скорость,L— момент импульса Осевой момент инерции Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
где: § mi — масса i -й точки, § ri — расстояние от i -й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где: § dm = ρ dV — масса малого элемента объёма тела dV, § ρ — плотность, § r — расстояние от элемента dV до оси a. Если тело однородно, то есть его плотность всюду одинакова, то
Эллипсо́ид ине́рции — геометрическая фигура в виде поверхности второго порядка, которая характеризует тензор инерции твёрдого тела относительно его центра масс. Физический маятник. Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела. Работа силы. Мерой действия силы при превращении механического движения в другую форму движения является работа силы. Работа постоянной по модулю и направлению силы F на прямолинейном перемещении s ее точки приложения равна
Если угол α острый, то работа силы положительна, если тупой – отрицательна. Если направления силы и перемещения совпадают (α=0), то A = Fs; Если направление силы перпендикулярно направлению перемещения (α=90◦), то А = 0; Если направление силы противоположно направлению перемещения (α=180◦), то A = -Fs. Элементарная работа силы F на перемещении точки из одного положения в другое по криволинейной траектории δA = Fδs cos (F,v), где δs – пройденный точкой элементарный путь; ∠F, v – угол, составленный направлением силы F и скоростью v. В случае переменной силы определяется элементарная работа на малом перемещении, и после суммирования элементарных работ получается
Мощность Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Различают среднюю мощность за промежуток времени
и мгновенную мощность в данный момент времени:
Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:
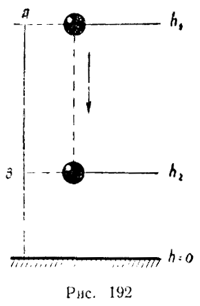
Работа силы тяжести Сила тяжести равна F = mg и направлена по вертикали вниз. Вблизи поверхности Земли ее можно считать постоянной. При движении тела по вертикали вниз сила тяжести совпадает по направлению с перемещением. При переходе с высоты h1 над каким-то уровнем, от которого мы начинаем отсчет высоты, до высоты h2 над тем же уровнем (рис. 192), тело совершает перемещение, по абсолютной величине равное h1 - h2.
Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:
Высоты h1 и h2 не обязательно отсчитывать от поверхности Земли. Для начала отсчета высот можно выбрать любой уровень. Это может быть пол комнаты, стол или стул, это может быть и дно ямы, вырытой в земле, и т. д. Ведь в формулу для работы входит разность высот, а она не зависит от того, откуда начинать их отсчет. Мы могли бы, например, условиться начинать отсчет высоты с уровня В (см. рис. 192). Тогда высота этого уровня была бы равна нулю, а работа выражалась бы равенством A=m*g*h где h — высота точки A над уровнем В.
Работа силы упругости Сила упругости, как мы знаем, возникает при деформации тел. По своему абсолютному значению она пропорциональна величине деформации (удлинению), а направлена в сторону, противоположную направлению смещения точек тела при деформации. На рисунке 199, а показана пружина в ее естественном, недеформированном состоянии. Правый конец пружины закреплен, а к левому прикреплено тело. Если пружину сжать, сместив левый ее конец па расстояние x1 (рис. 199, б), то возникнет сила упругости, действующая со стороны пружины на тело, равная: F1упр=—kx1 где k — жесткость пружины.
Предположим, что левый конец пружины переместился из положения А в положение В (рис. 199, в). В этом положении деформация пружины равна уже не х1, а х2. Значит, конец пружины переместился на расстояние х2 — х1. Чтобы вычислить работу, нужно это перемещение умножить на силу. Но сила упругости в отличие от силы тяжести вблизи поверхности Земли при движении тела изменяется от точки к точке. Если в начальной точке она была равна —kx1, то в конечной точке (в точке В) она стала равной —kx2.
Для того чтобы вычислить работу силы упругости, нужно взять среднее значение силы упругости и умножить его на перемещение х2 — х1. Сила упругости пропорциональна деформации пружины. Поэтому среднее значение силы упругости можно найти, используя метод, который был использован при нахождении среднего значения скорости при равноускоренном движении. На это-то значение силы упругости и нужно умножить перемещение х2 — х1 чтобы получить работу этой силы:
Кинетическая энергия точки Кинетической энергией материальной точки (или ее живой силой) называют половину произведения массы точки на квадрат ее скорости.
Предмет динамики. Основные понятия. Законы классической механики. Динамика- раздел теоретической механики, изучающий движение материальных объектов с учетом сил, вызывающих это движение. Две основные задачи динамики: 1.по заданному движению точки определить силы, вызывающие это движение. 2. по заданным силам определить движение точки. В динамике рассматриваются различные модели материальных объектов. Простейшая модель - материальная точка (тело, формами и размерами которого можно пренебречь в условиях данной задачи). Более сложные материальные объекты — система материальных точек и твердое тело. Основные законы классической механики Ньютона. 1687 издал работу Математические начала натурфилософии – основа классической механики Излагает 3 закона: 1)Тело сохраняет состояние покоя пока на него не оказ. Воздействие др. тела (закон инеркции) Инерктность- способность тела сопротивлятся воздействию на него сил 2)Ускорение кот приобретает тело в рез-те воздействия на него прямо пропорционально вызывающей его силе и обратно пропорц. Массе тела Q=F/m Сла-физич мера вз-я тел или матер.точек 3) объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой F12, а второе — на первое с силой F21. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
Дифференциальные уравнения движения материальной точки в декартовых прямоугольных координатах и в проекциях на естественные оси. Дифференциальные уравнения движения материальной точки в декартовых координатах. m*d^2x/dt^2=ΣFkx, m*d^2y/dt^2=ΣFky, m*d^2z/dt^2=ΣFkz Дифференциальные уравнения движения материальной точки в проекциях на оси естественного трёхгранника. Проекция на Mτnb: m*dv/dt=ΣFkτ, m*dv/dt=ΣFkn, m*dv/dt=ΣFkb
|
||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.247.196 (0.051 с.) |


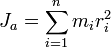 ,
, ,
,
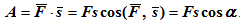
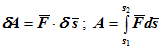
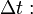
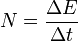

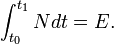


 Так как
Так как 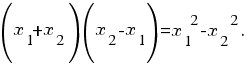 то формула для работы принимает вид:
то формула для работы принимает вид: