
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение движения центра масс
где Далее следует, что если
1.4 Динамика вращательного движения твердого тела Вращательным движением твердого тела вокруг неподвижнойосиназывается такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.13). Проходящая через неподвижные точки А и В прямая АВ называется осью вращения.при вращательном движении все точки, принадлежащие оси вращения, будут неподвижны, а все остальные точки тела будут описывать окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла Уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси. Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость Если за промежуток времени
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения СИ: кг·м². Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где:
Если тело однородно, то есть его плотность всюду одинакова, то
основное уравнение динамики вращательного движения твердого тела вокруг неподвижной оси. Его векторная. форма имеет вид: Вектор В случае
Энергия как универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других - переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той иди иной форме) одним телом другому телу, равна энергии, полученной последним телом.
Механическая работа —это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему,зависящая от численной величины и направления силы (сил) и от перемещения точки (точек) тела или системы. Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. выделяют кинетическую энергию поступательного и вращательного движения. СИ — Джоуль. Физический смысл работы Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:
Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:
Поле как форма материи, осуществляющая силовое взаимодействие между телами - поля характеризуются тем, что работа, совершаемая действующими силами при перемещении м.т. из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них– консервативными. Потенциальная энергия — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Диссипация энергии -п ереход части энергии упорядоченных процессов (кинетической энергии движущегося тела, энергии электрического тока и т. п.) в энергию неупорядоченных процессов, в конечном счёте — в теплоту. Если работа, совершаемая силой, зависит от траектории перемещения м.т. из одной точки пространства в другую, то такие тела называются - Диссипативными (рассеивающими);их примером является сила трения. Закон сохранения и превращения энергии- сумма кинетической и потенциальной энергии тел,составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается постоянной. 1.6 Механические колебания - называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t). Периодическими наз. Колебания или значение величин, изменяющихся в процессе колебания повторяются через равные промежутки времени, через который повторяются определенные состояния системы называются периодом (Т, (с))
Уравнение гармонических колебаний.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.4.244 (0.009 с.) |
 ,
,
 - результирующая всех внешних сил, действующих на систему. Это и есть уравнение движения центра масс системы - одно из важнейших уравнений механики. В соответствии с этим уравнением, при движении любой системы частиц ее центр инерции движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы, действующие на систему. При этом ускорение центра инерции совершенно не зависит от точек приложения внешних сил.
- результирующая всех внешних сил, действующих на систему. Это и есть уравнение движения центра масс системы - одно из важнейших уравнений механики. В соответствии с этим уравнением, при движении любой системы частиц ее центр инерции движется так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложены все внешние силы, действующие на систему. При этом ускорение центра инерции совершенно не зависит от точек приложения внешних сил. то
то  а значит,
а значит,  . В инерциальной системе отсчета такой случай реализуется для замкнутой системы. Кроме того, если
. В инерциальной системе отсчета такой случай реализуется для замкнутой системы. Кроме того, если  .
. от времени t, т.е.
от времени t, т.е. 
 и угловое ускорение
и угловое ускорение  .
. тело совершает поворот на угол
тело совершает поворот на угол  , то численно средней угловой скоростью тела за этот промежуток времени будет
, то численно средней угловой скоростью тела за этот промежуток времени будет  . В пределе при
. В пределе при  найдем, что
найдем, что или
или  .
. ,
, — масса малого элемента объёма тела
— масса малого элемента объёма тела  ,
, — плотность,
— плотность, — расстояние от элемента
— расстояние от элемента 
 1.77
1.77


 ; N = R · F · sinα.
; N = R · F · sinα.
 всегда направлен вдоль оси вращения, а
всегда направлен вдоль оси вращения, а  - это составляющая вектора момента силы вдоль оси.
- это составляющая вектора момента силы вдоль оси. 
 получаем
получаем  соответственно и момент импульса относительно оси
соответственно и момент импульса относительно оси  сохраняется. При этом сам вектор L, определенный относительно какой-либо точки на оси вращения, может меняться. Пример такого движения показан на рис. 3.5.
сохраняется. При этом сам вектор L, определенный относительно какой-либо точки на оси вращения, может меняться. Пример такого движения показан на рис. 3.5. Момент импульса
Момент импульса  частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
 где
где  — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,  — импульс частицы.
закон сохранения импульса в замкнутой системе, p=p1+p2=const.
который формулируют так: полный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел этой системы между собой. Иными словами, внутренние силы не могут изменить полного импульса системы ни по модулю, ни по направлению.
1.5 Работа и энергия
Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени.
Работа силы работа
— импульс частицы.
закон сохранения импульса в замкнутой системе, p=p1+p2=const.
который формулируют так: полный импульс замкнутой системы тел остается постоянным при любых взаимодействиях тел этой системы между собой. Иными словами, внутренние силы не могут изменить полного импульса системы ни по модулю, ни по направлению.
1.5 Работа и энергия
Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется во времени.
Работа силы работа 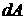 , выполняемая силой
, выполняемая силой  при малом перемещении
при малом перемещении  тела, определяется следующим образом
тела, определяется следующим образом
 , (52) Или
, (52) Или  ,
,
 - угол между направлениями силы и перемещения. Если сила
- угол между направлениями силы и перемещения. Если сила  , то работа силой не совершается, т.к.
, то работа силой не совершается, т.к.  .
Полная работа на пути
.
Полная работа на пути 
 . (53)
Если тело движется прямолинейно и действующая на тело сила
. (53)
Если тело движется прямолинейно и действующая на тело сила  и
и  . (54)
Единица измерения работы
. (54)
Единица измерения работы  Дж (Джоуль).
Дж (Джоуль).
 ,
, 
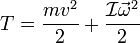 где:
где:  — масса тела
— масса тела  — скорость центра масс тела
— скорость центра масс тела — момент инерции тела
— момент инерции тела  — угловая скорость тела.
— угловая скорость тела. где
где  — ускорение свободного падения,
— ускорение свободного падения,  — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
— высота положения центра масс тела над произвольно выбранным нулевым уровнем.





