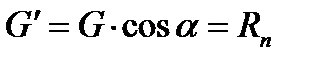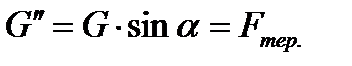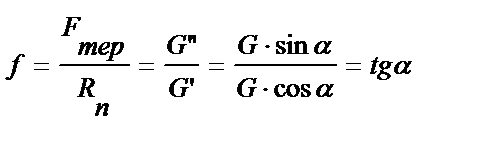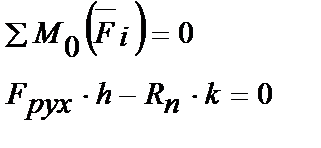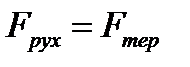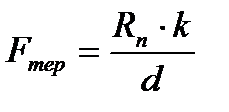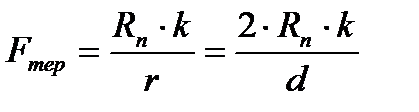Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоска система довільно розміщених сил
Якщо на тіло, закріплене в деякій точці А, діє сила F, то тіло повернеться щодо цієї точки. Обертальний рух тіла характеризується обертаючим моментом М.
де / - плече (перпендикуляр, опущений із точки на лінію дії сили). За одиницю обертаючого моменту приймається 1 Н·м: 1 кH·м = 103 Н·м.
Приведення сили до даної точки полягає в тому, що розглянуту силу М = Мо( Рис. 1.20 Плоскою системою довільно розташованих сил називається система сил, лінії дії яких лежать в одній площині, але не перетинаються в одній точці (рис. 1.21).
Рис. 1.21 Для того щоб привести дану систему довільно розташованих сил до довільно вибраної точці О (див. рис. 1.21), необхідно: - перенести по черзі кожну силу в цю точку; - зрівноважити сили ( У результаті приведення сил (
Цю знову отриману систему збіжних сил (1.1) замінюємо рівнодійною силою, яка дорівнює геометричній сумі даних сил і називається головним вектором системи:
У результаті приведення одержали ще одну систему пар сил
моменти яких дорівнюють моментам даних сил щодо точки О, тобто
Знову отриману систему пар сил (1.2) замінимо однією рівнодійною парою, момент якої дорівнює алгебраїчній сумі моментів доданків пар сил і називається головним моментом системи:
Таким чином, для того щоб тіло під дією плоскої системи довільно розташованих сил перебувало в рівновазі, необхідно, щоб головний вектор і головний момент системи мали дорівнювати нулю:
Виразивши головний вектор знову отриманої системи збіжних сил в аналітичній формі, отримуємо два рівняння рівноваги:
Головний момент системи замінимо алгебраїчною сумою моментів даних сил щодо точки приведення:
Таким чином, одержуємо умову рівноваги плоскої системи довільно розташованих сил: алгебраїчна сума проекцій усіх сил на вісі X та Y повинна дорівнювати нулю та алгебраїчна сума моментів усіх сил відносно точки приведення повинна дорівнювати нулю, тобто
- перша (основна) форма рівняння рівноваги
- друга форма
-третя форма
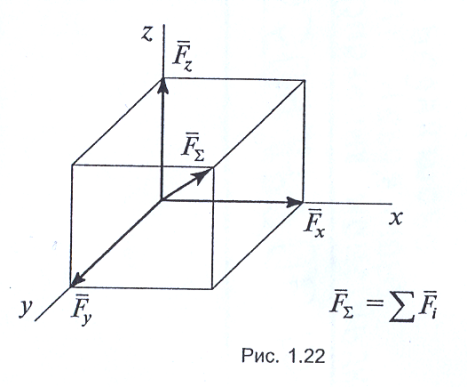
Просторовою системою збіжних сил називається система сил, лінії дії яких не лежать в одній площині, але перетинаються в одній точці. Рівнодійна такої системи сил зображується діагоналлю прямокутного паралелепіпеда, побудованого на цих силах як на сторонах (рис. 1.22). Умова рівноваги просторової системи збіжних сил: алгебраїчна сума проекцій всіх сил на три взаємно перпендикулярні вісі координат повинні дорівнювати нулю, тобто
Для того щоб знайти момент сили
Рис. 1.23
Просторовою системою довільно розташованих сил називається система сил, лінії дії яких не лежать в одній площині й не перетинаються в одній точці. Рівнодійна такої системи сил також дорівнює геометричній сумі цих сил, але зображується діагоналлю складних об'ємних фігур (тетраедр, октаедр і т.д.). Умова рівноваги просторової системи довільно розташованих сил: алгебраїчна сума проекцій всіх сил на три взаємно перпендикулярні вісі координат повинна дорівнювати нулю й алгебраїчній сумі моментів всіх сил щодо тих же осей координат повинна бити дорівнювати нулю, тобто
Тертя Тертям називається опір руху тіла. Сила, з якою тіло чинить опір руху називається силою тертя. Сила тертя завжди напрямлена убік, п р о т и л е ж н у руху. Сила тертя залежить від матеріалу тертьові тіла, чистоти обробки й наявності змащення, й не залежить від величини тертьових поверхонь.
Тертя буває: сухе, напіврідке, рідке. Розрізняють тертя спокою, руху, ковзання й качання. Сила тертя спокою більше, ніж сила тертя руху.
де f - коефіцієнт тертя ковзання.
Матеріали, що володіють дуже малим тертям, називаються антифрикційними (бабіт, бронза, графіт). Застосовуються для виготовлення підшипників і ін.
При змащенні поверхні ковзання тіло починає рухатися з меншим тертям. Розкладемо силу ваги G на складені
Коефіцієнт тертя ковзання
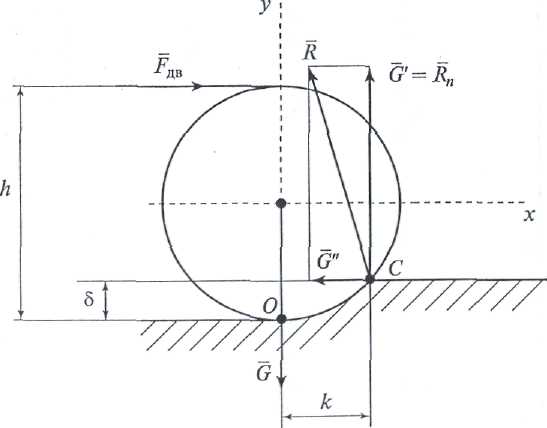
Тертя катання викликано деформацією поверхні котіння. Поверхня, по якій кається ковзанка, деформується на величину δ (рис. 1.27). Деформується й саме тіло, що котиться (наприклад, колесо автомобіля).
Рис.1.27
Складемо рівняння рівноваги:
де h - відстань від поверхні до лінії дії сили; k - коефіцієнт тертя катання. Він дорівнює відрізку ОС (див. рис. 1.27). Тому що Так як
То
Якщо h = d
Якщо h = r
|
||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2089; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.145.114 (0.025 с.) |
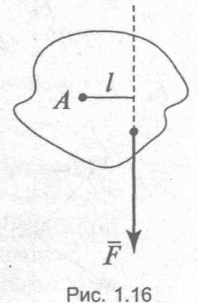 Моментом сили
Моментом сили 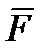 відносно точки А називається величина, чисельно рівна добутку сили на плече (рис. 1.16):
відносно точки А називається величина, чисельно рівна добутку сили на плече (рис. 1.16):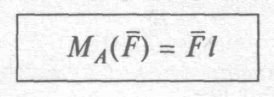
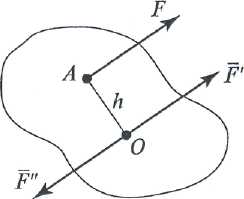
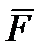 переносять паралельно самій собі в довільно обрану точку О. Для того щоб механічний стан тіла не змінився, силу
переносять паралельно самій собі в довільно обрану точку О. Для того щоб механічний стан тіла не змінився, силу 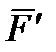 урівноважують силою
урівноважують силою 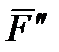 . У результаті приведення сили
. У результаті приведення сили 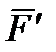 , рівній і паралельній даній силі
, рівній і паралельній даній силі 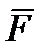 , і пари сил (
, і пари сил (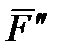 ), момент якої дорівнює моменту даної сили
), момент якої дорівнює моменту даної сили 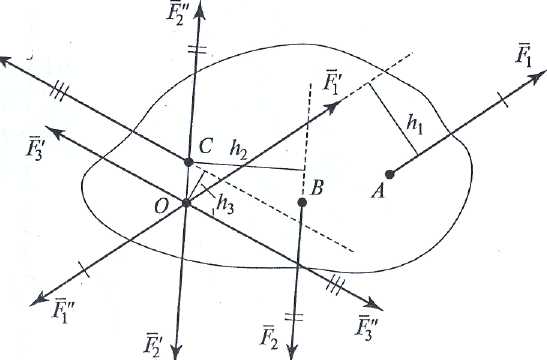
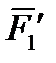 ,
, 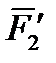 ,
, 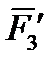 ) силами (
) силами ( ,
, 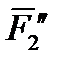 ,
, 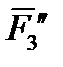 ).
).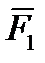 ,
, 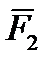 ,
, 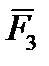 ) до точки О одержали нову систему сил, що складається із плоскої системи збіжних сил (
) до точки О одержали нову систему сил, що складається із плоскої системи збіжних сил (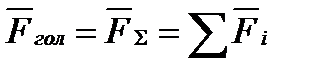
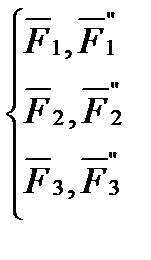 (1.2)
(1.2)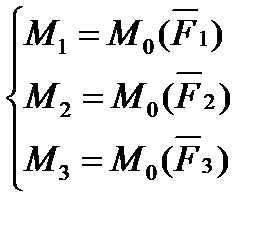
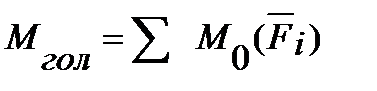
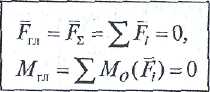
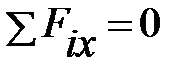 ;
; 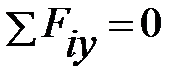
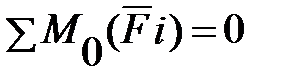
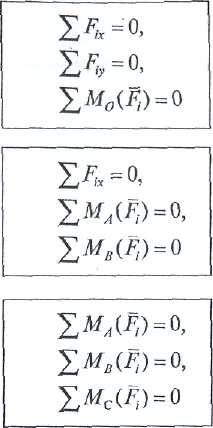
 1.2.4 Просторова система сил
1.2.4 Просторова система сил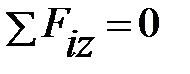
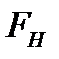 щодо точки О, що є точкою перетини площини Н з віссю z. Момент проекцій
щодо точки О, що є точкою перетини площини Н з віссю z. Момент проекцій 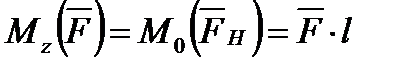
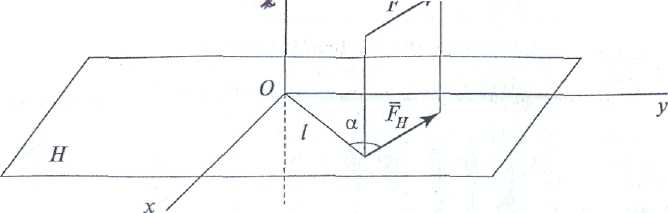
 Моменти сил, перпендикулярних або паралельних осі z, будуть дорівнювати нулю (рис. 1.24).
Моменти сил, перпендикулярних або паралельних осі z, будуть дорівнювати нулю (рис. 1.24).
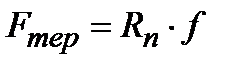 Сила тертя дорівнює добутку сили нормального тиску на коефіцієнт тертя ковзання (рис. 1.25):
Сила тертя дорівнює добутку сили нормального тиску на коефіцієнт тертя ковзання (рис. 1.25):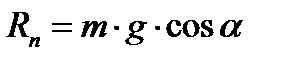 - сила нормального тиску;
- сила нормального тиску;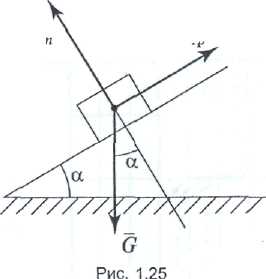 Коефіцієнтом тертя ковзання називається відношення сили тертя до сили нормального тиску:
Коефіцієнтом тертя ковзання називається відношення сили тертя до сили нормального тиску:
 Матеріали, що володіють великим тертям, називаються фрикційними (спеціальні пластмаси із застосуванням азбесту й міді). Застосовуються для накладок гальмових колодок, для накладок дисків зчеплення.
Матеріали, що володіють великим тертям, називаються фрикційними (спеціальні пластмаси із застосуванням азбесту й міді). Застосовуються для накладок гальмових колодок, для накладок дисків зчеплення.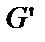 та
та 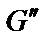 (рис. 1.26):
(рис. 1.26):