
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні поняття та аксіоми статикиСтр 1 из 4Следующая ⇒
Передмова Технічна механіка є фундаментальною загальнотехнічною дисципліною, невід’ємною складовою системи підготовки інженерно-технічних працівників. Під час вивчення курсу студенти оволодівають знаннями законів рівноваги та руху матеріальних тіл, методів розрахунку елементів конструкцій, машин та споруд на міцність, жорсткість, стійкість, основами проектування деталей, вузлів машин. Знання дисципліни необхідні спеціалістам, які повинні організовувати належну експлуатацію й обслуговування сучасної залізничної техніки, удосконалювати її конструкцію та технології застосування. Навчальна дисципліна “Технічна механіка” складається з трьох розділів: теоретична механіка, опір матеріалів, деталі машин. ТЕОРЕТИЧНА МЕХАНІКА Теоретична механіка є науковою основою багатьох сучасних технічних дисциплін. Теоретична механіка – наука про механічний рух матеріальних твердих тіл та їх взаємодії. Механічний рух розуміється як переміщення тіла в просторі та в часі по відношенню до інших тіл, зокрема до Землі. Частковим випадком руху є стан спокою. Під дією навантажень матеріальні тіла змінюють свою форму (деформуються). Однак для наочності та спрощення розв’язування задач теоретичної механіки користуються доволі простими моделями матеріальних тіл такими як матеріальна точка та абсолютно тверде тіло. Матеріальна точка - це умовно прийняте тіло, розмірами якого можна знехтувати в порівнянні з відстанню, на якому воно перебуває. Абсолютно тверде тіло - це умовно прийняте тіло, що не деформується під дією зовнішніх сил. Теоретичну механіку поділяють на статику, кінематику та динаміку. СТАТИКА Основні поняття та аксіоми статики Основним завданням статики є вивчення загальних законів рівноваги матеріальних точок і твердих тіл під дією сил. Для вивчення законів рівноваги статики необхідно знати наступні поняття. Сила — це векторна величина, що характеризує взаємодію між тілами. Дія сили характеризується трьома факторами: точкою прикладення, напрямом, модулем (численним значенням) (рис. 1.1). За одиницю сили приймається 1 Н (Ньютон). 1 кН = 103 Н; 1 МН = 10б Н.
Рис. 1.1
Сили поділяються на зовнішні на внутрішні. Зовнішні сили бувають активні та реактивні. Активні сили викликають переміщення тіла, реактивні прагнуть протистояти переміщенню тіла під дією зовнішніх сил.
Позначення різних типів сил:
Fх, Fу — проекція сили на ось х та у відповідно;
R — реактивна сила; F ∑ - рівнодійна сила. Система сил - це сукупність всіх сил, що діють на тіло (дві або більше сил, які діють на одне тіло). Дві сили або дві системи сили називаються еквівалентними, якщо вони чинять на тіло однакову дію. Рівнодійною називається сила, що чинить таку ж дію на тіло, як і кілька сил, разом взятих. Рівнодійна сила дорівнює геометричній сумі всіх сил, що діють на тіло:
де i = 1,2,3,..., n – черговий номер сили. Зрівноважуючою називається така сила, що дорівнює по величині рівнодійній силі, але направлена в протилежну сторону вона зрівноважує дану систему сил. Основні аксіоми статики
На основі спореження явищ природи були встановлені загальні твердження, що приймаються без доведення – аксіоми статики. В основу статики покладено п'ять аксіом. Перша аксіома (принцип інерції). Система сил, пркладених до матеріальної точки, є зрівноваженою, якшо під дією сил даної системи точка перебуває в стані спокою або рівномірного прямолінійного руху. Матеріальна точка знаходиться в рівновазі, якщо рівнодійна всіх сил, що діють на неї, дорівнює нулю, тобто
Друга аксіома (Принцип рівноваги двох сил). Дві сили, що діють на одне тіло,
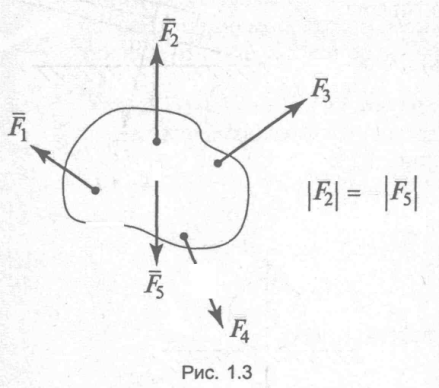
Рис.1.2 взаємно зрівноважені, якщо вони рівні по модулю, протилежні по напряму та лежать на однієї прямій (рис. 1.2). Третя аксіома (принцип приєднання чи виключення взаїмноврівноважених сил) механічний стан тіла не зміниться, якщо до нього чи приєднати чи виключити взаїмноврівноважену систему сил (рис. 1.3).
П’ята аксіома Принцип дії та протидії: сили, з якими два тіла діють одине на одне, дорівнюють по значенню, протилежні по напрямку та лежать на однієї прямій (однак не врівноважені, тому що прикладені до різних тіл) (рис. 1.5).
Пара сил
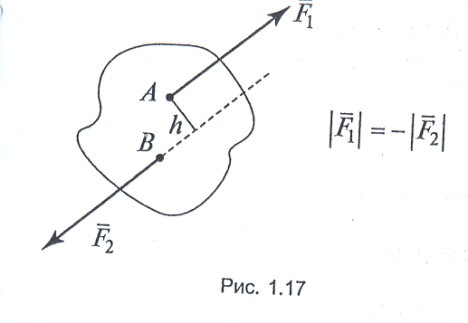
Парою сил називається система двох сил, які дорівнюють по модулю (значенню), протилежні по напрямку та з паралельними лініями дії (не лежачих на однієй прямій) (рис. 1.17).
Обертаючий момент пари сил дорівнює добутку однієї із сил пари на плече:
де h – плече пари сил (перпендикуляр, проведений між лінією дії сил)
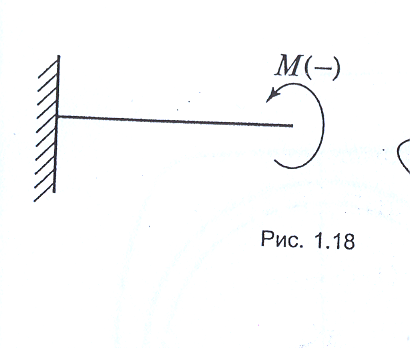
Пари сил на схемах зображуються дугоподібною стрілкою (рис. 1.18).
Рис. 1.19 Дві парі сил називаються еквівалентними, якщо вони виконують на тіло о д н а к о в у дію. У еквівалентних пар сил обертаючі моменти повинні бути однаковими як за величиною, так і за напрямком. Умова рівноваги плоскої системи пар сил: алгебраїчна сума моментів доданків пар сил повинна дорівнювати нулю, тобто
Тертя Тертям називається опір руху тіла. Сила, з якою тіло чинить опір руху називається силою тертя. Сила тертя завжди напрямлена убік, п р о т и л е ж н у руху. Сила тертя залежить від матеріалу тертьові тіла, чистоти обробки й наявності змащення, й не залежить від величини тертьових поверхонь. Тертя буває: сухе, напіврідке, рідке. Розрізняють тертя спокою, руху, ковзання й качання. Сила тертя спокою більше, ніж сила тертя руху.
де f - коефіцієнт тертя ковзання.
Матеріали, що володіють дуже малим тертям, називаються антифрикційними (бабіт, бронза, графіт). Застосовуються для виготовлення підшипників і ін.
При змащенні поверхні ковзання тіло починає рухатися з меншим тертям. Розкладемо силу ваги G на складені
Коефіцієнт тертя ковзання
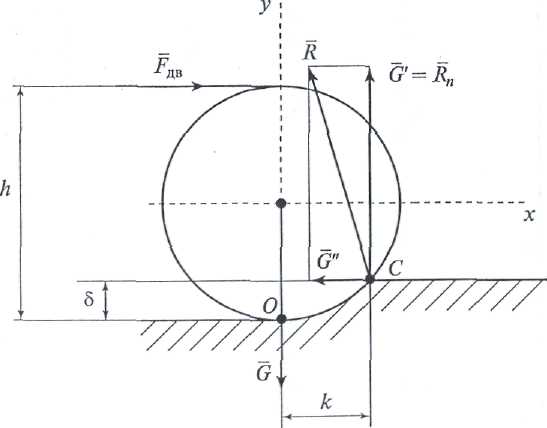
Тертя катання викликано деформацією поверхні котіння. Поверхня, по якій кається ковзанка, деформується на величину δ (рис. 1.27). Деформується й саме тіло, що котиться (наприклад, колесо автомобіля).
Рис.1.27
Складемо рівняння рівноваги:
де h - відстань від поверхні до лінії дії сили; k - коефіцієнт тертя катання. Він дорівнює відрізку ОС (див. рис. 1.27). Тому що Так як
То
Якщо h = d
Якщо h = r
Тема 6. Центри ваги Сила ваги - це сила, з якої тіло притягається до землі. Центр ваги - це точка прикладання сили ваги (рис. 1.32). Положення центра ваги простих геометричних фігур: 1) у прямокутнику, квадраті, ромбі, паралелограмі – на перетині
діагоналей (рис. 1.33);
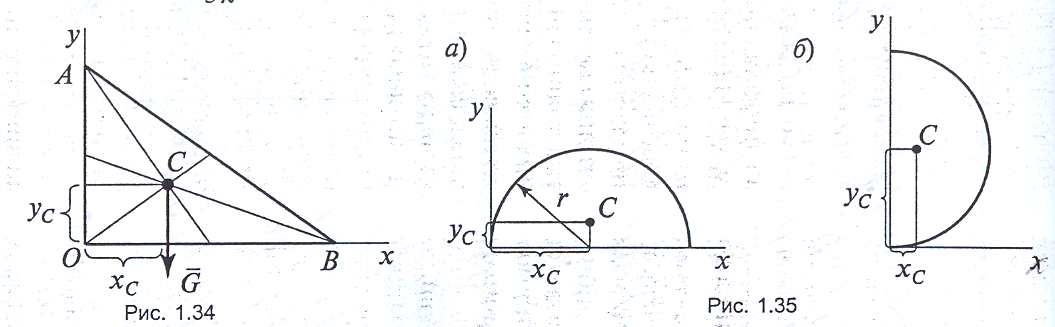
Рис. 1,32 Рис. 1,33 2) у трикутнику – на перетині медіан (рис.1.34)
3) У коловому секторі чи на півколі – у точці з координатами:
4) У конусі чи повній піраміді – на 1/3 висоти від основи (рис. 1.36)
Рис. 1.36
Рис. 1.37
Положення центра ваги плоских фігур прокатних профілів: 1) у балці двотаврової (рис.1.37) у точці з координатами
h - висота двутавра. 2) у швелері (рис.1.38) – у точці з координатами
де h - висота швелера
3) у рівнополочному кутку (рис.1.39) – у точці з координатами
Рис. 1.39
Якщо плоска фігура має неправильну геометричну форму, то центр ваги такої фігури можна визначити двома способами: 1) методом підвішування фігури; 2) теоретичним методом. У цьому випадку плоска фігура розбивається на певну кількість елементарних фігур, що мають правильну геометричну форму. Потім визначається положення центра ваги й площі кожної елементарної фігури. Для того щоб знайти координати центра ваги заданої складної фігури, використовуються наступні формули:
де Ai - площі елементарних фігур, на які розбита складна фігура; хi, уi - координати центра ваги кожної елементарної фігури відносно випадкових вісей х та у.
КІНЕМАТИКА
Тема 3. Складний рух точки У деяких випадках рухомі тіла, які приймаються за матеріальні точки, можуть чинити складний рух (наприклад, рух людиною у вагоні рухаючого потягу). Складний рух точки – це рух точки відносно нерухомої системи координат. Швидкість складного руху називається абсолютною швидкістю. Складний рух точки складається з переносного поперечного руху, тобто рух рухомої системи координат відносно нерухомої (наприклад, рух потягу відносно Землі), та відносного руху, тобто рух точки відносно рухомої системи координат. Таким чином швидкість абсолютного руху точки дорівнює геометричній сумі швидкостей переносного та відносного руху:
Динаміка Рівняння кінетостатики
Розв’язання. 1 Будуємо розрахунково-силову схему (рис. 1.61), тобто показуємо всі сили, що діють на тіло, що рухається. Потім указуємо вісь координат, уздовж якого відбувається рух тіла.
2 Складаємо рівняння кінетостатики та розв’язуємо його відносно невідомої величины FH:
де
Відповідь: FH = 7200 Н.
Рішення. 1. Будуємо розрахунково-силову схему (рис. 1.62). 2. Складаємо рівняння кінетостатики:
де
Відповідь FД= 14 кН.
Та обертальному русі Потужність - це величина, чисельно рівна роботі, зробленої за одиницю часу:
Потужність при поступальному русі
Потужність при обертальному русі
Коефіцієнт корисної дії (ККД) машин і механізмів -це величина, що показує, яка частина від усієї виконаної роботи витрачається корисно:
де Wпол, Wзатр — корисна і витрачена робота; Рпол, Рзатр —корисна і витрачена потужність.
За одиницю потужності приймається 1 Вт: 1 Вт = 1 Дж/с.
Тема 4. Теореми динаміки При поступальному русі теореми динаміки мають наступний вид. Теорема про зміну кількості руху: зміна кількості руху матеріальної точки дорівнює імпульсу деякої сили, прикладеної до цієї точки, тобто
Де Ft - імпульс сили; mv - кількість руху. Доказ:
Теорема про зміну кінетичної енергії: зміна кінетичної енергії матеріальної точки дорівнює роботі деякої сили по переміщенню цієї точки, тобто
Де: W = FS —робота;
Доказ:
Звідки
При обертальному русі теореми динаміки мають наступний вигляд. Теорема про зміну кількості руху: зміна кількості руху твердого тіла дорівнює добутку обертаючого моменту на час його дії, тобто
де І - момент інерції тіла; ω - кутова швидкість.
Теорема про зміну кінетичної енергії: зміна кінетичної енергії твердого тіла дорівнює роботі цього тіла при обертальному русі, тобто
Де W = M φ Передмова Технічна механіка є фундаментальною загальнотехнічною дисципліною, невід’ємною складовою системи підготовки інженерно-технічних працівників. Під час вивчення курсу студенти оволодівають знаннями законів рівноваги та руху матеріальних тіл, методів розрахунку елементів конструкцій, машин та споруд на міцність, жорсткість, стійкість, основами проектування деталей, вузлів машин. Знання дисципліни необхідні спеціалістам, які повинні організовувати належну експлуатацію й обслуговування сучасної залізничної техніки, удосконалювати її конструкцію та технології застосування. Навчальна дисципліна “Технічна механіка” складається з трьох розділів: теоретична механіка, опір матеріалів, деталі машин. ТЕОРЕТИЧНА МЕХАНІКА Теоретична механіка є науковою основою багатьох сучасних технічних дисциплін. Теоретична механіка – наука про механічний рух матеріальних твердих тіл та їх взаємодії. Механічний рух розуміється як переміщення тіла в просторі та в часі по відношенню до інших тіл, зокрема до Землі. Частковим випадком руху є стан спокою.
Під дією навантажень матеріальні тіла змінюють свою форму (деформуються). Однак для наочності та спрощення розв’язування задач теоретичної механіки користуються доволі простими моделями матеріальних тіл такими як матеріальна точка та абсолютно тверде тіло. Матеріальна точка - це умовно прийняте тіло, розмірами якого можна знехтувати в порівнянні з відстанню, на якому воно перебуває. Абсолютно тверде тіло - це умовно прийняте тіло, що не деформується під дією зовнішніх сил. Теоретичну механіку поділяють на статику, кінематику та динаміку. СТАТИКА Основні поняття та аксіоми статики Основним завданням статики є вивчення загальних законів рівноваги матеріальних точок і твердих тіл під дією сил. Для вивчення законів рівноваги статики необхідно знати наступні поняття. Сила — це векторна величина, що характеризує взаємодію між тілами. Дія сили характеризується трьома факторами: точкою прикладення, напрямом, модулем (численним значенням) (рис. 1.1). За одиницю сили приймається 1 Н (Ньютон). 1 кН = 103 Н; 1 МН = 10б Н.
Рис. 1.1
Сили поділяються на зовнішні на внутрішні. Зовнішні сили бувають активні та реактивні. Активні сили викликають переміщення тіла, реактивні прагнуть протистояти переміщенню тіла під дією зовнішніх сил. Позначення різних типів сил:
Fх, Fу — проекція сили на ось х та у відповідно;
R — реактивна сила; F ∑ - рівнодійна сила. Система сил - це сукупність всіх сил, що діють на тіло (дві або більше сил, які діють на одне тіло). Дві сили або дві системи сили називаються еквівалентними, якщо вони чинять на тіло однакову дію. Рівнодійною називається сила, що чинить таку ж дію на тіло, як і кілька сил, разом взятих. Рівнодійна сила дорівнює геометричній сумі всіх сил, що діють на тіло:
де i = 1,2,3,..., n – черговий номер сили. Зрівноважуючою називається така сила, що дорівнює по величині рівнодійній силі, але направлена в протилежну сторону вона зрівноважує дану систему сил. Основні аксіоми статики
На основі спореження явищ природи були встановлені загальні твердження, що приймаються без доведення – аксіоми статики. В основу статики покладено п'ять аксіом. Перша аксіома (принцип інерції). Система сил, пркладених до матеріальної точки, є зрівноваженою, якшо під дією сил даної системи точка перебуває в стані спокою або рівномірного прямолінійного руху. Матеріальна точка знаходиться в рівновазі, якщо рівнодійна всіх сил, що діють на неї, дорівнює нулю, тобто
Друга аксіома (Принцип рівноваги двох сил). Дві сили, що діють на одне тіло,
Рис.1.2 взаємно зрівноважені, якщо вони рівні по модулю, протилежні по напряму та лежать на однієї прямій (рис. 1.2). Третя аксіома (принцип приєднання чи виключення взаїмноврівноважених сил) механічний стан тіла не зміниться, якщо до нього чи приєднати чи виключити взаїмноврівноважену систему сил (рис. 1.3).
П’ята аксіома Принцип дії та протидії: сили, з якими два тіла діють одине на одне, дорівнюють по значенню, протилежні по напрямку та лежать на однієї прямій (однак не врівноважені, тому що прикладені до різних тіл) (рис. 1.5).
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 983; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.183.24 (0.166 с.) |

 — зовнішня сила;
— зовнішня сила;




 Четверта аксіома (принцип паралелограма). Рівнодійна двох сил, прикладених до тіла в одній точці та спрямованих одна до одної під кутом, дорівнює геометричній сумі цих сил і зображується діагоналлю паралелограма, побудованого на цих силах як на сторонах (рис. 1.4).
Четверта аксіома (принцип паралелограма). Рівнодійна двох сил, прикладених до тіла в одній точці та спрямованих одна до одної під кутом, дорівнює геометричній сумі цих сил і зображується діагоналлю паралелограма, побудованого на цих силах як на сторонах (рис. 1.4).
 Пара сил робить на тіло обертаючу дію, що характеризується обертаючим моментом М.
Пара сил робить на тіло обертаючу дію, що характеризується обертаючим моментом М.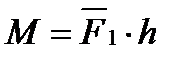
 Пари сил н е м о ж н а замінити однією рівнодійною силою. Пари сил н е м а є проекцій на вісі координат(проекція пари сил на ось - нуль). Якщо на тіло діє декілька пар сил, то їх можна замінити однією рівнодійною парою, момент якої дорівнює алгебраїчній сумі моментів доданків пар сил, що діють на тіло (рис. 1.19):
Пари сил н е м о ж н а замінити однією рівнодійною силою. Пари сил н е м а є проекцій на вісі координат(проекція пари сил на ось - нуль). Якщо на тіло діє декілька пар сил, то їх можна замінити однією рівнодійною парою, момент якої дорівнює алгебраїчній сумі моментів доданків пар сил, що діють на тіло (рис. 1.19):


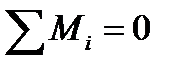
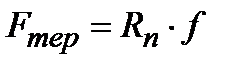 Сила тертя дорівнює добутку сили нормального тиску на коефіцієнт тертя ковзання (рис. 1.25):
Сила тертя дорівнює добутку сили нормального тиску на коефіцієнт тертя ковзання (рис. 1.25):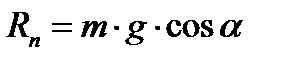 - сила нормального тиску;
- сила нормального тиску;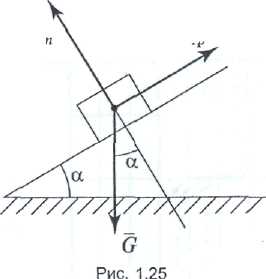 Коефіцієнтом тертя ковзання називається відношення сили тертя до сили нормального тиску:
Коефіцієнтом тертя ковзання називається відношення сили тертя до сили нормального тиску:
 Матеріали, що володіють великим тертям, називаються фрикційними (спеціальні пластмаси із застосуванням азбесту й міді). Застосовуються для накладок гальмових колодок, для накладок дисків зчеплення.
Матеріали, що володіють великим тертям, називаються фрикційними (спеціальні пластмаси із застосуванням азбесту й міді). Застосовуються для накладок гальмових колодок, для накладок дисків зчеплення.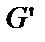 та
та 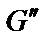 (рис. 1.26):
(рис. 1.26):
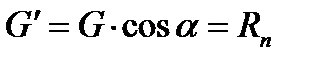
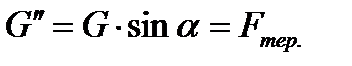
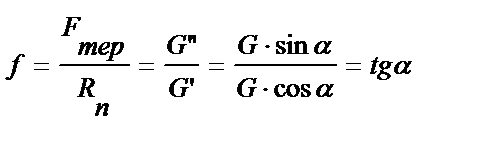
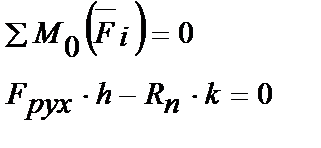
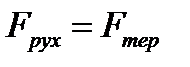

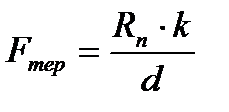
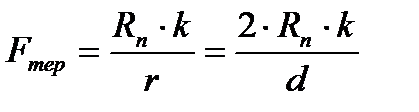











 - відстань від центра ваги та
- відстань від центра ваги та  до зовнішньої грані стінки
до зовнішньої грані стінки



 (теорема складання швидкостей)
(теорема складання швидкостей)
 Задача 2. Вантаж масою 900 кг, підвішений на тросі, опускається вертикально вниз із прискоренням 2 м/с2. Знайти натяг троса, зневажаючи його власною масою.
Задача 2. Вантаж масою 900 кг, підвішений на тросі, опускається вертикально вниз із прискоренням 2 м/с2. Знайти натяг троса, зневажаючи його власною масою.


 Маємо
Маємо звідки
звідки Задача 3. Автомобіль масою 1600 кг рухається по мосту з постійною швидкістю 90 км/ч. Визначити силу тиску автомобіля на міст, якщо r = 500 м.
Задача 3. Автомобіль масою 1600 кг рухається по мосту з постійною швидкістю 90 км/ч. Визначити силу тиску автомобіля на міст, якщо r = 500 м.


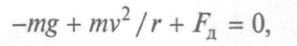 маємо
маємо звідки
звідки


 Якщо α = 0, то
Якщо α = 0, то



 звідки
звідки .
.
 — кінетична енергія.
— кінетична енергія.






