
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение температурных переходов в полимерах методом ДСК
В полимерах, если идти от низких температур к высоким, происходит последовательное „размораживание“ различных форм молекулярной подвижности. Среди ряда таких релаксационных переходов выделяют два основных и характерных для всех полимеров, называемых: β-переходы и α-переходы. β-переходы — это движение отдельных сравнительно небольших участков цепных молекул. Эффективное развитие такой β-релаксации происходит при соответствующей температуре Tβ. α-переходы — это движение более крупных участков молекул-сегментов, кооперированное с движением сегментов соседних молекул. Наступление этих переходов характеризуется температурой Tα, носящей название «температура стеклования (расстекловывания)», поскольку именно в области Tα происходит переход полимера из стеклообразного в высокоэластическое состояние. Можно считать, что β–релаксация подготавливает α-релаксацию. И β- и α-переходы осуществляются локальными флуктуациями энергии, за счет которых преодолеваются барьеры в элементарных актах переходов: Uβ и Uα. Широко распространенная характеристика релаксационных процессов — энергия активации и есть величина этих барьеров. Знание энергии активации имеет важное физическое значение, поскольку позволяет строить модели элементарных актов процессов. Поэтому корректное определение энергии активации β- и α-переходов из экспериментальных данных является серьезной физической задачей. Среди многих методов исследования релаксационных процессов (механическая, диэлектрическая, акустическая спектроскопия, дифрактометрия и др.) видное место занимает дифференциальная сканирующая калориметрия (ДСК) [3]. Получаемая методом ДСК информация о температурной зависимости теплоемкости объекта [Cp(T)] позволяет регистрировать релаксационные переходы и определять их характеристики. Так, включение с ростом температуры „замороженных“ до этого различных форм молекулярной подвижности в полимерах проявляется в виде немонотонностей зависимости Cp(T) (рис. 1.5.1). Релаксационная природа и α- и β-переходов ярко проявляется в том, что их положение по температуре зависит от скорости изменения температуры: VT = dT/dt (3.2.1) — скорости сканирования. При увеличении VT температуры, Tβ и Tα возрастают (рис. 1.5.1). Именно из зависимостей Tβ(VT) и Tα(VT) извлекаются значения энергии активации переходов. Распространенным является построение зависимостей в форме lnVT(1=Tβ) и lnVT(1=Tα). Из наклонов этих зависимостей определяется величина:
Uf = −k(∆ lnVT/∆(1=Ti)), (3.2.2) которой часто присваивают название „энергии активации“ (k = 8.6 10-5 eV/K — постоянная Больцмана) [3].
Рис. 3.2.1. Схема температурной зависимости теплоемкости полимеров. I — область β-релаксации, II — область α-релаксации. 1 — скорость сканирования
Ввиду того что при измерениях диапазон изменения VT, как правило, невелик (около одного десятичного порядка), то зависимости lnVT (1=Ti) оказываются близкими к линейным, что выдвигается аргументов в пользу применимости данного способа определения энергии активации [3]. Кристаллизация гибкоцепных полимеров в обычных условиях — из невозмущенных расплавов или растворов — приводит, как правило, к образованию пластинчатых кристаллов — ламелей со сложенными цепями, толщина которых (≈ 10-102 нм) на порядки меньше поперечных размеров и зависит от ряда условий, особенно от термической предыстории. Во всех случаях кристаллизация идет не нацело и в полимере сохраняются неупорядоченные области; это и определяет особенности термодинамики плавления частично кристаллических полимеров [2]. Создание метода ДСК привело к качественному скачку в экспериментальных возможностях количественного анализа и описания фазового перехода плавления полимеров, оценки его термодинамических параметров, характеристик полимерных кристаллов и их поверхности. С помощью ДСК удается определять: - истинные температуры плавления полимеров - истинные интервалы плавления - энтальпии плавления частично кристаллических полимеров При анализе следует различать три температуры плавления: экспериментальную Тпл, полученную при данной скорости нагревания ν и отвечающую максимуму эндотермического пика плавления; истинную, физическую температуру
Наиболее фундаментальной из них является температура
где γi относится к свободной поверхностной энергии торцевых граней, у которых происходит складывание цепей, а ρk – плотность кристалла [2]. При оценке Перегревом кристаллов называют наблюдаемое завышение Тпл, тем большее, чем выше скорость нагревания ν; оно особенно существенно при ν ≈ 20 — 40 град/мин и выше (рис. 3.2.2). Нередко оказывается, что экспериментальная Тпл >
Рис 3.2.2. Эндотермические пики плавления аморфно-кристаллического полимера (
С другой стороны, в ходе нагревания метастабильных ламелей при малых ν структурная реорганизация и (или) рекристаллизация приводит к их утолщению и, вследствие этого, также к завышению температур Тпл, фактически относящихся уже не к исходным, а к преобразованным в ходе опыта кристаллам. Ввиду этого, использование одной низкой скорости нагревания с целью предотвращения эффекта перегрева также в общем случае некорректно [2]. Плавление как фазовый переход первого рода характеризуется скачкообразным приращением основных термодинамических характеристик — энтальпии Н, энтропии S, объема V. Равновесная температура плавления полимерных кристаллов определяется их энтальпией и энтропией плавления:
Согласно Флори, величина
В отличие от низкомолекулярных кристаллов, энтропия плавления которых определяется нарушениями позиционного и ориентационного порядка (∆Sпл=∆Sор + ∆Sпоз), для кристаллов гибкоцепных линейных полимеров: ∆Sпл=∆Sор + ∆Sпоз+∆Sконф (3.2.5) и основной вклад вносит компонента, обусловленная изменением конформации цепей при плавлении кристаллов, (∆Sконф ≈(0,75 ± 0,1) ∆Sпл) [2]. Ее значение возрастает с повышением гибкости цепей и мало для жестких макро молекул, (∆Sконф ~ σ-2),где σ — параметр их равновесной жесткости. Отсюда проистекает и известная закономерность: температура Поскольку кривая ДСК фиксирует зависимость теплового потока от температуры dH/dt(T) или, в условиях ν= const, от времени dH/dt(t), измерение площади эндотермического пика плавления (заштрихована на рис. 3.2.2) позволяет непосредственно определять энтальпию плавления полимера ∆ H пл. Выбор скорости нагревания при этом не существен: она влияет только на форму пика, а не на его площадь. Важным здесь является лишь корректное проведение базовой линии, от которой ведется отсчет площади пика [2].
|
|||||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 1164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.181.209 (0.014 с.) |
 , 2 — скорость сканирования T” >
, 2 — скорость сканирования T” > 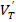 [3. с 87].
[3. с 87]. и равновесные температуры плавления полимерных кристаллов
и равновесные температуры плавления полимерных кристаллов  ,
,
 и на этой основе параметр внутрицепной кооперативности плавления ν;
и на этой основе параметр внутрицепной кооперативности плавления ν; , полимерных кристаллов
, полимерных кристаллов  , и на этой основе — степень кристалличности полимеров.
, и на этой основе — степень кристалличности полимеров. для данной кристаллической структуры полимера и равновесную температуру плавления совершенного кристалла
для данной кристаллической структуры полимера и равновесную температуру плавления совершенного кристалла  и отклонение
и отклонение  (3.2.3)
(3.2.3)  необходимо исходить из истинных температур плавления кристаллов данного размера
необходимо исходить из истинных температур плавления кристаллов данного размера  , как правило, не совпадающих с экспериментальной Тпл, измеренной при ν = const. Расхождение между Тпл и
, как правило, не совпадающих с экспериментальной Тпл, измеренной при ν = const. Расхождение между Тпл и 
 w = 7 · 104) при ν = 0,31 (1), 0,62 (2), 1,25 (3), 2.5 (4), 5 (5), 10 (6), 20 (7) и 40 (8) град/мин [2, c. 142].
w = 7 · 104) при ν = 0,31 (1), 0,62 (2), 1,25 (3), 2.5 (4), 5 (5), 10 (6), 20 (7) и 40 (8) град/мин [2, c. 142]. (3.2.4)
(3.2.4) включает две составляющие, одна из которых связана с нарушением межмолекулярного порядка, определяется изменением энергии ММВ, зависит от энергии когезии Ек, а другая — внутримолекулярная, контролируемая, например, переходом от вытянутой конформации в кристалле к статистическому клубку в расплаве; она связана с ростом числа высокоэнергетических G-конформаций. Вклад второй компоненты в случае ПЭ не превышает 0,25
включает две составляющие, одна из которых связана с нарушением межмолекулярного порядка, определяется изменением энергии ММВ, зависит от энергии когезии Ек, а другая — внутримолекулярная, контролируемая, например, переходом от вытянутой конформации в кристалле к статистическому клубку в расплаве; она связана с ростом числа высокоэнергетических G-конформаций. Вклад второй компоненты в случае ПЭ не превышает 0,25  ) и жесткость цепей (меньше ∆Sпл). Следовательно, для плавления наблюдается качественно такая же зависимость от этих основных молекулярных характеристик, что и для основных (α и β) релаксационных переходов [2].
) и жесткость цепей (меньше ∆Sпл). Следовательно, для плавления наблюдается качественно такая же зависимость от этих основных молекулярных характеристик, что и для основных (α и β) релаксационных переходов [2].


