
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок визначення страхових тарифів.
Виходячи з того, що ціна страхового продукту складається з двох частин: тарифу-нетто і навантаження — перша з яких пов'язана з настанням страхової події, а друга — не пов'язана з нею і призначена для утримання страхової компанії, кожен із цих елементів розраховується окремо, а потім їхні величини, переважно в абсолютному (грошовому) виразі додаються. Можливе безпосереднє визначення тарифу-нетто і навантаження у відносних показниках (відсотках або проміле) до страхової суми, після чого обидв частини додаються, і тариф- брутто виражається у відсотках чи проміле. Переважно у відносних показниках встановлюються страхові тарифи-брутто з ризикового страхування. При страхуванні життя можливі два варіанти: 1) встановлення страхових тарифів-брутто у грошовому виразі на одну тисячу гривень страхової суми; 2) розділене (відокремлене) встановлення тарифів-нетто у грошовому виразі на одну тисячу гривень страхової суми і навантаження у відсотках до загального страхового тарифу. Тоді загальну величину тарифу-брутто визначає агент або брокер при укладенні договору страхування. Для цього застосовується формула ТБ = (ТН * 100)/(100 - Н), де ТБ – тариф-брутто, ТН – тариф-нетто, Н – питома вага навантаження в тарифі-брутто. За структурою тарифної ставки-нетто страхові тарифи бувають одно- та багатопредметні (ризикові). При страхуванні життя останні мають ще один різновид — опційні, при яких до одного-двох основних ризиків страхувальник згідно зі своїми потребами добирає додаткові ризики (опції), укладаючи для цього доповнення до чинного договору страхування 19. Тарифна політика в галузі страхування. Під тарифною політикою розуміється цілеспрямована діяльність страховика із встановлення, уточнення і упорядкування страхових тарифів на користь успішного й беззбиткового розвитку страхування. Вона базується на наступних принципах: 1. Еквівалентність страхових стосунків сторін. Це означає, що нетто-ставки повинні максимально відповідати вірогідності збитку. Тим самим забезпечується зворотність засобів страхового фонду за тарифний період тієї сукупності страхувальників, в масштабі якої будувалися страхові тарифи. 2. Доступність страхових тарифів для широкого кола страхувальників. Надмірно високі тарифні ставки є гальмом на шляху розвитку страхування. Доступність тарифних ставок знаходиться у прямій залежності від числа страхувальників і кількості застрахованих об'єктів.
3. Стабільність розмірів страхових тарифів протягом довгого часу. Якщо тарифні ставки залишаються незмінними протягом багатьох років, у страхувальників зміцнюється тверда впевненість в солідності страхової справи. Підвищення тарифних ставок можливе лише при неухильному зростанні збитковості страхової суми в цілях забезпечення беззбиткового проведення страхування. 4. Розширення обсягу страхової відповідальності, якщо це дозволяють тарифні ставки. Дотримання даного принципу є пріоритетним напрямом в діяльності страховика, оскільки чим ширше обсяг страхової відповідальності, тим більше страхування відповідає потребам страхувальників 5. Забезпечення самоокуповності і рентабельності страхових операцій. Страхові тарифи повинні будуватися так, щоб надходження страхових платежів постійно покривало витрати страховика і навіть забезпечувало деяке перевищення доходів над витратами (прибуток страховика).
20. Принципи диференціації страхових тарифів. Добровільне страхування через його вибірковість обумовлює необхідність диференціації тарифної ставки. За основу повинні братися відмінності у величині не тільки нетто-ставки, але і надбавки. За добровільним страхуванням різних об'єктів диференціація тарифних ставок побудована по територіях, видах страхування, однорідних об'єктах страхування. Територіальна диференціація враховує відмінності в рівні збитковості страхової суми на селі і в містах, що пов'язане в основному з вищими показниками загоряння будівель у сільській місцевості. Ці показники роблять також вплив на диференціацію тарифів залежно від вогнестійкості будов у господарствах громадян. По страхуванню тварин диференціація тарифів враховує відмінності в показниках збитковості по видах тварин (великій рогатій худобі, вівцях і козах, свинях, конях і т.д.), їх вікових групах. При страхуванні засобів транспорту, належних громадянам, диференціація тарифних ставок відображає відмінності міри ризику окремих видів транспорту: автомобілів, мотоциклів, мопедів, моторних човнів і т.п.
Тут застосовується диференціація, стимулююча страхування засобів транспорту в повній вартості. У багатьох країнах диференціація тарифів по страхуванню засобів транспорту враховує і такі критерії, що впливають на збитковість страхової суми, як марки автомобілів, водійський стаж страхувальника та ін.. Диференціація страхових тарифів є дієвим науково обґрунтованим інструментом розподілу збитку, що відображає оптимальну участь кожного страхувальника у формуванні страхового фонду.
21. Загальні поняття про зміну вартості грошей. Вартість грошей як товару з часом змінюється. Зміна їхньої вартості означає, що за одну і ту ж суму грошей через певний проміжок часу можна купити більшу або меншу кількість товарів, ніж у теперішній час. Таким чином, на гроші впливають фактори двох типів — одні підвищують, другі зменшують їхню вартість. Основними факторами зменшення вартості грошей є: 1) Інфляція в першу чергу пов'язується із загальним підвищенням цін. 2) Ризиковість операцій зумовлюється кількома факторами. У першу чергу сюди належать загальні ризики здійснення операцій купівлі-продажу і отримання виручки — втрата товарів, зміна цін, зміна політичної обстановки та ін. У другу чергу сюди належать складність сучасного виробництва і швидкість змін у виробничих технологіях, яка зумовлює ймовірність зазнати невдачі, краху і банкрутства. 3) Здатність до ліквідності полягає в можливостях перетворити куплені або створені цінності знову в гроші, наприклад, продати готову продукцію, нерухомість, підприємства, житлові будинки і т. д. По суті справи, при використанні грошей можна спостерігати два процеси: першим є зростання їхньої вартості під впливом процентів, доходів, прибутку, другим є зменшення їхньої вартості під впливом інфляції, ризиковості і здатності до ліквідності. З певною вірогідністю можна ствердити, що іде алгебраїчне додавання величин цих двох факторів, і якщо переважає позитивний фактор, то вартість грошей зростає, а якщо негативний — то зменшується.
22. Способи визначення теперішньої вартості грошей. Bизначимо теперішню вартість капіталу, знаючи його кінцеву (майбутню) вартість. Такий процес називається дисконтуванням, а різниця між кінцевою (FV) і початковою (PV) вартістю називається дисконтом (D). Таким чином, D = FV – PV і PV можна вважати теперішньою, або здисконтованою вартістю майбутнього капіталу FV. Виходячи з того, що дисконтування є оберненою операцією до опроцентування, формули простого і складного процента застосовуються для визначення простого і складного дисконта. З формули простого процента виводиться формула простого дисконта PV1. PV1= FV1/(1 +i*n) а якщо FV1 винести за дужки, отримаємо PV1 = FV1*(1 + i · n)^(-1). (2.3.) Вираз (1 + i · n)^(-1) називається простим дисконтним множником і переважно позначається буквою vn або v. Подібно виводиться формула складного дисконта РV2. Із формули складного процента FV2 =PV(1 + i)^n маємо PV2= FV2/((1 + i)^n) а винісши FV2 за дужки, отримаємо PV2 = FV2(1 + i)^(-n). (4) Вираз (1 + i)^(-n) називається складним дисконтним множником і переважно позначається буквою vn.
Виведемо ще одну формулу для визначення теперішньої вартості грошей на підставі процентної величини дисконта d. Цей показник визначається аналогічно величині процента за формулою d = D/ FV (5)
23. Способи визначення майбутньої вартості грошей. Для визначення майбутньої вартості грошей застосовується показник норми доходності у вигляді процента. Знаючи вкладену (інвестовану) суму грошей і норму доходності, можна визначити майбутню вартість грошей. Такий процес називається опроцентуванням, а різновидів процента є два: простий і складний. Простий процент – це нарахування відсотку лише на початково інвестовану суму FV1 = PV + PV·i·n = P(1 + i·n), (1.) де: PV — початкова сума вкладу; i — норма доходності у відсотках; п — період вкладення, роки. Якщо ж вкладник (інвестор) не вилучатиме щорічний доход, то він буде приєднуватися до початкової суми і завдяки цьому відбуватиметься щорічне зростання (капіталізація) вкладеної суми. Таке збільшення називається складним процентом або майбутньою вартістю за складним процентом (FV2) і визначається за формулою FV2=PV(1 + i)^n, (2.) де: PV — початкова сума вкладу; і — норма доходності у відсотках; п — період вкладення, роки. В формулах 1. і 2. показники простого і складного процента можна замінити показником майбутньої вартості грошей (FV). Отже, за допомогою опроцентування (у першу чергу складного) можна визначити майбутню вартість грошей, тобто збільшення капіталу внаслідок приєднання до нього додаткового (інвестиційного) доходу.
24. Відсотки. Відсоткові ставки. Одним з головних показників у фінансових розрахунках є відсоток, під яким розуміють абсолютну величину доходів від грошей, наданих у борг у будь-якій їх формі Під відсотковою ставкою розуміють відношення відсоткових грошей, які виплачуються за фіксований відрізок часу, до величини позички. Відсоткова ставка виконує функції вимірювача ступеня дохідності фінансових операцій незалежно від того, мав місце процес нарощення грошей чи ні. Ставка відсотків може застосовуватися до однієї і тієї самої початкової суми протягом усього строку позички (прості відсоткові ставки) або до суми з нарахованими в попередньому періоді відсотками (складні відсоткові ставки). Ставка відсотків — це відсоткова ставка, яка визначається на основі початкової суми кредиту (початкова сума позички, боргу), і відсотки приєднуються в кінці окремих періодів або строку позички в цілому. Цю ставку визначають за такою формулою:
де і — ставка відсотків; Р — початкова сума боргу, кредиту, позички; n — кількість періодів нарахування відсотків або строк, на який надається позичка; S — нарощена сума або величина позички разом з нарахованими відсотками; І — відсотки за весь період позички, які визначаються за формулою I = P · i · n = S – P. Облікова ставка — це відсоткова ставка, яка визначається на основі нарощеної суми позички. Ця ставка використовується при купівлі векселів та обчислюється за такою формулою:
де d — облікова ставка. Отже, за методом нарахування відсотків розрізняють чотири види ставок: ставки відсотків та облікова ставка; прості та складні ставки відсотків.
25. Дисконтування. Сучасна вартість. Визначимо теперішню вартість капіталу, знаючи його кінцеву (майбутню) вартість. Такий процес називається дисконтуванням, а різниця між кінцевою (FV) і початковою (PV) вартістю називається дисконтом (D). Таким чином, D = FV – PV і PV можна вважати теперішньою, або здисконтованою вартістю майбутнього капіталу FV. Виходячи з того, що дисконтування є оберненою операцією до опроцентування, формули простого і складного процента застосовуються для визначення простого і складного дисконта. З формули простого процента виводиться формула простого дисконта PV1. PV1= FV1/(1 +i*n) а якщо FV1 винести за дужки, отримаємо PV1 = FV1*(1 + i · n)^(-1). (2.3.) Вираз (1 + i · n)^(-1) називається простим дисконтним множником і переважно позначається буквою vn або v. Подібно виводиться формула складного дисконта РV2. Із формули складного процента FV2 =PV(1 + i)^n маємо PV2= FV2/((1 + i)^n) а винісши FV2 за дужки, отримаємо PV2 = FV2(1 + i)^(-n). (4) Вираз (1 + i)^(-n) називається складним дисконтним множником і переважно позначається буквою vn. Виведемо ще одну формулу для визначення теперішньої вартості грошей на підставі процентної величини дисконта d. Цей показник визначається аналогічно величині процента за формулою d = D/ FV (5) При простому проценті PV1, визначається за формулою РV1 = FV1(1 + і·n)^(-1). Здисконтована вартість PV1 на підставі d буде визначатись заформулою PV1 =FV1(1 – d·n). (6) Дисконтний показник d та процентний показник і будуть відповідними, якщо обидва дадуть ту ж саму здисконтовану вартість PV вкладу (суми) FV. Тому прирівнявши формули (3) і (6) отримаємо i- d* n=1/(1+i*n) а звівши їх до спільного знаменника і прийнявши, що n = 1, маємо d=1/(1+i) i=d/(1-d) (2.7) Підставивши значення i=d/(1-d) у формулу (4), отримаємо PV2 = FV2(1 - d)^n. (8)
26. Поняття про ренту (ануїтет) і його вартість. Грошовий поток, у якому часові інтервали між двома послідовними платежами є однаковими (постійними), називають ануїтетом, або фінансовою рентою. Ануїтети можуть мати як надходження (платежі), так і витрати (виплати) коштів, тобто в них існують вхідні (зі знаком «плюс») і вихідні (зі знаком «мінус») грошові потоки. Регулярні платежі або виплати називаються членами ренти і якщо вони однакові за розмірами, то такий ануїтет називають постійним, а якщо члени різні за величиною, то ануїтет називають змінним.
За ймовірністю виплати окремого платежу ануїтети поділяються на безумовні (гарантовані) та умовні. Залежно від часу сплати (внесення) платежів (у страхуванні життя — сплати внесків) ануїтети діляться на ануїтети пренумерандо (звичайні) і ануїтети постнумерандо (приведені). Річні ануїтети — це послідовність страхових платежів або виплат, що здійснюються один раз на рік. Ренти також діляться на негайні, якщо їх виплата здійснюється безпосередньо після укладення договору, і відтерміновані (відкладені, відстрочені), якщо їх виплата розпочинається через обумовлений період після укладення договору. За тривалістю виплати розрізняють термінові (певні або конкретні), що виплачуються певну кількість часу (рік, п'ять чи десять років) і безтермінові або вічні ренти, термін виплати яких необмежений. Теперішня вартість страхових ануїтетів визначається в розрахунку на одну грошову одиницю ануїтетів постнумерандо. Інші можливі варіанти платежів — піврічні, щоквартальні і щомісячні як постнумерандо, так і пренумерандо визначаються через річні ануїтети постнумерандо.
27. Принципи обчислення фінансових рент. Розглянемо методи розрахунку нарощених сум ренти залежно від строку ренти, періодів нарахування відсотків, періодичності виплат. Використання різних методів розрахунку нарощених сум розпочнемо з річної ренти. Введемо позначення: S — нарощена сума ренти; R — розмір членів ренти; i — ставка відсотків; n — строк ренти (число років). Формула нарощеної суми річної звичайної постійної ренти:
Знайдемо сучасну величину річної ренти за такою формулою:
де А — сучасна величина ренти; an;i — коефіцієнт приведення ренти. Річна рента з нарахуванням відсотків m разів на рік.
Сучасна величина р-термінової ренти (m = 1). Якщо платежі здійснюються не один, а р разів на рік, а відсотки нараховуються один раз на рік, то коефіцієнт приведення має вигляд:
а сучасна величина ренти розраховується за формулою:
Загальний випадок знаходження сучасної величини ренти, коли відсотки нараховуються m разів, виплати відбуваються р -разів на рік, а
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 800; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.208 (0.053 с.) |
 ,
, ,
,
 ,де
,де  — коефіцієнт нарощення ренти, значення якого подаються в додатках.
— коефіцієнт нарощення ренти, значення якого подаються в додатках. ,
, .
. ,
,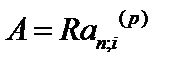 .
. :
:  .
.


